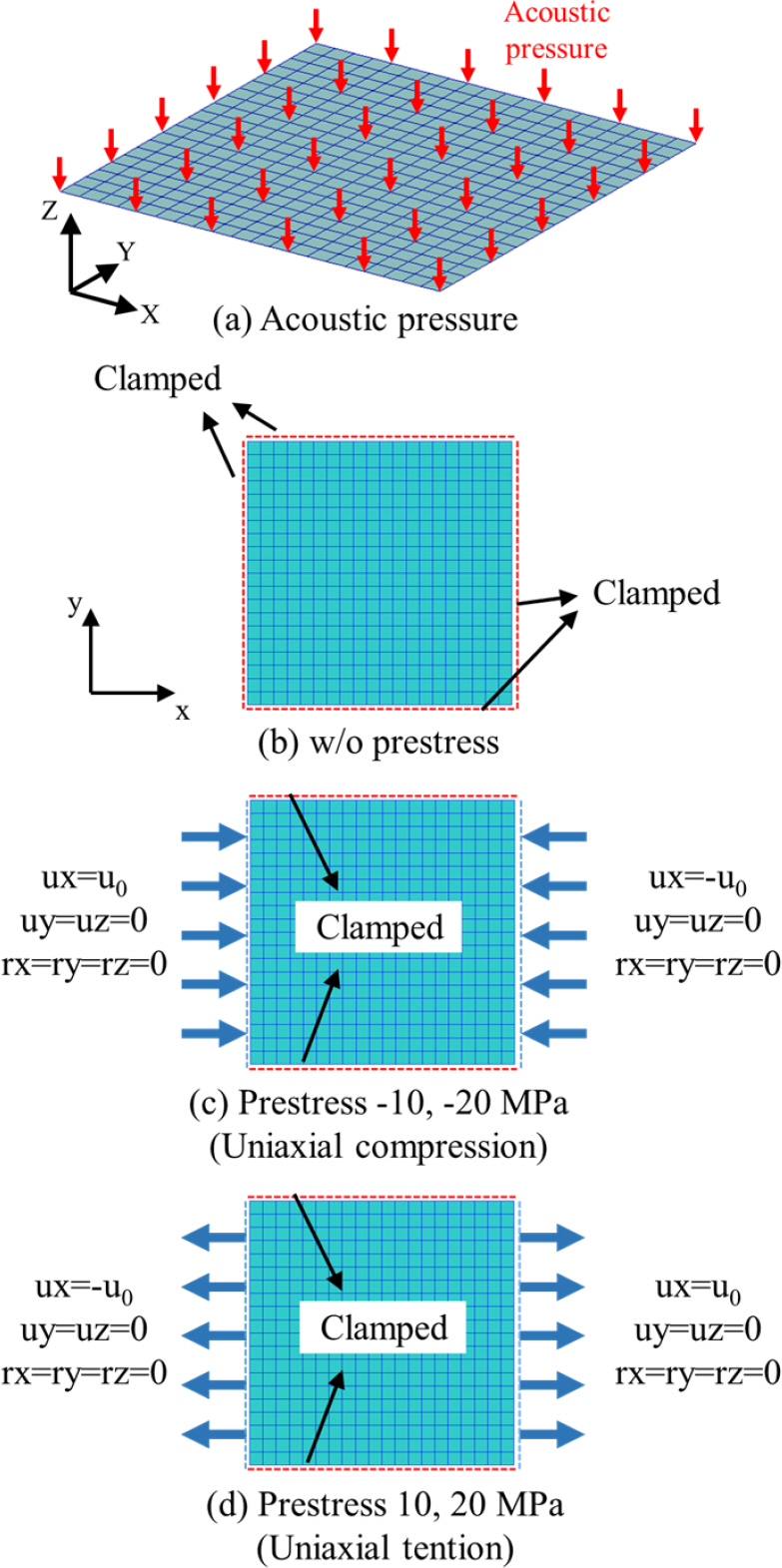
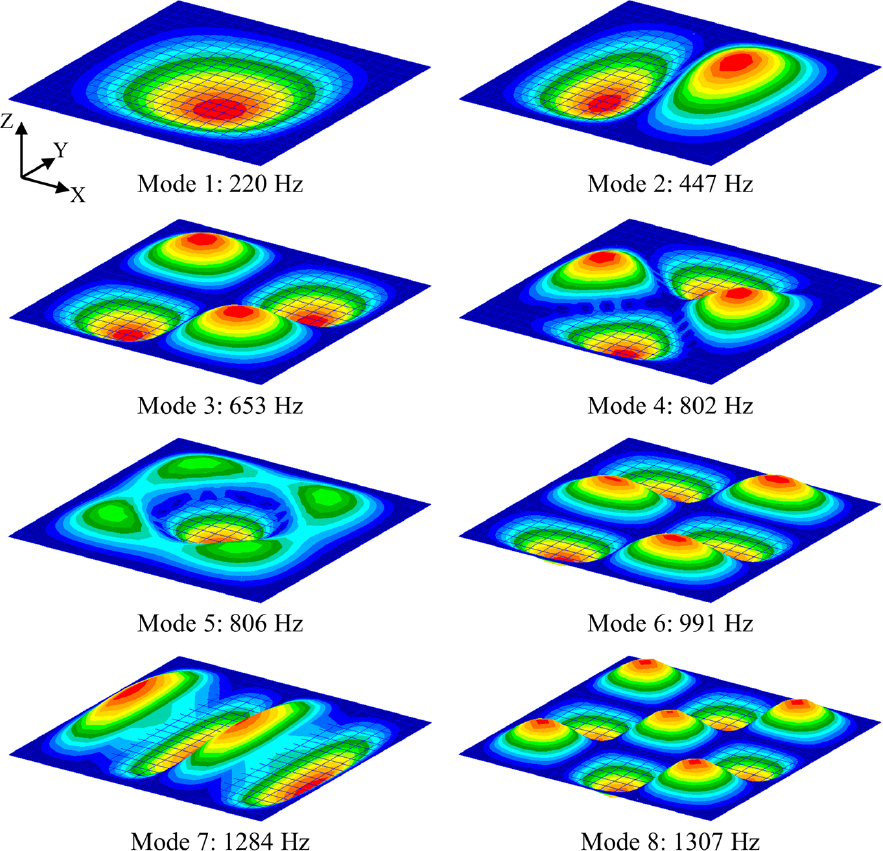
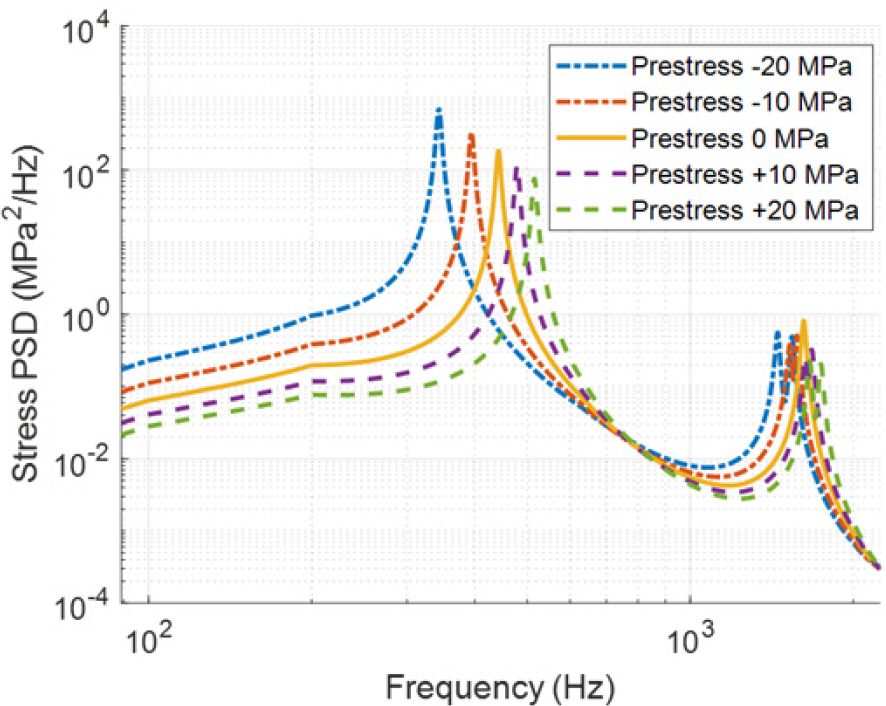
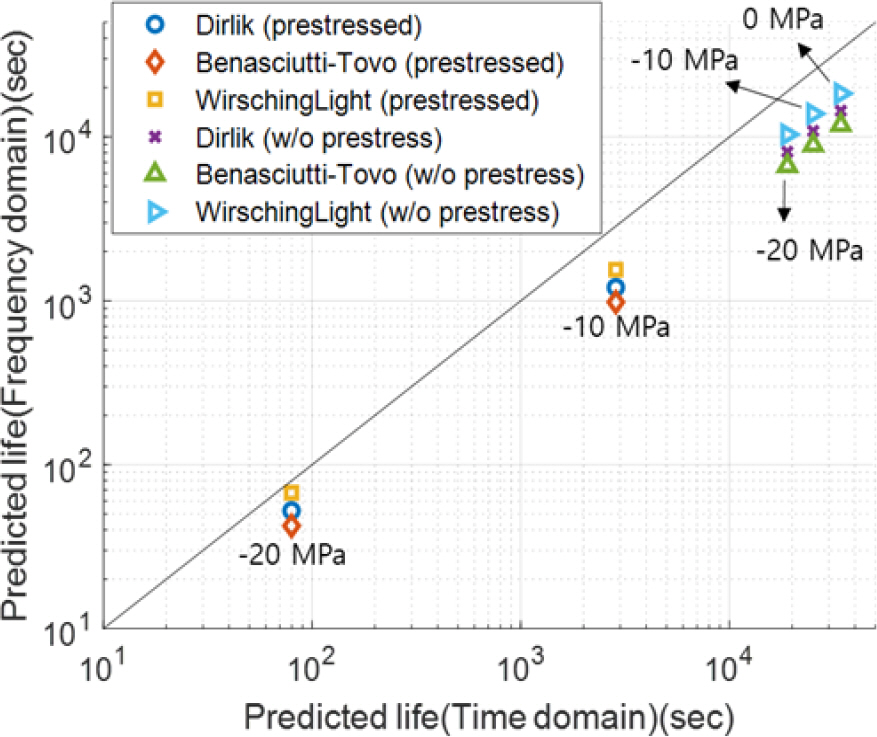
[1] Hanwha Systems. "KF-21 EO TGP," Hanwha Systems, 2022. https://www.hanwhasystems.com/kr/business/defense/isr/electronic01-tgp.do. Accessed 17 Aug 2022..
[2] R. D. Blevins, "An Approximate Method for Sonic Fatigue Analysis of Plates and Shells," Journal of Sound and Vibration, Vol. 129, No. 1, pp. 51–71, 1989.

[3] R. D. Blevins et al, "Thermo-vibro-acoustic Loads and Fatigue of Hypersonic Flight Vehicle Structure," Goodrich Aerostructures Group, Final Report, 2009.
[4] E. S. Go, M. G. Kim, I. G. Kim and M. S. Kim, "Fatigue Life Prediction in Frequency Domain Using Thermal-acoustic Loading Test Results of Titanium Specimen," Journal of Mechanical Science and Technology, Vol. 34, No. 10, pp. 4015–4024, 2020.

[5] E. S. Go, M. G. Kim, Y. S. Moon, I. G. Kim, J. S. Park and M. S. Kim, "Experimental Study on Dynamic Behavior of a Titanium Specimen Using the Thermal-Acoustic Fatigue Apparatus," Journal of Korea Society for Aeronautical and Space Sciences, Vol. 48, No. 2, pp. 127–134, 2020.

[6] M. Mršnik, J. Slavič and M. Boltežar, "Frequency- domain Methods for a Vibration-fatigue-life Estimation-Application to Real Data," International Journal of Fatigue, Vol. 47, pp. 8–17, 2013.

[7] L. Liu, Q. Guo and T. He, "Thermal-acoustic Fatigue of a Multilayer Thermal Protection System in Combined Extreme Environments," Advances in Mechanical Engineering, Vol. 6, pp. 1768912014.

[8] MIL-STD-810G. "Environmental Engineering Considerations and Laboratory Tests," US Department of Defense, 2008.
[9] H. S. Jung, K. S. Kim, J. S. Kim and S. W. Lee, "Fatigue Life Evaluation in Frequency Domain of Aircraft Equipment Exposed to Random Vibration," Journal of Korea Society for Aeronautical and Space Sciences, Vol. 45, No. 8, pp. 627–638, 2017.

[10] O. C. Jun and S. Kim, "Design of Instrumented Pod for Flight Aeroacoustic Environment," Journal of Korea Society for Aeronautical and Space Sciences, Vol. 40, No. 6, pp. 536–541, 2012.

[11] J. M. Cho, J. Jang, W. C. Choi and J. I. Bae, "Fatigue Life Prediction of Sensor Pod for Aircraft Considering Aircraft Loads," Journal of Aerospace System Engineering, Vol. 13, No. 3, pp. 32–39, 2019.
[12>] A. Niesłony and M. Böhm, "Frequency-Domain Fatigue Life Estimation with Mean Stress Correction," International Journal of Fatigue, Vol. 91, pp. 373–381, 2016.

[13] E. S. Go, I. G. Kim, M. H. Jeon, H. J. Cho, J. A. Park and M. S. Kim, "Generation of Time Series Data from Octave Bandwidth SPL of Acoustic Loading Using Interpolation Method," Journal of the Korea Institute of Military Science and Technology, Vol. 24, No. 1, pp. 1–11, 2021.

[14] P. H. Wirsching and M. C. Light, "Fatigue under Wide Band Random Stresses," Advances in Mechanical Engineering, Vol. 106, No. 7, pp. 1593–1607, 1980.

[15] T. Dirlik, Application of Computers in Fatigue Analysis, Ph.D. Thesis, University of Warwick. 1985.
[16] R. Tovo, "Cycle Distribution and Fatigue Damage under Broad-band Random Loading," International Journal of Fatigue, Vol. 24, No. 11, pp. 1137–1147, 2002.

[17] D. Benasciutti and R. Tovo, "Spectral Methods for Lifetime Prediction under Wide-band Stationary Random Processes," International Journal of Fatigue, Vol. 27, No. 8, pp. 867–877, 2005.

[18] N. Dowling, "Fatigue Failure Predictions for Complicated Stress-Strain Histories," Journal of Materials, Vol. 7, No. 1, pp. 71–87, 1972.

[19] J. Goodman, "Mechanics Applied to Engineering," Longmans, Green, 1919.
[20] V. Adams and A. Askenazi, "Building Better Products with Finite Element Analysis," OnWord Press, 1999.
[21] MIL-HDBK-5H. "Metallic Materials and Elements for Aerospace Vehicle Structures," US Department of Defense, 1998.