서 론
위성용 EO/IR 탑재체는 위성에 탑재되는 전자광학 장비를 말하며, 물체가 반사하거나 복사하는 가시광선 및 적외선 대역의 전자기파를 감응하여 영상을 획득하는 장비이다. 본 논문 제목의 다중대역광학센서는 EO(Electro-optic)/IR(Infrared)의 전 파장대역 중에서 다양한 파장대역의 영상을 동시에 제공하는 센서를 의미한다. 따라서 광범위한 표적에 대한 온도 정보 획득이 가능하며 안개, 미세먼지 등의 기상 상황에 상대적으로 우수한 영상정보 획득이 가능하다[1].
하지만 위성용 광학센서의 조립과 정렬이 이루어지는 지상 환경은 우주 환경과 달리 중력이 존재하므로 중력에 의해 발생하는 광학 성능 저하량 분석은 필수적이며, 중력으로 인한 파면오차 버짓을 만족해야 한다. 따라서 본 논문에서는 구조 건전성을 확보한 다중대역광학센서 광구조체에 대해 중력에 의한 각 광학품의 무게 중심 이동량을 구조해석을 통해 산출하였으며, 광학 민감도와 함께 파면오차 발생량을 계산하였다[2-4]. 분석 결과, 중력에 의해 발생하는 파면오차 발생량이 대역별 파면오차 버짓을 만족하지 못하는 것을 확인하였으며, 파면오차를 최소화하기 위한 자중 보상 기법을 고안하였다. 대상의 운용 환경이 중력이 존재하지 않는 우주일 경우, 필요에 따라 중력을 보상하기 위한 기법이 적용되어 왔으며[5-7], 본 논문에서는 경통 앞단에 보상 하중을 가함으로써 가장 민감한 부 반사경의 위치를 중점적으로 조정하여 파면오차를 효과적으로 줄이는 보상 기법을 소개하였다.
본 논문의 2장에서는 다중대역광학센서의 광학 설계와 함께 구조 설계 개념을 소개한 후, 중력 환경에 대한 파면오차 버짓을 기술하였다. 3장에서는 다중대역광학센서 광구조체의 유한요소모델에 대한 구성과 함께 구조해석 방법을 서술하였으며, 중력에 의해 발생하는 파면오차 발생량을 계산하였다. 4장에서는 중력으로 인해 발생하는 대역별 파면오차를 줄이기 위한 자중 보상 기법의 개념에 대해 소개하였으며, 보상 위치와 보상 하중에 따른 파면오차 변화량을 분석하여 적절한 보상 위치와 하중을 결정하였다. 마지막으로 자중 보상 기법을 적용하지 않았을 때와 적용하였을 때의 파면오차 발생량을 대역별로 비교하여 자중 보상의 효과를 서술하였다.
다중대역광학센서 구조설계
2.1 다중대역광학센서 설계 개념
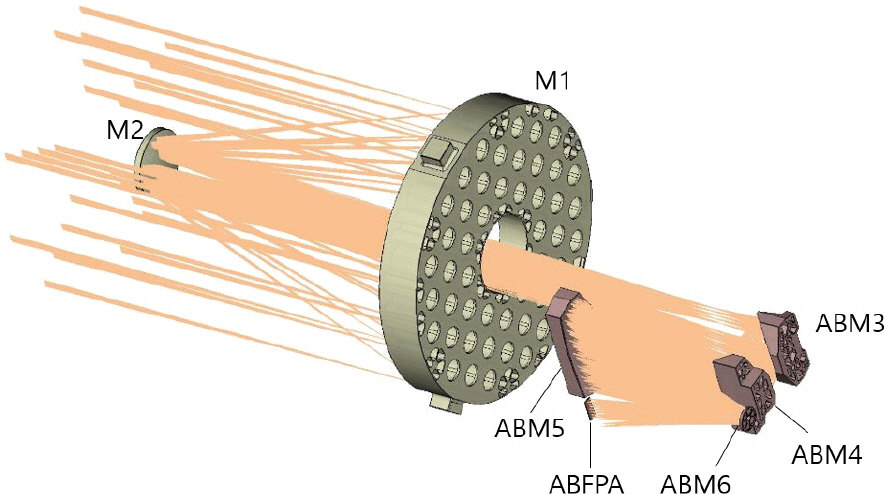
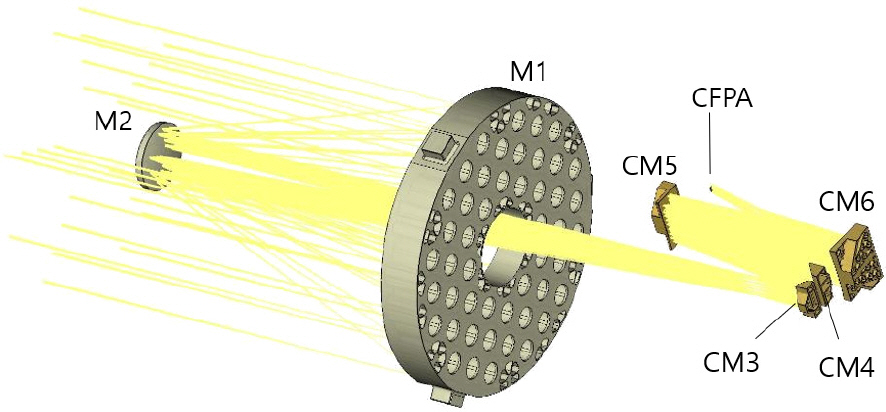
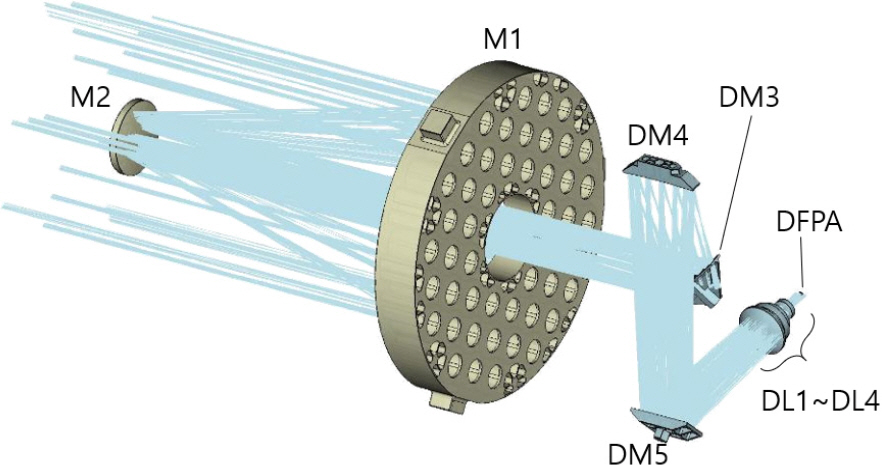
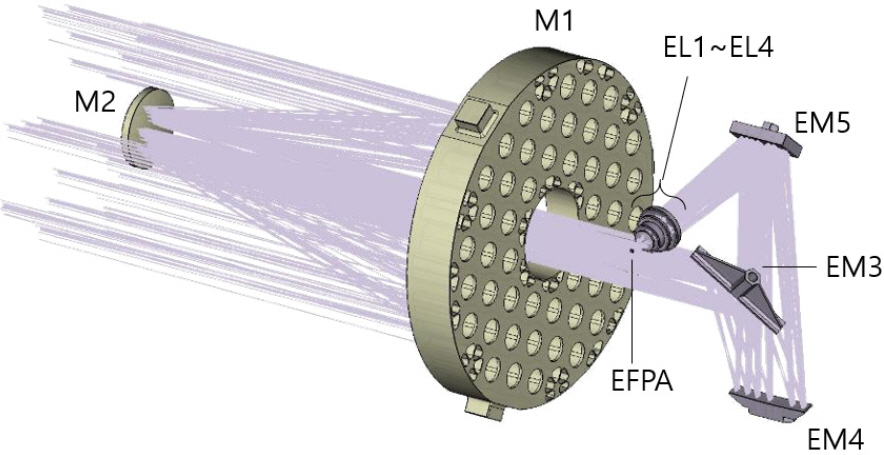
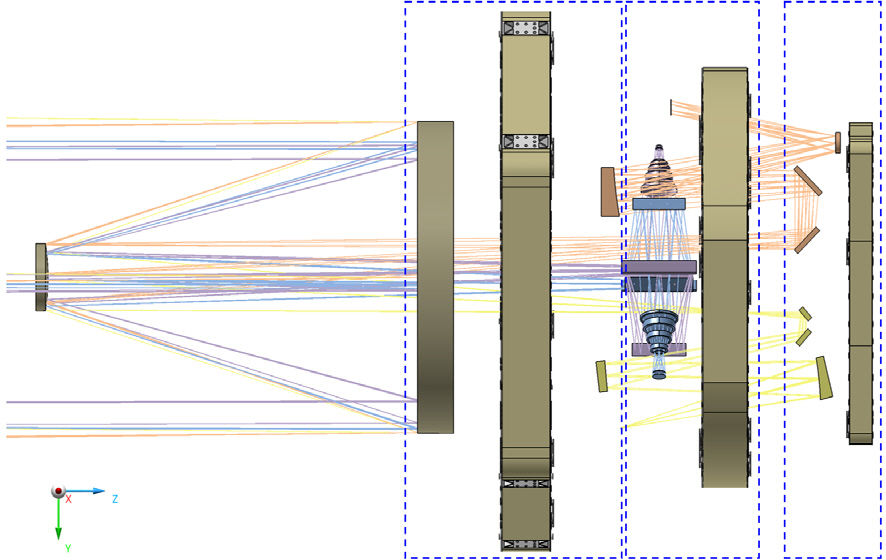
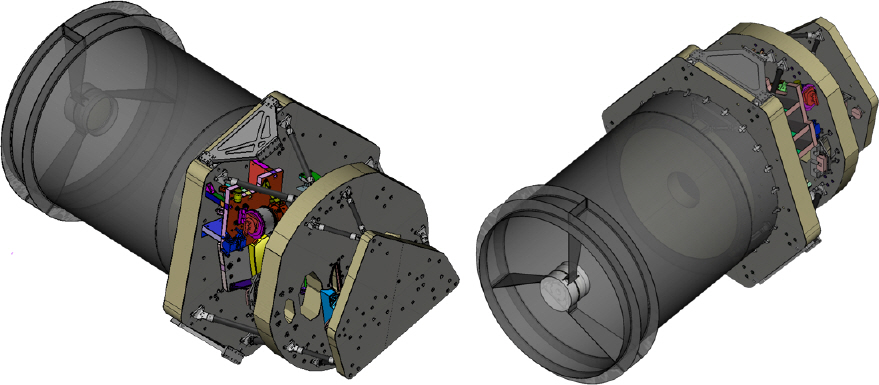
다중대역광학센서는 위성용 탑재체로써 목표물에 대한 보다 자세한 정보를 제공하기 위해 여러 개의 파장대역의 영상을 동시에 제공하는 EO/IR 광학 센서이다. 본 논문에서 다루는 다중대역광학센서는 A, B, C, D, E 대역의 5개의 파장 대역을 갖으며, Fig. 1과 같은 형상으로 설계되었다. 공통 광학계인 주 반사경과 부 반사경을 통해 광선 다발을 모으고, 중간 상면 부근에서 시야각에 따라 분리시켜 각 대역별 검출기에 상을 맺을 수 있도록 광학계를 설계하였다. 단, A 와 B 대역은 광학계를 공유하면서 동일 상면에서 검출기의 영역을 나누어서 대역을 분리하였다. A/B 대역은 Fig. 2와 같이 공통 광학계인 주 반사경 M1과 부 반사경 M2를 통과 후 ABM3, ABM4, ABM5, ABM6 네 개의 거울면에 차례로 반사되어 검출면에 도달한다. C 대역은 Fig. 3과 같이 광선이 M1과 M2를 통과 후 CM3, CM4, CM5, CM6의 네 개의 거울면을 거쳐 검출면에 도달한다. D 대역과 E 대역은 A/B, C 대역과 다르게 렌즈 광학계가 추가된다. D 대역과 E 대역은 각각 Fig. 4와 Fig. 5 같이 세 개의 거울면과 네 개의 렌즈를 통과한 빛이 검출면으로 입사된다.
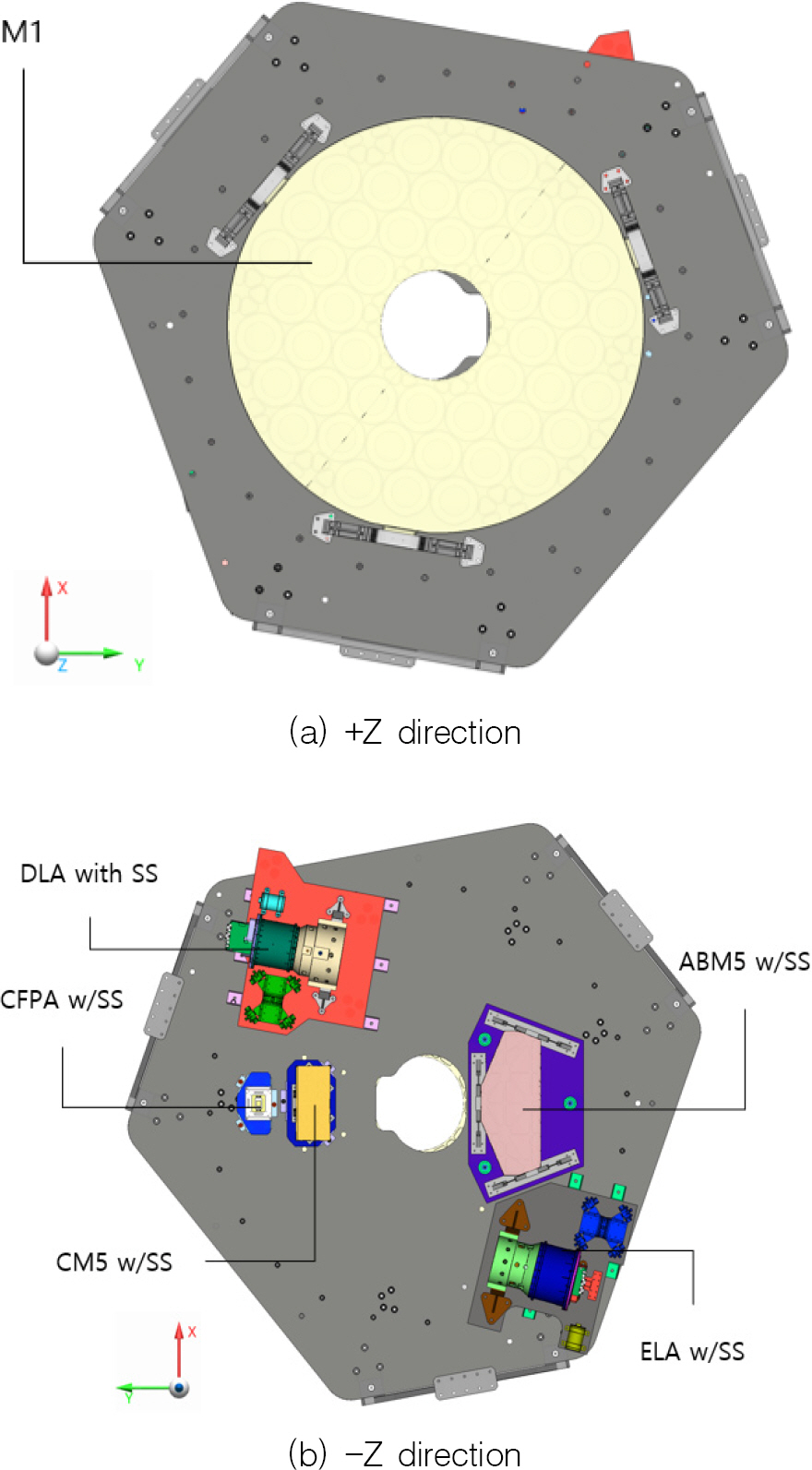
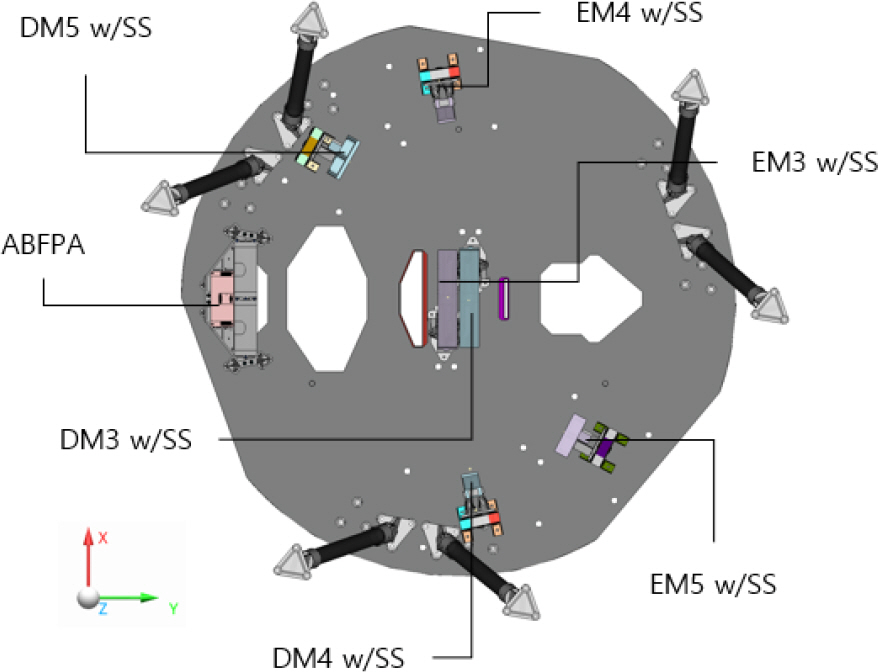
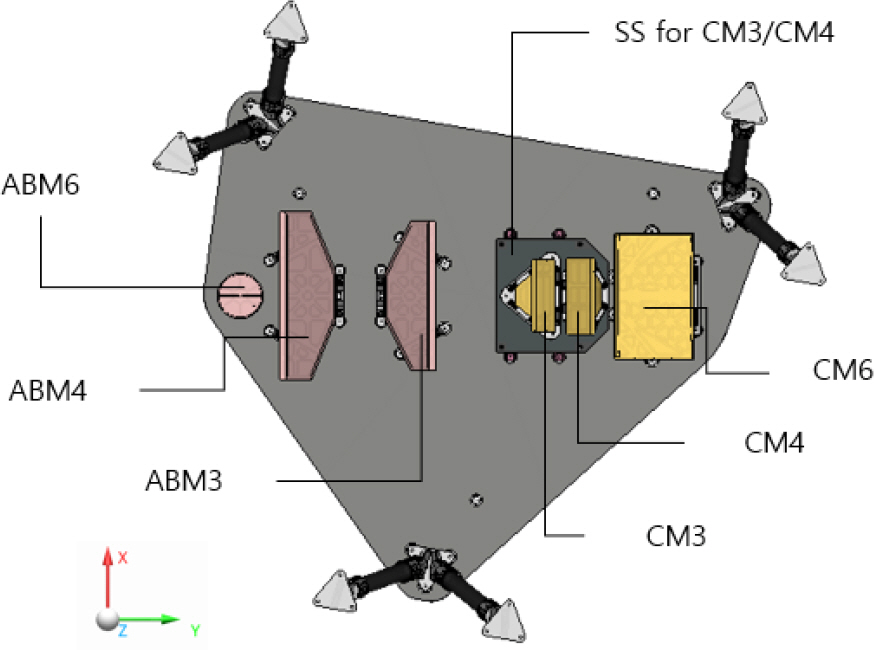
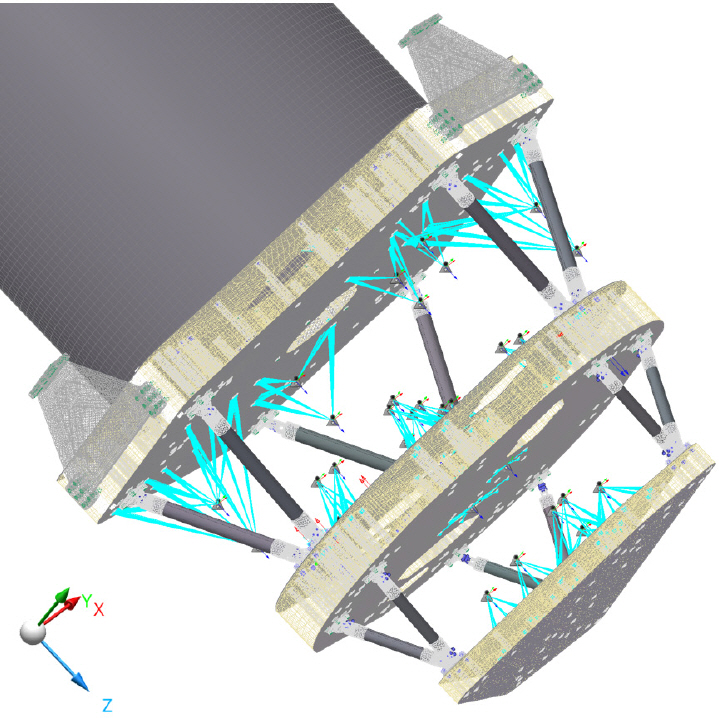
확정된 광학 설계를 바탕으로 5개의 대역을 구성하는 반사경 16종, 렌즈 8종, 검출기 조립체를 제한된 공간 내에서 효율적이면서 광학적/기계적 간섭이 발생하지 않고, 원활한 조립/정렬 작업이 이루어지기 위한 구조설계를 수행하였다. Fig. 6에서 볼 수 있듯이 경통 앞단에 있는 부 반사경을 제외한 구성품들은 Z축 위치를 기준으로 크게 3구역으로 나누어서 배치할 수 있다. 이에 3개의 베젤에 구성품들이 장착되도록 다층 구조의 컨셉으로 구조설계를 진행하였으며, 각 베젤은 bipod 형태의 트러스로 지지된다. 모든 반사경과 렌즈는 발사 하중과 열 하중으로 인한 광학면 변형을 최소화하기 위한 플렉셔라는 구조와 함께 베젤에 장착된다[8]. 추가로 C 대역의 M3, M4 반사경과 같이 베젤로부터 거리가 있거나 D, E 대역의 M3, M4, M5 반사경과 같이 광학면이 베젤과 수직을 이루는 구성품들은 지지구조물(SS; Support Structure)과 함께 베젤에 장착되도록 하였다[9]. 결과적으로 M1 베젤의 +Z 면에는 주 반사경이, M1 베젤의 –Z 면에는 A/B 대역과 C 대역의 M5 반사경과 D, E 대역의 렌즈조립체, C 대역의 검출기가 장착되며 Fig. 7에 나타내었다. D, E 대역의 M3, M4, M5 반사경과 A/B 대역의 검출기는 Fig. 8과 같이 DE 베젤에 장착되며, 마지막으로 A/B 대역의 M3, M4, M6 반사경과 C 대역의 M3, M4, M6 반사경은 Fig. 9와 같이 ABC 베젤에 장착되도록 배치하였다. Fig. 10은 세 층으로 구성된 다층 베젤 구조를 가지는 다중대역광학센서의 광구조체 최종 형상이다.
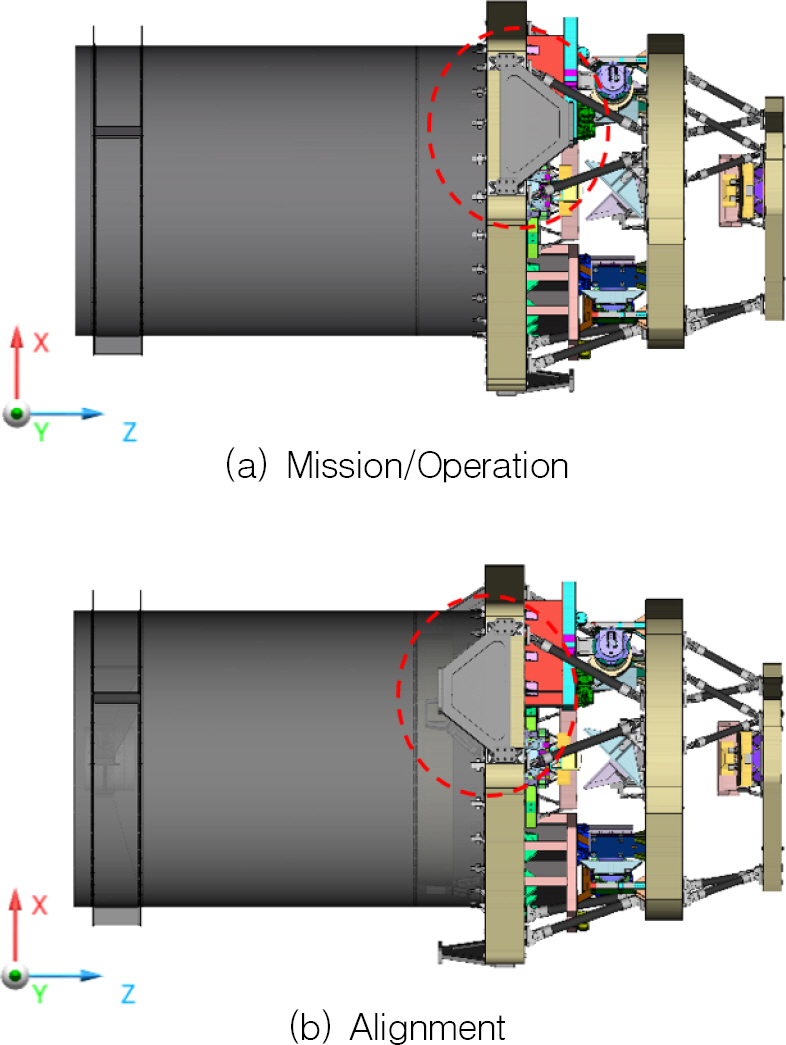
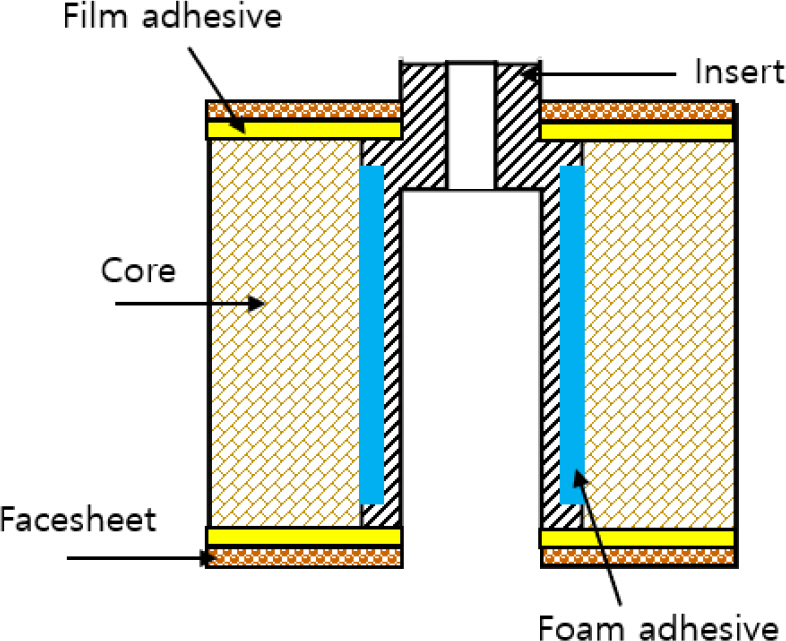
Telescope flexure(탑재체 지지대)는 Fig. 11의 (a)와 같이 M1 베젤에 장착되어 다중대역광학센서와 위성체 플랫폼을 연결하는 역할을 하며, 모든 구성품의 기준이 되는 M1 베젤 평면의 변형을 최소화하도록 설계되었다. 하지만 Fig. 11의 (a)의 형상으로 조립/정렬/측정을 할 경우, M1 베젤과 DE 베젤 사이에 위치하는 광학조립체에 대한 작업성에 매우 큰 불편을 초래한다. 이를 해소하기 위해 지상에서 조립/정렬/측정 시에는 telescope flexure를 Fig. 11의 (b)와 같이 Z축 기준 반대 방향으로 장착하여, 지상지원장비와 광학조립체 작업공간 간의 간섭을 최소화하였다. Telescope flexure의 장착 방향에 따른 성능변화는 무시할 수준임을 확인하였다. 각 베젤은 CFRP(Carbon Fiber Reinforced Plastics) 소재의 facesheet와 알루미늄 허니콤 코어로 구성된 샌드위치 패널의 구조로 이루어져 있으며[10], 허니콤 코어에는 Fig. 12와 같이 광학 조립체와 검출기 조립체, 트러스를 조립하기 위한 알루미늄 재질의 인서트가 삽입되어 있다.
다중대역광학센서의 광구조체는 위성 발사 및 궤도 환경에서 구조 건전성을 가지도록 강성과 강도를 고려하여 설계되었다. 강성은 구조체 간 공진주파수를 이격하기 위한 목적으로, 모드 해석을 통해 고유진동수를 확인함으로써 설계 요구 조건 만족 여부를 확인하였다. 강도는 발사, 궤도 환경에서 파손을 방지하기 위한 목적으로 설계지표로 사용되었으며, 설계하중과 열 하중에 대한 정적하중 해석을 수행하여 안전여유 (MOS; Margin of safety)를 계산함으로써 검증하였다. 다중대역광학센서의 고유진동수 요구조건은 발사체에서 요구하는 위성체의 최소 고유진동수를 고려하였고, 위성체 고유진동수와 이격시키기 위한 octave rule[11]을 적용하여 도출하였다. 위성체의 최소 고유진동수는 발사체 설명서에서 찾을 수 있으며, 본 연구에서는 설계 초기 단계로 발사체 후보 중 조건이 가장 가혹한 발사체를 기준으로 설계 요구조건을 도출하였다. Table 1에 강성과 강도에 대한 요구 조건을 정리하였다.
2.2 중력 환경에 대한 파면오차 버짓
다중대역 광학센서의 광구조체는 앞에서 설명한 구조건전성 뿐만 아니라, 발사 및 궤도 환경에서 광학 성능을 만족하도록 설계되어야 한다. 발사 시 진동/충격으로 인한 영향과 궤도에서 운용 중 열로 인한 영향, CFRP에서 수분이 빠져나가는 영향 그리고 중력으로 인한 광학 성능 저하를 고려하였다.
본 논문에서는 강성과 강도 요구 조건을 모두 만족하여 구조 건전성을 확보한 다중대역광학센서의 광구조체에 대하여 4개의 환경요인 중 중력으로 인한 구조체 변형과 이에 따른 광학 성능 저하량을 분석하였으며, 이때 광학 성능을 확인하기 위한 성능지표로는 파면오차를 사용하였다. 광구조체는 각 대역별 간섭계를 이용하여 파면오차를 최소로 만들도록 조립과 정렬이 이루어진다. 하지만 지구 중력에 의해 광구조체가 변형된 상태에서 모든 조립과 정렬이 이루어지기 때문에, 중력에 의해 발생하는 파면오차 또한 함께 제거되어 정렬된다. 이후 우주로 발사된 후에는 중력이 사라지면서 중력에 의해 변형되었던 구조가 다시 제자리로 돌아오고, 제거되었던 파면오차가 다시 발생하게 된다. 따라서 중력에 의해 발생하는 광학 성능 저하량 분석이 필수적이며, Table 2에 각 대역별 중력으로 인한 파면오차 버짓을 정리하였다.
자중에 의한 구조 변형 및 광학 성능 영향 분석
3.1 해석 조건
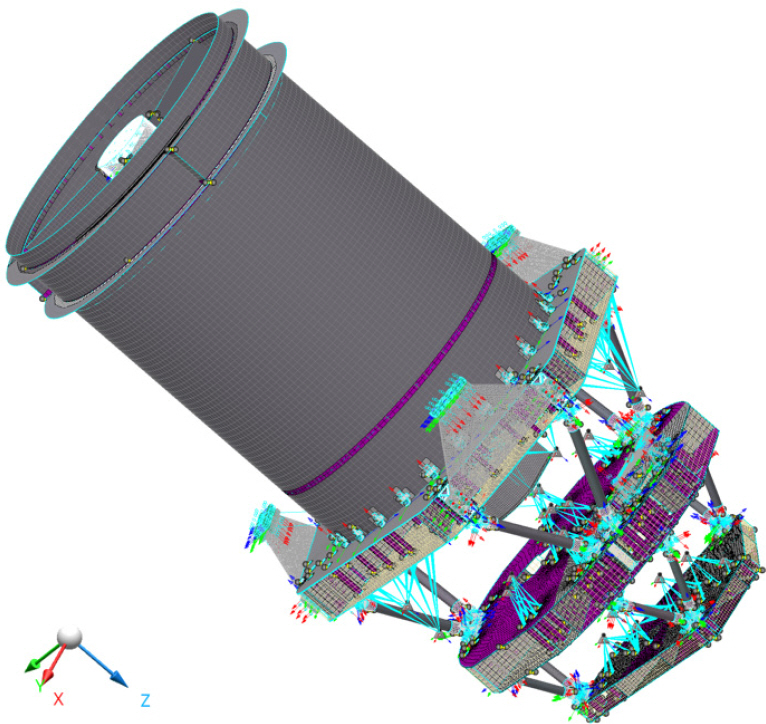
유한요소모델 구성 및 해석에는 MSC 계열의 소프트웨어를 사용하였다. 먼저 Apex를 활용하여 geometry 모델 구성, mesh 구성, 경계조건 설정, 해석 조건 설정 등의 전처리 과정을 수행하였다. 이후 솔버인 MSC Nastran을 통해 각종 해석을 수행한 다음, MSC Patran 을 활용하여 후처리 과정을 수행하였다. 구성한 다중대역광학센서의 유한요소모델을 Fig. 13에 나타내었으며, Table 3과 같이 구성하였다. 구조해석에 사용된 global 좌표계의 Z축은 광축 방향이며, X축은 AB 대역과 C 대역의 M3, M4, M6 반사경이 놓인 축으로 정의하였다. 다중대역광학센서에 대한 유한요소모델은 CFRP 적층으로 구성된 베젤의 facesheet와 트러스의 tube, 경통 등은 shell 요소로 구성하였고, 그 외 파트는 solid 요소로 구성하였다. 해석 결과에 큰 오차가 생기지 않으면서도 효율적인 해석을 수행하기 위해, 각 하위 조립체 별 모드해석 결과인 고유진동수의 값이 수렴하고, 국부적인 응력 집중이 발생하지 않도록 격자 크기를 결정하였다.
Table 3.
Finite element model information
반사경/렌즈와 플렉셔로 구성된 각 광학 조립체, 검출기 조립체, 지지구조물은 유한요소모델 상에 Fig. 14와 같이 질점(point mass)으로 구성하였다. 각 질점의 위치와 질량은 설계된 각 광학 조립체, 검출기 조립체, 지지구조물의 무게 중심과 질량으로 반영하였으며, 질점의 정보를 Table 4에 정리하였다. 주 반사경과 부 반사경을 제외한 광학 조립체들은 크기와 질량이 작고, 광학적 민감도도 작으므로 해석에 필요한 계산 비용을 줄이기 위해 플렉셔를 포함한 광학 조립체 단위를 질점으로 구성하였다. 반면 크기와 질량이 크고 광학적으로 매우 민감한 주 반사경 조립체와 부 반사경 조립체의 경우, 플렉셔의 변형을 함께 고려하여 중력으로 인한 변형량의 해석 정확도를 높이고자 플렉셔를 solid 요소로 구성하였다. 질량이 큰 주 반사경을 solid 요소로 적용하지 않은 이유는 중력으로 인한 주 반사경 조립체의 변형에 가장 큰 영향을 끼치는 원인은 베젤 구조체의 변형과 주 반사경을 지지하고 있는 3개의 유연한 플렉셔의 변형이며, 미러 자체의 광학면 변형은 플렉셔가 흡수해주고 있기 때문이다. Fig. 15와 Fig. 16은 각각 주 반사경 조립체와 부 반사경 조립체의 유한요소모델을 보여준다. Table 4에 표시하였듯이 M2, 지지구조물을 포함한 AB 대역과 C 대역의 M5 광학 조립체와 검출기 조립체는 보상자로 사용되는 구성품으로써 조립/정렬 단계의 마지막에 베젤에 장착되기 때문에 질량을 0으로 설정하였다.
Table 4.
Point mass information
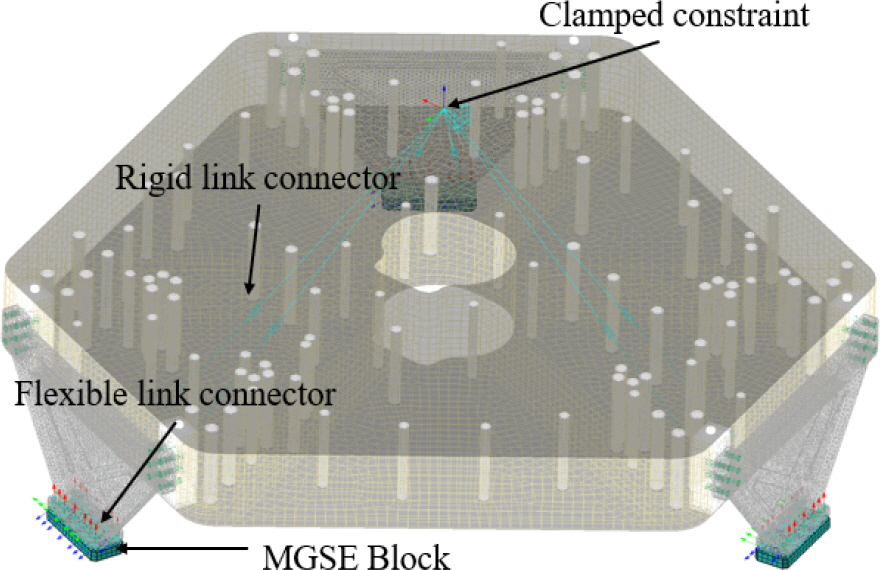
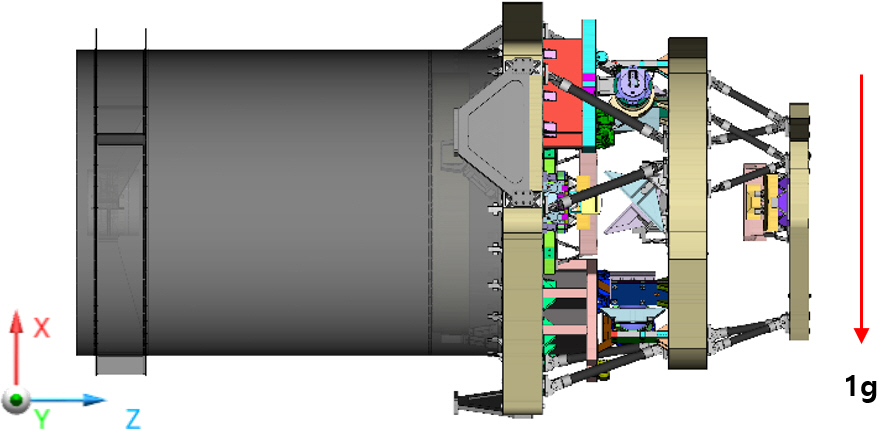
유한요소모델 상에서 파트 간 연결 방법은 크게 접착부와 체결부로 구분된다. 먼저 본드를 사용하는 접착부의 경우 MSC Apex에서 mesh independent tie 기능을 활용하여 BCONECT 방식으로 구현하였으며[12], facesheet와 코어, 인서트와 코어, 코어와 코어 사이 등에 적용하였다. 볼트를 사용하는 체결부의 경우 node tie와 flexible link 방식의 connect 기능을 이용하여 RBE2-CBAR-RBE2 방식으로 구현하였고, 트러스와 베젤 사이의 연결부, 인서트와 telescope flexure 사이의 연결부 등에 적용하였다. 경계조건은 Fig. 17과 같이 설정하였다. 먼저 위성체 플랫폼 또는 기계지상지원장비(MGSE; mechanical ground support equipment) 등의 외부와 연결되는 telescope flexure의 외부 인터페이스 강도 분석을 위해 모델에 기계지상지원장비를 모사하는 블록을 추가하였다. Telescope flexure 하단 체결부와 블록 간에는 Flexible link connector로 연결하였으며, 블록은 충분히 rigid한 특성을 갖도록 탄성계수를 조정하였다. 3개의 블록 중심에는 Clamped 조건의 6자유도 변위 구속인 질점을 생성하고, 이 질점과 각 블록은 Rigid link connector로 연결하였다. 해석 조건은 Fig. 18과 같은 조립/정렬 형상에서 중력 방향인 X 축 방향으로 1 g를 부여하였다.
3.2 해석 결과
중력에 의해 발생하는 파면오차를 계산하기 위해서는 광학 조립체의 이동량과 광학 민감도 정보가 필요하다. 구조해석을 통해 다중대역광학센서의 다층 구조물이 중력에 의해 변형되면서 발생한 광학 조립체의 무게 중심 이동량을 산출하였다. 광학 민감도란 다중대역광학센서의 모든 광학품에 개별적으로 미소 변위를 가했을 때 발생하는 단위 변위 당 파면오차 발생량을 의미한다. 광학 설계 프로그램인 CODE V에서 분석한 광학 민감도와 구조해석을 통해 산출한 무게 중심 이동량을 곱하여 그로 인한 파면오차 발생량을 분석하였다[2-4].
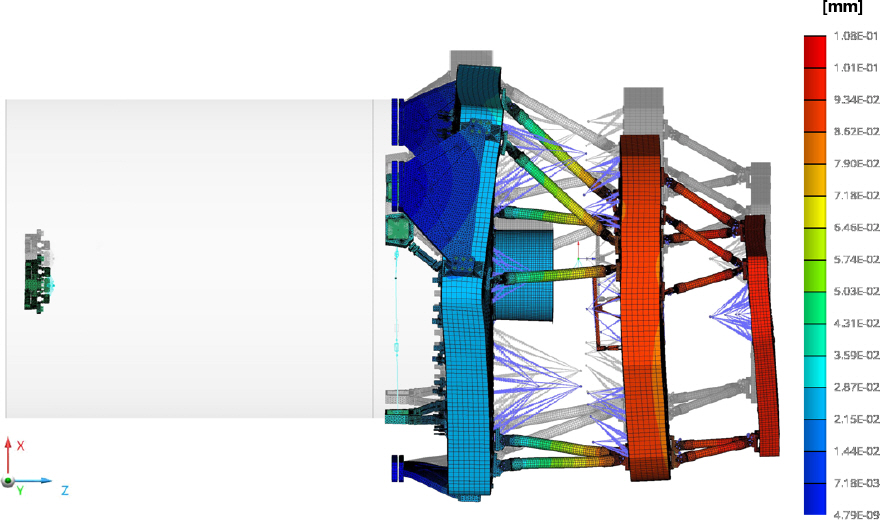
Fig. 19는 다중대역광학센서 광구조체의 조립/정렬 형상에서 중력 방향인 X축 방향으로 1 g를 부여하였을 때, 변형되는 형상을 보여준다. 흑백으로 나타낸 형상이 변형 전 형상이며, 컬러로 나타낸 형상이 변형 후 형상이다. 부 반사경의 변형 후 위치를 잘 보이기 위해 경통의 변형 후 형상은 보이지 않았다. Table 5에 구조해석을 통해 계산된 광학 조립체 무게 중심의 이동량을 구조해석에서 사용된 global 좌표계 기준으로 병진 방향과 회전 방향에 대해 각각 정리하였다.
Table 5.
Displacement of point mass under 1 g
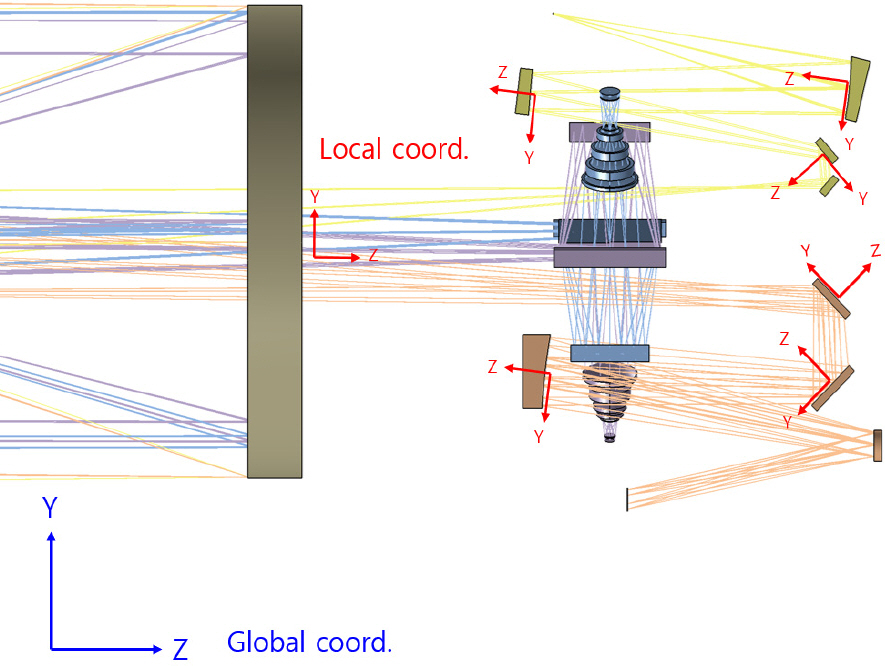
한편, 구조해석과 광학해석 결과의 좌표계가 다르기 때문에 global 좌표계에서 계산된 이동량을 각 광학품의 local 좌표계로 변환하였으며, Fig. 20에 구조해석에서 사용된 global 좌표계와 각 광학품의 local 좌표계를 표시하였다. Local 좌표계의 Z축은 각 광학면의 수직 방향으로 정의되며, X, Y축은 광학면의 수평 방향으로 정의된다. Local 좌표계로 변환된 각 광학 조립체의 이동량과 광학 민감도 분석 결과를 이용하여 파면오차 발생량을 분석하였으며, 분석 결과를 Table 6에 정리하였다. A/B 대역의 경우, 조립/정렬 형상에서 중력으로 인해 16.40 nm rms의 파면오차가 발생하는 것으로 분석되며, 이는 할당된 10 nm rms 이하의 요구 조건을 충족시키지 못하게 된다. 따라서 중력으로 인해 발생하는 대역별 파면오차를 줄이는 방안이 필수적이며, 이에 자중 보상 기법을 고안하였다.
자중 보상 기법 적용을 통한 광학 성능 향상
4.1 자중 보상 기법 개념
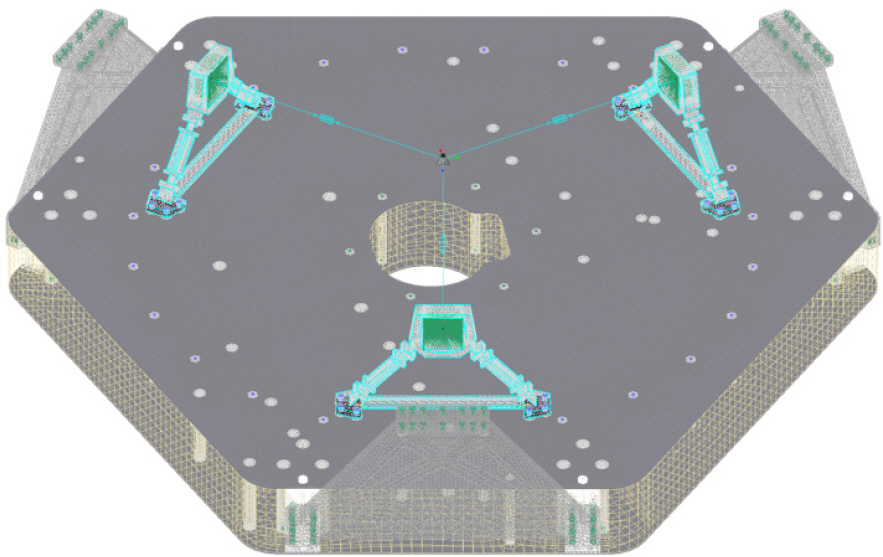
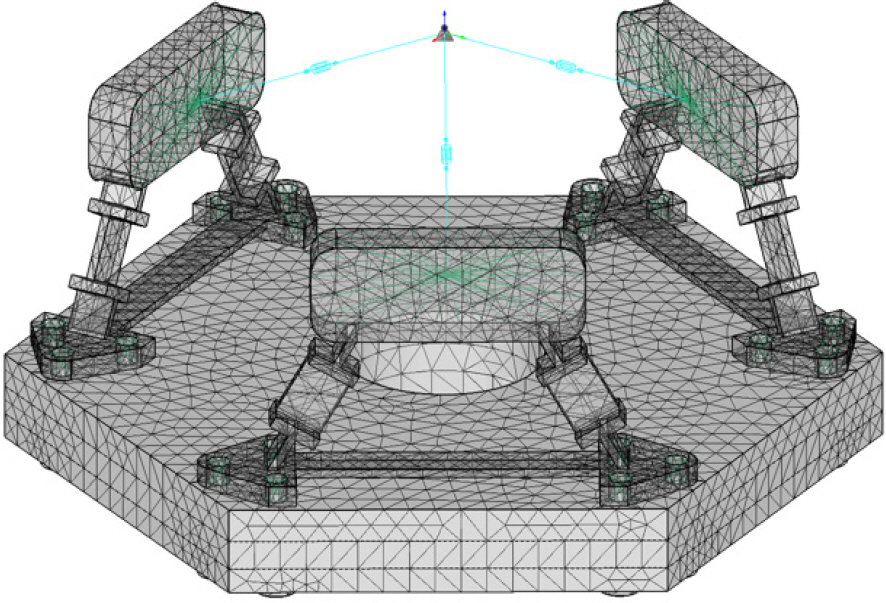
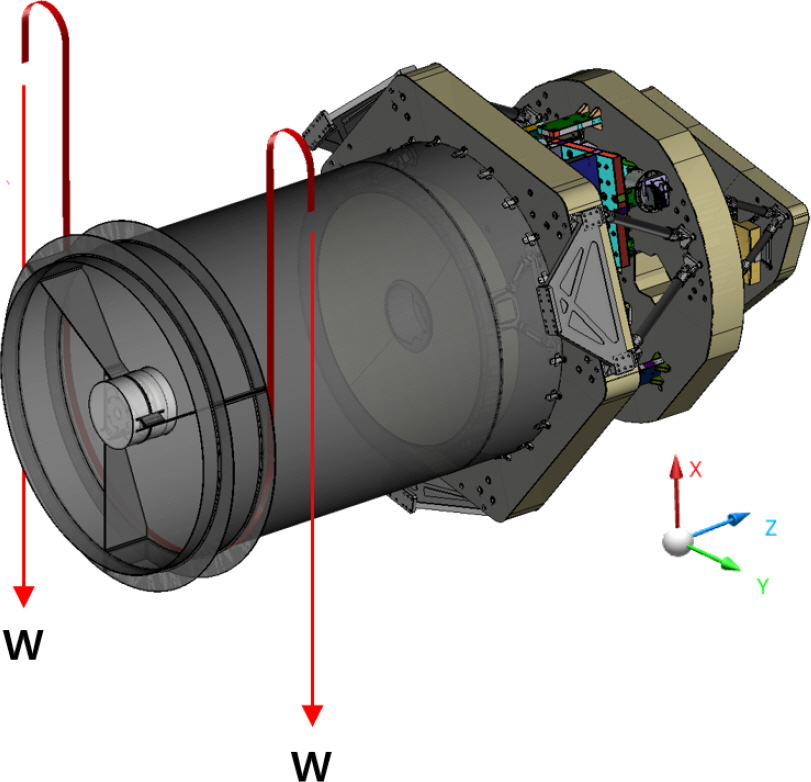
다중대역광학센서는 다수의 반사경, 렌즈, 검출기로 구성되어있으며, 수많은 구성품이 받는 중력을 각각 보상하는 것은 시간과 비용적인 면에서 비현실적인 방법이다. 따라서 본 논문에서는 경통 앞단에 보상 하중을 가하는 자중 보상 기법을 적용하였다. 이 기법은 특히 광학적으로 가장 민감하면서 조립/정렬 방향에서 변형이 많이 일어나는 경통 앞단에 위치한 부 반사경의 위치를 중점적으로 조정함으로써 중력으로 인한 파면오차를 효과적으로 줄일 수 있다. Fig. 21에 본 연구에서 적용한 자중 보상 방안을 도식화하였다. 4.2절에서는 보상 위치별 보상 하중에 따른 광학 성능을 분석하여 자중 보상 기법을 적용할 세부 위치와 최적의 보상 하중을 결정하였다.
4.2 보상 위치와 하중에 따른 광학 성능 분석
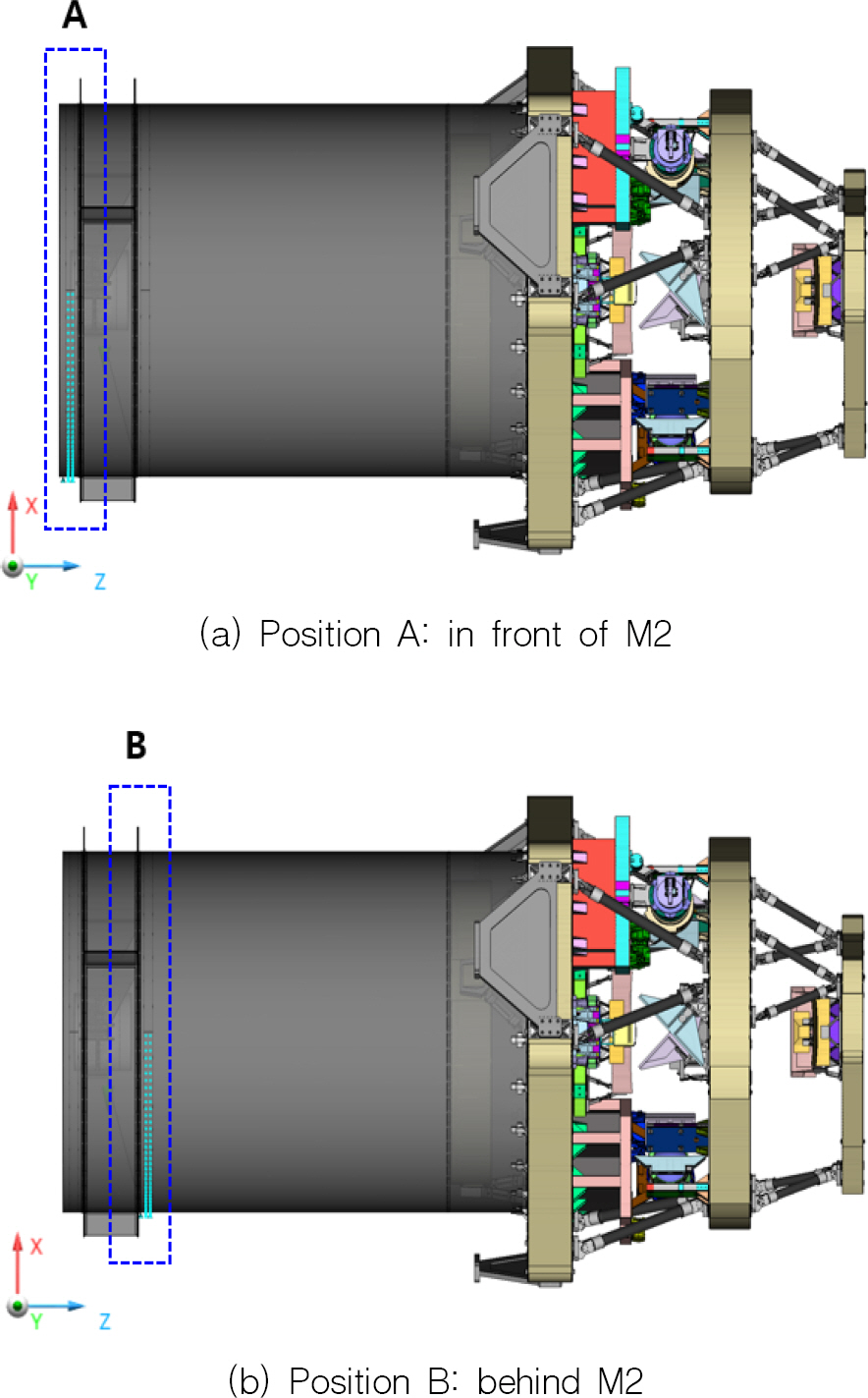
자중 보상 적용 위치를 결정하기 위해 Fig. 22의 (a), (b)와 같이 부 반사경 앞과 뒤에 각각 자중보상장치를 적용하여 각 질점이 이동하는 양을 구조해석을 통해 산출하였다. 동일한 적용 보상 위치에서 보상 하중에 따른 각 질점의 이동량은 비례하므로 단위 하중 당 발생하는 질점의 이동량을 계산하였다. Reinforce ring을 기준으로 각각 반대 방향으로 동일한 거리에 떨어진 위치인 A와 B에 하중을 부여하여 질점의 이동량을 계산하였으며, 그 결과를 Table 7과 Table 8에 각각 정리하였다.
Table 7.
Displacement of point mass according to the unit load under 1 g with gravity compensation equipment(position: A)
Table 8.
Displacement of point mass according to the unit load under 1 g with gravity compensation equipment(position: B)
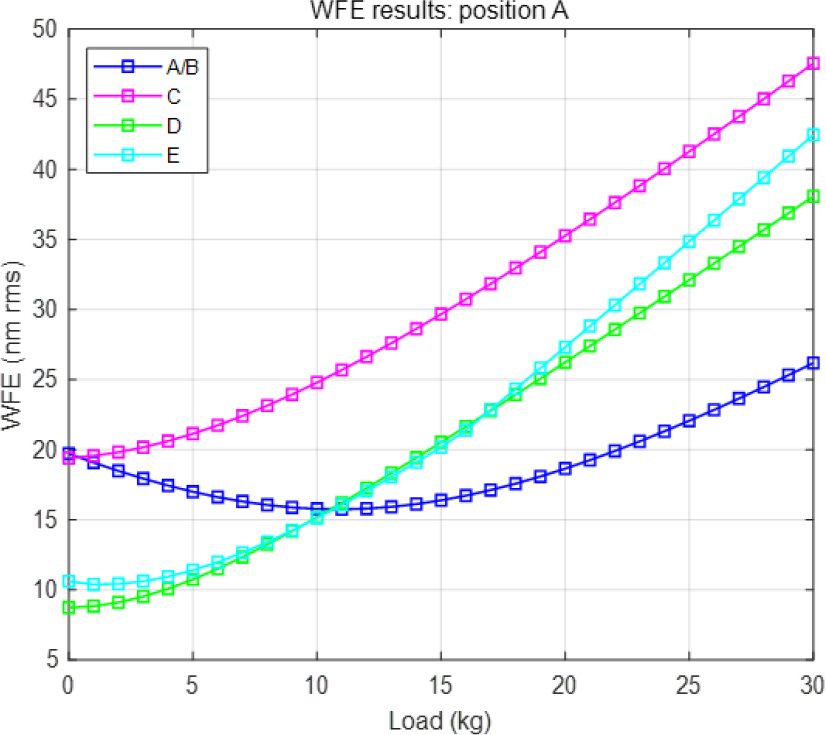
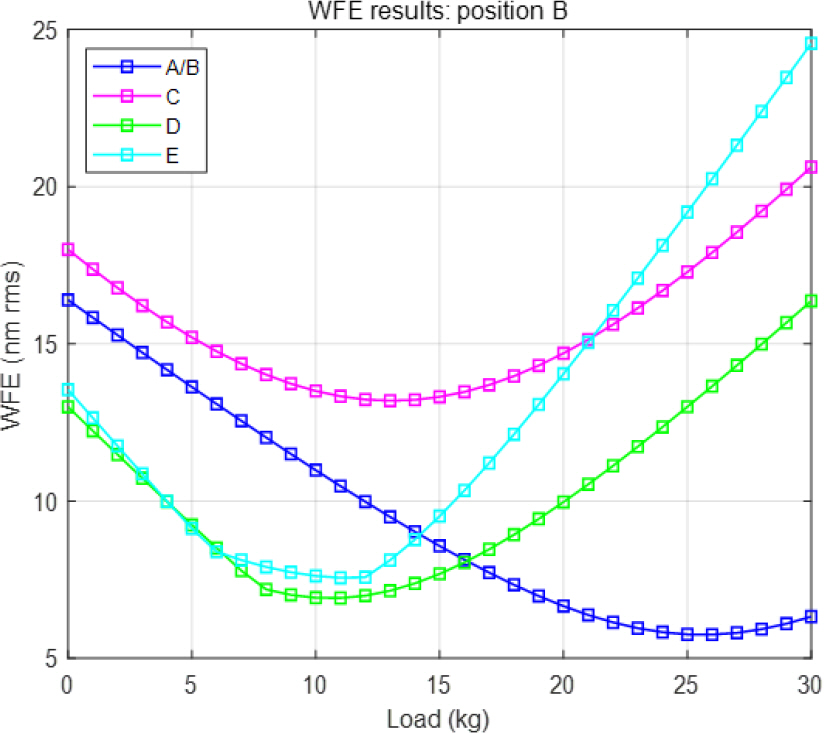
Global 좌표계로 산출된 질점의 이동량을 각 local 좌표계로 변환 후, 파면오차 발생량을 계산하였다. Fig. 23과 Fig. 24에 대역별 보상 하중에 따른 파면오차 발생량을 그래프화 하였다. X축은 보상 하중의 크기이며, 자중보상장치의 한쪽당 적용될 하중 크기를 기준으로 정리하였고 단위는 kg이다. Y축은 파면오차이며, 단위는 nm rms이다. 각 광학품의 민감도 때문에 보상 하중에 따른 파면오차 발생량은 대역별로 모두 다른 경향을 나타내는 것을 그래프를 통해 확인할 수 있다. Fig. 23을 통해 자중 보상 적용 위치가 A에 있을 경우, 분석한 보상 하중 범위에서 A/B 대역은 파면오차 버짓인 10 nm rms 이하를 모두 만족하지 못하는 것을 확인할 수 있다. 반면 Fig. 24를 통해 자중 보상 적용 위치가 B에 있을 경우, 5개의 대역 모두 파면오차 버짓을 만족하는 범위가 존재하는 것을 확인할 수 있다. 따라서 위치별 보상 하중에 따른 파면오차 결과를 통해 부 반사경 뒤인 B의 위치에 자중 보상을 적용하는 것으로 결정하였다.
자중 보상 적용 위치가 B에 있을 경우, A/B 대역은 보상 하중이 13 kg 이상일 때부터 파면오차 버짓인 10 nm rms 이하를 만족한다. C, D 대역은 분석한 보상 하중 범위에서 파면오차 버짓인 28 nm rms 이하와 20 nm rms 이하를 모두 만족하며, 각각 13 kg와 10 kg 의 보상 하중을 기준으로 경향이 바뀌는 것을 확인할 수 있다. E 대역의 경우 보상 하중 25 kg 이하에서 버짓 20 nm rms 이하를 만족하며, 10 kg의 보상 하중을 기준으로 경향이 바뀌게 된다. 따라서 본 연구에서 적용할 보상 하중의 크기는 모든 대역에서 할당된 파면오차 버짓을 만족하는 20 kg로 선정하였다. Table 9에 자중보상장치의 양쪽에 20 kg의 보상 하중을 각각 적용하였을 때와 자중 보상을 하지 않았을 때의 대역별 파면오차 발생량을 비교하였다. E 대역의 경우, 자중 보상을 하지 않았을 때보다 광학 성능이 다소 떨어지지만, 그 양이 1 nm rms 보다 작은 미소한 양으로 무시할 수 있다. 그 외 A/B, C, D 대역은 모두 광학 성능이 향상되었으며, 특히 가장 민감하고 버짓을 초과했던 A/B 대역에서 버짓을 만족하는 것을 확인할 수 있다.
결 론
본 논문에서는 5개의 파장 대역을 제공하는 위성용 EO/IR 탑재체인 다중대역광학센서 광구조체의 조립/정렬 시에 적용될 자중 보상 기법에 대해서 다루었다.
이를 위해 구조 건전성을 확보한 다중대역광학센서의 광구조체에 대하여 중력으로 인한 파면오차 발생량을 분석하였다. 구조해석을 통해 다중대역광학센서의 다층 구조물이 중력에 의해 변형되면서 발생한 광학 조립체의 무게 중심 이동량을 산출하고, 광학 민감도 정보와 함께 중력에 의한 파면오차를 계산하였다. 계산 결과, 가장 민감한 A/B 대역에서 할당된 파면오차 버짓을 충족시키지 못하는 것을 확인하였다. 따라서 중력으로 인해 발생하는 대역별 파면오차를 줄이기 위한 자중 보상 기법을 고안하였다.
본 연구에서 제안한 자중 보상 기법은 경통 앞단에 보상 하중을 가함으로써 광학적으로 가장 민감한 부 반사경의 위치를 중점적으로 조정함으로써 중력으로 인한 파면오차를 효율적으로 줄이는 방안이다. 이를 적용할 경우, 모든 대역에서 할당된 파면오차 버짓을 만족하는 것을 확인하였다. 향후 본 논문에서 제안한 자중 보상 기법이 적용된 자중보상장치를 제작하여 다중대역광학센서 광구조체의 조립/정렬 작업이 이루어질 계획이며, 해당 기법은 중력에 민감한 모든 위성용 광학 탑재체에서 활용될 수 있을 것으로 기대된다.