Prediction on the Performance of Polymer-Based Mechanical Low-Pass Filters for High-G Accelerometers

Sehwan Song; Junyong Jang; Youlim Lee; Hanseong Jo; Sang-Hee Yoon

doi:10.9766/KIMST.2023.26.3.262

Abstract

A polymer-based mechanical low-pass filter(m-LPF) for high-g accelerometers makes it possible to remove high-frequency transient noises from acceleration signals, thus ensuring repeatable and reliable measurement on high-g acceleration. We establish a prediction model for performance of m-LPF by combining a fundamental vibration model with the fractional derivative standard linear solid(FD SLS) model describing the storage modulus and loss modulus of polymers. Here, the FD SLS model is modified to consider the effect of m-LPF shape factor (i.e., thickness) on storage modulus and loss modulus. The prediction accuracy is verified by comparing the displacement transmissibility(or cut-off frequency) estimated using our model with that measured from 3 kinds of polymers(polysulfide rubber(PSR), silicone rubber(SR), and polydimethylsiloxane(PDMS)). Our findings will contribute a significant growth of m-LPF for high-g accelerometers.

Keywords: Prediction Model(예측 모델), Mechanical Low-Pass Filter(기계식 저역통과필터), Cut-Off Frequency(차단주파수), Polymer(고분자), Fractional Derivative Standard Linear Solid(분수도함수형 표준선형고체)

서 론

근래 고에너지 현상에 수반되는 가속도 측정에 관한 연구가 끊임없이 진행되고 있지만, 고충격 가속도 측정에 있어 반복도와 신뢰도의 향상은 여전히 난제로 남아있다. 이는 폭발, 금속-금속 충돌, 관통 등의 가속도는 20 kHz 수준의 신호가 상당히 존재하고 심지어 100 kHz 이상의 고주파수 잡음도 포함하기 때문이다. 일반적으로 고주파수 충격 에너지는 기계 장치에 구조적 손상을 거의 일으키지 않지만, 질량-스프링 형태의 가속도센서에 공진을 일으켜 물리적 구조, 측정 선형성 등의 측면에서 심각한 문제를 일으키게 된다. 지난 수십 년 동안의 급격한 기술 발전에도 불구하고 거의 모든 가속도센서의 작동원리는 고주파수 가진에 영향을 받음을 고려할 때 고충격 가속도 측정에 있어 가장 취약한 연결고리는 가속도센서 그 자체라 할 수 있다.

고충격 가속도 측정에는 압전형 가속도센서(piezoelectric accelerometer)와 압저항형 가속도센서(piezoresistive accelerometer)가 주로 사용된다. 두 종류의 가속도센서 모두 고충격 환경에서 물리적 파손(failure, 압저항형 가속도센서), 영점 변동(zero drift, 압전형 가속도센서) 및 비선형 출력 특성(non-linearity) 등의 문제점을 가지고 있는 것으로 알려져 있다^[1]. 지금까지 상기 문제점을 해결하기 위해 주된 접근 방법은 가속도센서의 고유진동수를 높이는 방식이었으나^[2], 이 방법은 가진(혹은 잡음)주파수가 센서의 고유진동수보다 높은 경우 효과가 없게 된다. 이에 가속도센서 감지부의 공기/기름 감쇠(air/oil damping)^[3], 감지부 변위 스토퍼(stopper)^[4], 저역통과필터(Low-Pass Filter, LPF) 등과 같은 방법도 연구되고 있다. 공기/기름 감쇠는 상대적으로 높은 수준의 기술과 복잡한 미세공정을 필요로 하고, 감지부 변위 스토퍼는 가속도센서의 측정범위를 제한하게 된다. 최근 가속도센서에 저역통과필터(Low-Pass Filter, LPF)를 적용하여 차단주파수(cut- off frequency) 이하의 신호만 통과시키는 방법이 주목받고 있다^[5]. 전기식 저역통과필터(electronic Low-Pass Filter, e-LPF)와 기계식 저역통과필터(mechanical Low- Pass Filter, m-LPF) 중에서 신호처리 분야에서 널리 사용되는 e-LPF는 센서의 출력단에 적용되어 가속도센서를 물리적으로 보호할 수 없는 반면 m-LPF는 센서로 입력되는 고주파수 가진을 미리 차단하기 때문에 가속도센서를 고주파수 가진으로부터 보호할 수 있다(Fig. 1). 따라서 m-LPF를 가속도센서에 적용할 경우, 고충격 측정의 반복도와 신뢰도를 효과적으로 향상시키게 된다. m-LPF의 소재로는 금속, 세라믹, 고분자 등이 있을 수 있는데, 금속은 감쇠 성능이 미흡하고 세라믹은 내고충격 및 감쇠 특성 측면에서 단점이 있다^[6]. 반면에 고분자는 진동 감쇠 특성이 매우 우수하고 성형이 용이하며 가속도센서의 온도 범위(-40 ℃ ∼ 70 ℃)도 만족시키기 때문에 m-LPF는 고분자로 구성하는 것이 바람직하다. 지금까지 고분자는 고충격 분야에서 주로 충격 절연기(shock isolator)로 사용되었고 가속도센서용 m-LPF로의 활용은 매우 제한적이다^[7]. 고분자는 물성(저장 탄성률(storage modulus), 손실 탄성률(loss modulus) 등)이 시간 혹은 주파수 의존성을 가지고^[8], 더불어 저장 탄성률과 손실 탄성률은 형상 인자(Shape Factor, SF)의 영향을 받기 때문에^[9,10] 고분자의 충격 응답 스펙트럼(shock response spectrum)은 예측하기 어려운 것으로 알려져 있다. 이에 현재는 다량의 실험을 통해 고분자의 충격 응답 스펙트럼을 확인하고 있다. 근래 들어 고분자의 고충격 환경 내 사용이 증가함에 따라 고분자의 충격 응답 스펙트럼을 예측할 수 있는 보편적 이론 및 방법에 대한 요구가 점점 증대되고 있다.

Fig. 1.

A comparison of mechanical low-pass filter(m-LPF) to electrical low-pass filter(e-LPF). An e-LPF (a) attenuating the output signals of an accelerometer above its cut-off frequency can't isolate the sensor from high-frequency transient noises, while a m-LPF (b) placed between structure surface and accelerometer removes high-frequency transient noises from acceleration signals.

본 논문에서는 고충격용 가속도센서에 적용가능한 고분자 기반 m-LPF의 성능(변위 전달률(displacement transmissibility) 혹은 차단주파수)을 예측할 수 있는 방법에 대해 기술한다. 먼저, 동적기계 분석기(Dynamic Mechanical Analysis, DMA)로 측정된 고분자의 저장 탄성률과 손실 탄성률을 분수도함수형 표준선형고체(Fractional Derivative Standard Linear Solid, FD SLS) 모델을 이용하여 주파수의 함수로 표현한다. m-LPF와 DMA 시편 형상(특히, 두께 차이)의 상이함 혹은 형상계수의 차이에 의한 저장 탄성률과 손실 탄성률의 변화는 상기 FD SLS 모델에 수직이동인자(vertical shift factor)를 도입하여 보완한다. 이때 수직이동인자와 형상계수의 관계는 두께가 상이한 고분자 판재에서 측정한 변위 전달률로부터 얻는다. 최종적으로 변위 전달률에 관한 진동 이론에 수직이동인자를 반영한 FD SLS을 적용함으로써 고분자 기반 m-LPF의 성능을 예측하는 모델을 개발한다. 마지막으로 다황화물계 고무(Polysulfide Rubber, PSR), 실리콘 고무(Silicone Rubber, SR)와 폴리디메틸실론산(Polydimethysiloxane, PDMS)으로 구성된 m-LPF에 대해 차단주파수를 측정하고 그 결과를 본 연구에서 개발된 모델의 예측값과 비교함으로써 개발한 모델의 예측 정확도를 확인한다.

이론

2.1 변위 전달률

기저(base) 위에 놓인 질량 m, 댐퍼 c 및 스프링 k로 구성된 1자유도 진동계에서 상기 기저가 가진되는 경우에 운동방정식은 mx¨+c(x˙−y˙)+k(x−y)=0이다. 여기서 x(t)와 y(t)는 각각 질량과 기저의 변위이다(Fig. 2a). 기저가 y(t) = Y₀e^iωt로 조화진동을 하면 진동계의 변위는 x(t) = X₀e^{i(ωt - ϕ)} 의 형태를 가지고 상 기 1자유도 진동계의 변위 전달률 T₀는 다음과 같이 표현된다.

Fig. 2.

1-DOF system subjected to harmonic base excitation. (a) Damped spring (or Kelvin-Voigt) model. (b) Viscoelastic model. (c) Physical representation of viscoelastic models including GM model, SLS model, and FD SLS model. The dynamic stiffness of each model is also summarized. (d) Spring-pot element of the FD SLS model, compared with spring and damper.

(1)

T0=|X0Y0|=k2+(cω)2(k−cω2)2+(cω)2

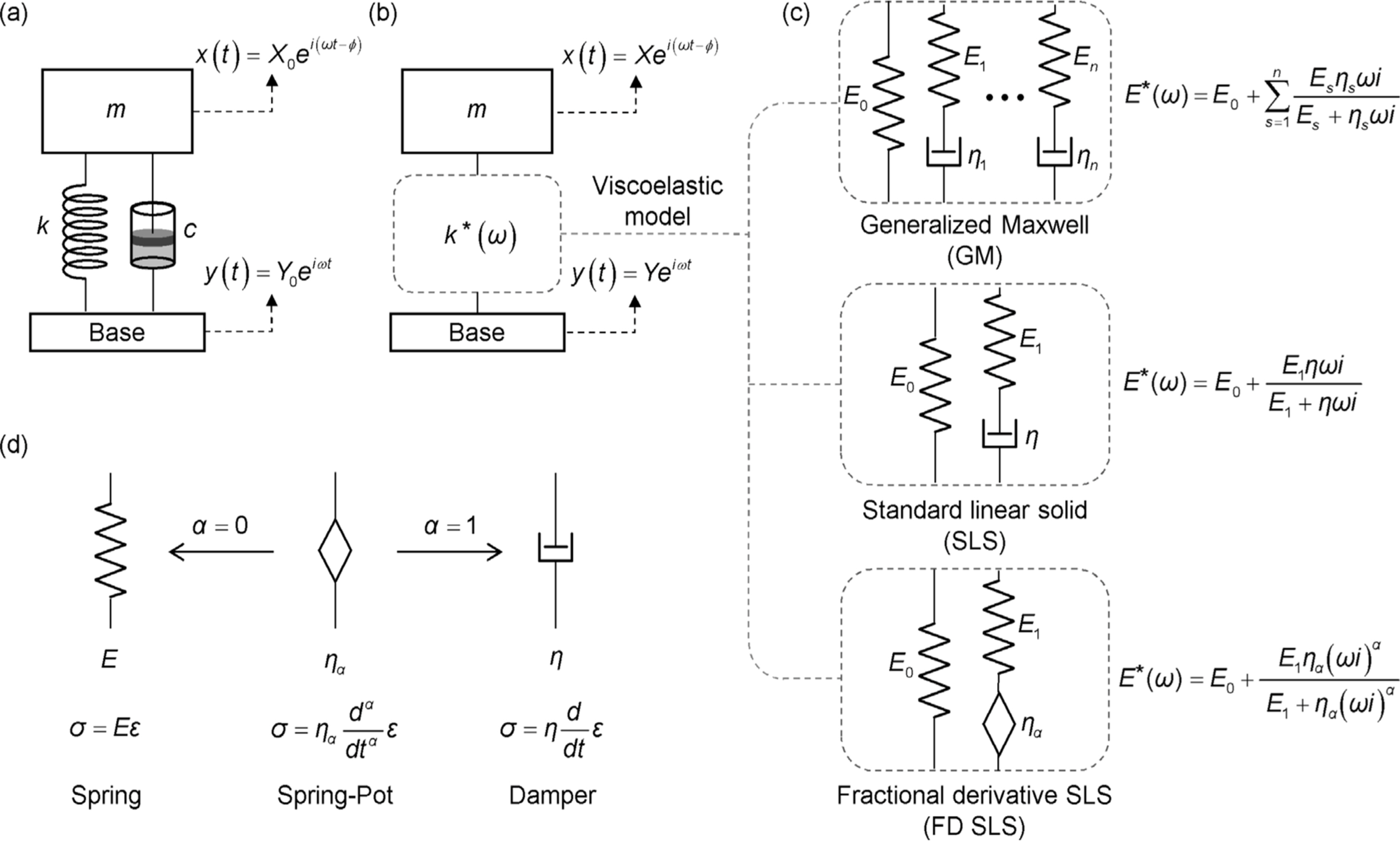
고분자는 물성이 가진주파수의 영향을 받기 때문에 고분자로 구성된 1자유도 진동계(Fig. 2b)의 변위 전달률 T는 저장 탄성률을 상수(constant)로 가정하는 식 (1)으로 충분히 예측할 수 없다. 일반적으로 고분자의 물성은 동적 계수(dynamic modulus) E^*(ω) = E′(ω)+iE”(ω)를 이용하여 표현한다. 여기서, E^*의 실수부인 E′ ′는 저장 탄성률이고 허수부인 E” ″는 손실 탄성률이 다. 고분자의 E^*는 Maxwell 모델, Kelvin-Voigt 모델, Generalized Maxwell(GM) 모델, 표준선형고체(Standard Linear Solid, SLS) 모델, FD SLS 모델 등의 다양한 점탄성 모델을 이용하여 나타낸다(Fig. 2c)^[11]. 참고로, n = 1인 GM 모델은 SLS 모델에 해당하고, 상기 SLS 모델에서 댐퍼 c를 spring-pot으로 대체한 것이 FD SLS 모델이다(Fig. 2d). 지름이 d이고 두께가 h인 원통 형상 의 고분자에 있어 동적 계수 E^*와 동적 강성(dynamic stiffness) k^*사이의 관계는 k^*(ω) = k′(ω)+ik”(ω)=E^*(ω)d²π/(4h)이다. 상기 원통 형상의 고분자를 FD SLS 모델로 나타낼 경우, 상기 고분자로 구성된 1자유도 진동계의 T는 다음과 같이 표현할 수 있다(Fig. 2b 참조).

(2)

T=E′2+E′′2(E′−4hmω2/(d2π))2+E′′2

여기서 E′ ′과 E”″는 FD SLS의 동적 계수에 의해 각각

E0E12+(2E0E1+E12)ηαωαcos⁡(απ/2)+(E0+E1)(ηαωα)2E12+2E1ηαωαcos⁡(απ/2)+(ηαωα)2

와E12ηαωαsin⁡(απ/2)E12+2E1ηαωαcos⁡(απ/2)+(ηαωα)2 로 나타낼 수 있다.

2.2 형상계수

일반적으로 재료의 물성은 형상의 영향을 받지 않으나, 고분자는 두께가 얇은 경우 E′과 E′′등의 물성은 형상의 영향을 받는 것으로 알려져 있다. 재료의 형상이 물성에 미치는 영향은 형상계수 SF를 이용하여 표현하게 된다. 지름이 d이고 두께가 h인 원통형 m-LPF의 경우, SF = Loaded area / Force-free area = d/(4h)이다. SF가 E′과 E′′에 미치는 영향을 표현하기 위해 SF < SF^*인 경우 E′의 수직이동인자 β_E′와 E′′의 수직이동인자 β_E”는 1이고, SF ≥ SF^*인 경우 β_E′과 β_E”은 SF와 선형적이라고 가정하면 두 수직이동인자와 SF의 관계는 다음과 같이 표현된다. 참고로, SF^*는 β_E′ = 1 과 β_E” = 1 을 만족하는 SF 값이다.

(3)

βE′(SF)=1(SF<SF∗)=s(SF−SF∗)+1(SF≥SF∗)

(4)

βE′′(SF)=1(SF<SF∗)=l(SF−SF∗)+1(SF≥SF∗)

여기서 s와 l은 각각 βE_′과 βE_″의 수직이동인자를 나타내기 위한 상수이다. 상기 수직이동인자를 반영한 E′과 E″는 다음과 같이 정리할 수 있다.

(5)

E′(ω,SF)=βE′(SF)×E0′(ω),E′′(ω,SF)=βE′′(SF)×E0′′(ω),

여기서 E0′(ω)과 E0′′(ω)는 각각 DMA를 통해 측정 된 SF < SF^*를 만족하는 고분자 시편의 저장 탄성률과 손실 탄성률이다. 따라서 FD SLS 모델로 표현된 고분자로 구성된 1자유도 진동계의 T를 수직이동인자(혹은 형상계수)를 반영한 E′과 E″로 나타내면 식 (2)로부터 다음과 같이 정리할 수 있다.

(6)

T=E0′2+E0′′2(E0′−4hmω2/(d2π))2+E0′′2(SF<SF∗),=(s(SF−SF∗)+1)2E0′2+(l(SF−SF∗)+1)2E0′′2[(s(SF−SF∗)+1)E0′−4hmω2/(d2π)]2+(l(SF−SF∗)+1)2E0′′2(SF≥SF∗).

재료 및 방법

3.1 재료

PSR의 재료인 코레실 PS9210(L)(유리전이온도: - 55 ℃, 분자량: 367.4 g/mol)은 KCC사에서 제공받았고, SR의 재료인 Dragon Skin ^TM 10 NV(유리전이온도: - 125 ℃, 분자량: ∼650,000 g/mol)는 Smooth-On사에서 구매하였으며, PDMS의 재료인 Sylgard 184(유리전이온도: - 123 ℃, 분자량: ∼74.2 g/mol)는 Dow Corning사에서 구입하였다. 모든 재료는 추가적인 처리나 가공없이 제공된 형태로 사용되었다.

3.2 m-LPF 제작

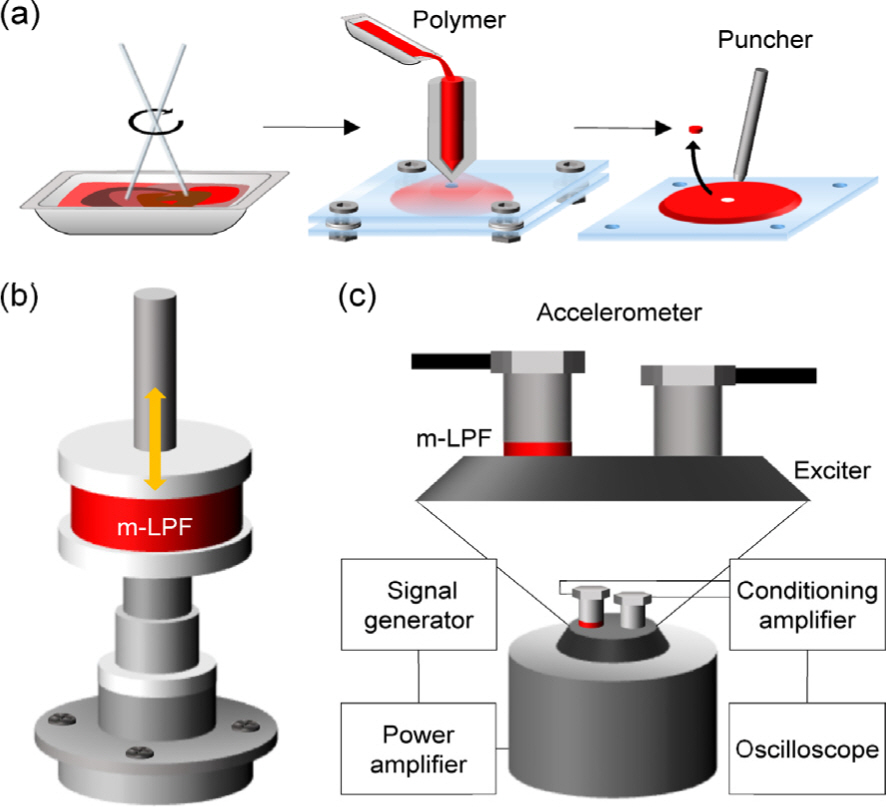
m-LPF는 3종의 고분자를 사출성형 및 펀칭(punching)하여 제작하였다(Fig. 3a). 각 고분자의 주제와 경화제를 혼합한 후 내부의 기포를 충분히 제거하였다. 코레실 PS9210(L), Dragon Skin ^TM 10 NV 및 Sylgard 184에 있어 주제와 경화제의 혼합중량비는 각각 1.0:0.8, 1.0:1.0 및 1.0:0.1이었고, 혼합시간은 공통적으로 10분이었다. 잘 혼합된 3종의 고분자는 2 kPa에서 60분동안 탈포하였다. 준비된 각각의 고분자를 아크릴 소재의 주형에 주입한 후, 70 ℃ 조건에서 충분히 경화시켰다. PSR, SR 및 PDMS의 경화시간은 각각 24시간, 2시간 및 6시간이었다. 마지막으로 경화가 완료된 고분자 판재를 펀칭하여 m-LPF를 준비하였다.

Fig. 3.

Experimentals. (a) Manufacturing processes composed of blending each base with its curing agent for 10 m (left), injecting the polymer solution into a mold, and drying at 70 ℃ (center), followed by die punching of the polymer film (right). (b-c) Experimental set-up for DMA measurement under compression (b) and vibration test using exciter (c).

3.3 동적기계 분석

3종 고분자의 물성은 동적기계 분석기(TA Instruments, DMA850)로 측정하였다(Fig. 3b). DMA용 시료는 두께가 5.0 mm이고 지름이 12.5 mm이었다. 각각의 시료에 크기는 5 % 이고 주파수는 1-80 Hz인 사인파형의 변형률을 가해주면서 저장 탄성률과 손실 탄성률을 측정하였다. 측정은 - 40 ℃에서 20 ℃까지 20 ℃ 간격으로 이루어졌고 각 온도별로 측정 시간은 30분이었다. 동적기계 분석을 통해 측정된 고분자의 물성은 시간-온도 중첩원리(Time-Temperature Superposition principle, TTS 원리)를 적용하여 저장 탄성률과 손실 탄성률의 마스터 곡선(master curve)을 획득하였다^[12]. 마스터 곡선을 획득할 때 필요한 수평이동인자(horizontal shift factor)는 Williams-Landel-Ferry(WLF) 방정식을 통해 결정하였다^[13].

3.4 진동 실험

m-LPF 위에 설치된 가속도센서(실험군, Brüel & Kjær type 4516)와 m-LPF 없이 설치된 동일한 가속도센서(대조군)를 0.01-20 kHz, 50 g(약 490 m/s²)로 가진하며 각 가속도센서의 출력신호를 측정하였다(Fig. 3c). 상기 가진 환경은 파형 발생기(Keysight 33500B), 전력 증폭기(Brüel & Kjær type 2706) 및 가진기(Brüel & Kjær type 4809)를 이용하여 구현하였다. 상기 가속도센서의 출력신호는 신호처리 증폭기(Brüel & Kjær type 1704-A-002)와 오실로스코프(Keysight EDUX1052G)를 이용하여 측정하였다.

결과 및 논의

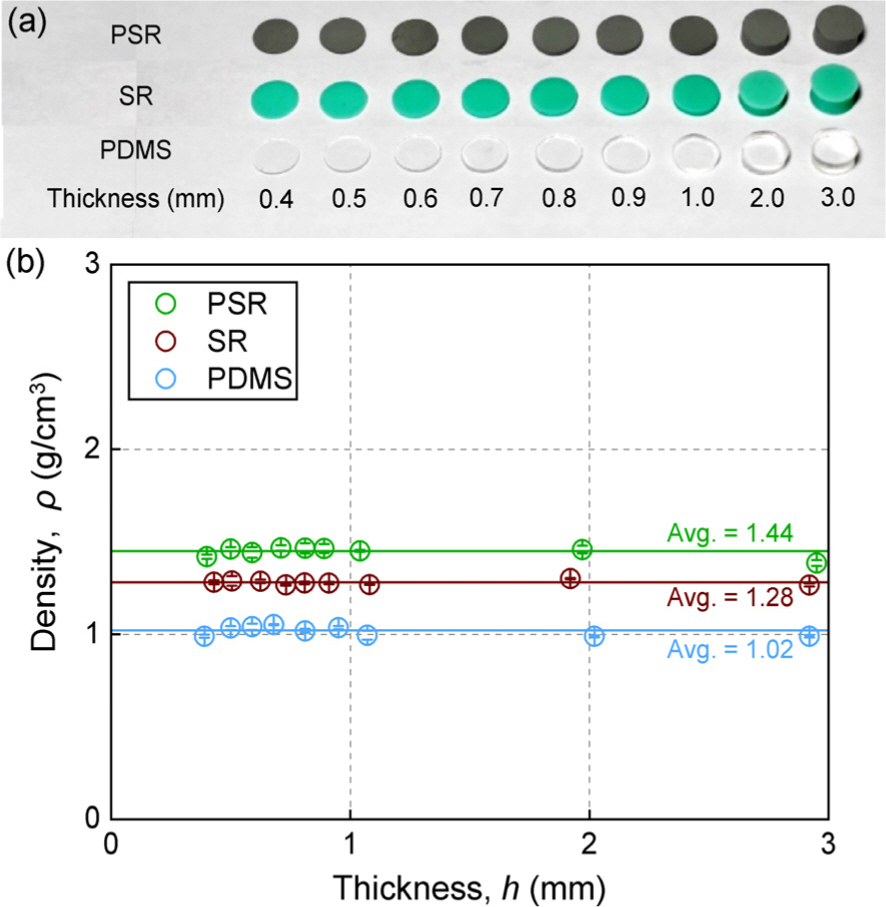
고분자 기반 m-LPF의 변위 전달률(혹은 차단주파수)를 예측하는 모델의 정확도를 확인하기 위해 PSR, SR 및 PDMS로 m-LPF를 제작하였다. 고분자 m-LPF의 두께는 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 2.0 및 3.0 mm이었다(Fig. 4a). 고분자로 m-LPF 제작 시 내부에 형성되는 공극은 그 성능에 영향을 미치기 때문에 m-LPF의 제작 수준을 확인하는 인자로 밀도를 측정하였다. PSR, SR 및 PDMS로 제작된 m-LPF의 평균 밀도는 각각 1.44, 1.28 및 1.02 g/cm³이었고 각 고분자 제조사의 기술자료에 명시된 값(1.44, 1.25 및 1.03 g/cm³)과 최대 2.40 % 의 차이를 보였다(Fig. 4b). 더불어 제작 두께에 따른 밀도의 차이는 최대 4.03 % (PDMS 시료)이었다.

Fig. 4.

Physical characterization of m-LPFs. (a) Optical images of a set of m-LPFs made of PSR, SR, and PDMS having different thicknesses of 0.4, 0.5, 0.6, 0.7, 0.8, 0.9, 1.0, 2.0, and 3.0 mm. (b) Density vs. thickness for m-LPFs made of PSR, SR, and PDMS.

4.1 저장 탄성률과 손실 탄성률

3종 고분자의 동적 물성(저장 탄성률과 손실 탄성률)은 형상계수 0.625를 가지는 시편을 이용하여 DMA로 측정하였다. 각 고분자 시편의 저장 탄성률과 손실 탄성률에 대한 마스터 곡선은 - 40 ºC, - 20 ºC, 0 ºC와 20 ºC에서 1-80 Hz에서 측정된 저장 탄성률과 손실 탄성률에 대해 TTS 원리를 적용하여 획득하였다. 상세하게는 각각의 온도에서 측정된 저장 탄성률과 손실 탄성률의 기준 온도(20 ºC) 저장 탄성률과 손실 탄성률에 대한 수평이동인자는 TA Instruments의 TRIOS 프로그램을 통해 구하였고, 관련 실증적 모델 중 가장 대표적인 WLF 방정식을 이용하여 각각의 마스터 곡선을 얻었다. PSR을 포함한 모든 고분자는 특정 온도 조건에서 주파수가 증가함에 따라 그 저장 탄성률과 손실 탄성률이 증가하였고 특정 주파수 범위 조건에서 온도가 감소함에 따라 동적 물성은 증가하였다(Fig. 5). 이는 널리 알려진 고분자 동적 물성의 시간 의존 특성^[14] 및 온도 의존 특성^[15]과 일치한다. 더불어 점탄성 거동 특성을 가진 고분자의 낮은 온도에서 측정된 동적 물성은 동일 온도의 높은 주파수의 동적 물성에 해당하고 높은 온도에서 측정한 동적 물성은 낮은 주파수에서의 동적 물성에 해당된다는 TTS 원리에도 부합한다. 다음으로, PSR의 마스터 곡선은 주파수가 증가함에 따라 그 저장 탄성률은 0.31 MPa에서 3.54 MPa로 증가하고 손실 탄성률도 0.08 MPa에서 3.92 MPa로 증가함을 보여준다. 일반적으로 주파수가 증가함에 따라 고분자의 저장 탄성률은 증가 후 수렴하고 손실 탄성률은 증가 후 감소하는 비단조 거동을 보임^[16]을 고려할 때, PSR은 1-20,000 Hz에서 유리 전이(glass transition) 상태에 있는 것으로 판단된다^[17].

Fig. 5.

DMA measurement on PSR, resulting in its master curves of storage modulus and loss modulus at a reference temperature of 20 ℃. (a) Comparison of viscoelastic models for describing storage modulus vs. frequency (b) Comparison of viscoelastic models for expressing loss modulus vs. frequency.

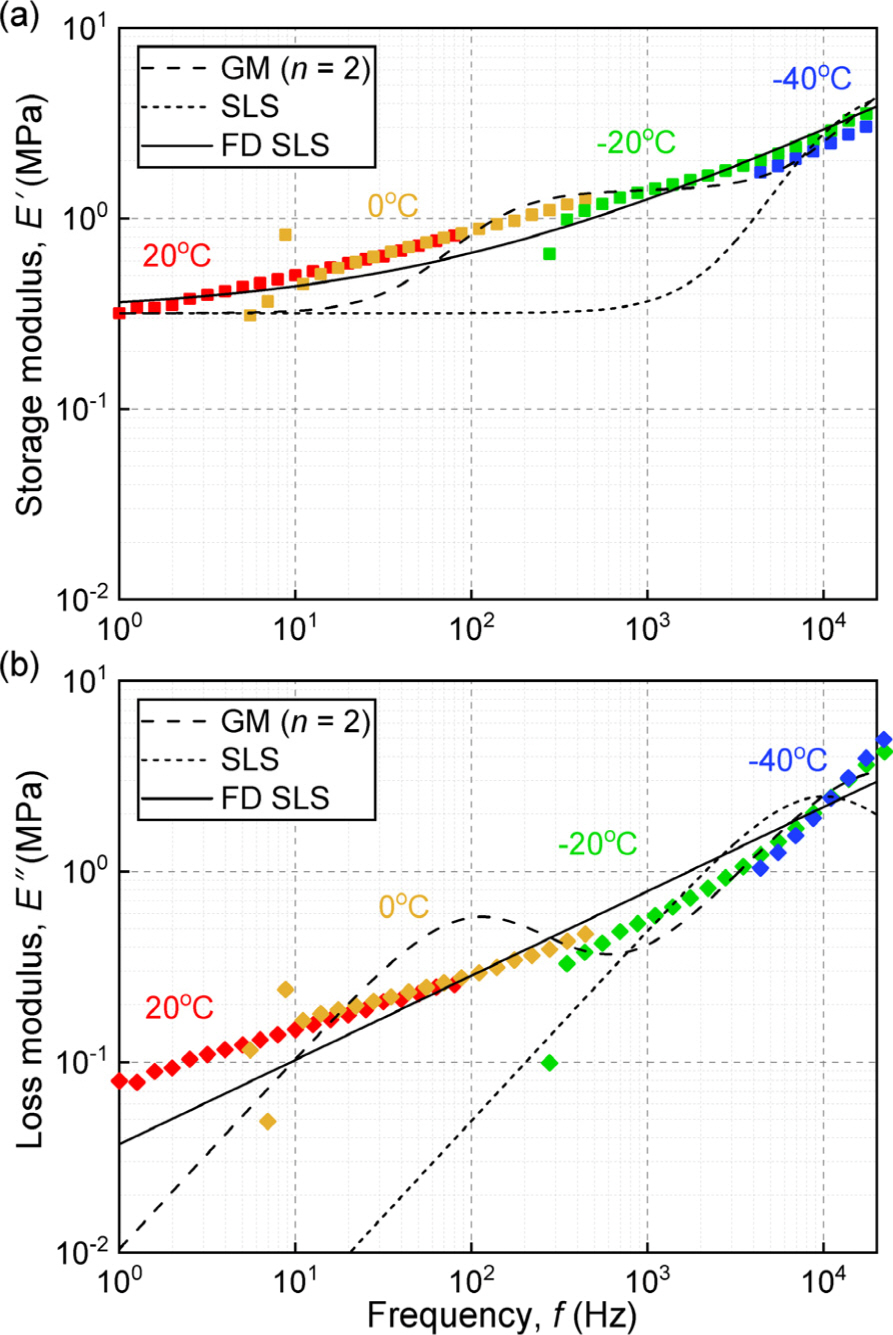
고분자 기반 m-LPF의 성능 예측의 첫번째 단계는 각 고분자의 저장 탄성률과 손실 탄성률을 주파수의 함수로 표현하는 것이다. 본 연구에서는 다양한 점탄성 모델 중 크리프(creep)와 응력 완화(stress relaxation)를 표현할 수 있는 GM 모델(n = 2), SLS 모델 및 FD SLS 모델을 고려하였다. 상기 모델들을 앞서 측정한 3종 고분자의 저장 탄성률과 손실 탄성률에 대한 마스터 곡선 데이터에 적용한 결과, FD SLS 모델의 결정계수(coefficient of determination, r²)는 0.96으로 고분자의 저장 탄성률과 손실 탄성률을 주파수의 함수로 나타내는데 가장 적합하였다(Fig. 5 참조). 최소자승법 기반 비선형회귀법을 통해 결정된 3종의 고분자에 대한 FD SLS 모델의 계수 값은 Table 1과 같다. 이 결과는 추후 고분자 기반 m-LPF의 성능 예측 모델의 개발에 활용된다.

Table 1.

Parameter values of the FD SLS model used in describing the storage modulus and loss modulus of polymers

Polymer	Parameter in FD SLS
Polymer	E₀ (Pa)	E₁ (Pa)	η_α (Pa·sec^α)	α
PSR	3.18×10⁵	2.55×10¹⁰	2.56×10⁴	4.42×10^-1
SR	3.37×10⁶	4.18×10⁷	3.97×10⁴	3.24×10^-1
PDMS	3.31×10⁶	4.24×10⁷	2.82×10⁵	3.30×10^-1

4.2 m-LPF 성능 예측 모델

3종의 고분자(PSR, SR 및 PDMS) 기반 m-LPF의 전달률을 측정함으로써 고분자의 저장 탄성률과 손실 탄성률에 대한 시편 형상계수의 효과를 정량화하였다. 지름이 6.3 mm이고 두께가 0.4, 1.0 및 3.0 mm로 형상계수가 3.938, 1.514 및 0.534인 고분자 시편이 실험군이었고, 동일 고분자로 만들어진 형상계수가 0.625인 DMA 분석용 시편이 대조군이었다. 진동 실험을 통해 측정한 각 실험군의 변위 전달률을 식 (6)으로 최소자승법 기반 비선형 회귀 분석을 수행함으로써 각 고분자에 있어서 수직이동인자(β_E′, β_E″)와 형상계수의 관계를 확인하였다. 기존 연구와 마찬가지로 3종 고분자의 저장 탄성률과 손실 탄성률은 시편의 형상계수가 1보다 작은 경우에는 형상계수와 상관없이 동일한 값을 가졌지만, 형상계수가 1보다 큰 경우에는 형상계수에 비례하여 급격히 증가하였다(Fig. 6). 본 연구에서는 고분자의 동적 물성이 형상계수에 의해 영향을 받지 않는 영역(SF < SF)에서는 β_E′과 β_E″를 1로 취급하였고, 형상계수에 의해 영향을 받는 영역(SF ≥ SF)에서는 두 수직이동인자와 형상계수는 선형 관계를 가지는 것으로 표현하였다(식 (3), 식 (4) 참조). 선형회귀법을 통해 결정된 3종 고분자의 수직이동인자는 Table 2와 같다. 이를 통해 고분자를 FD SLS 표현하고 상기 고분자 시편의 형상계수에 의한 그 동적물성 변화를 정량화함으로써 고분자 기반 m-LPF의 성능을 예측할 수 있는 모델을 개발하였다.

Fig. 6.

Vertical shift factors (β_E’ and β_E”) vs. shape factor for m-LPF. (a) Displacement transmissibility of PSR m-LPFs having different thicknesses (or SFs). (b-c) Storage modulus (b) and loss modulus (c) obtained from the least-square regression analysis, compared with their master curves obtained from the sample having a SF of 0.625. (d) Vertical shift factor as a function of shape factor for PSR (left), SR (center), and PDMS (right).

Table 2.

Vertical shift factors of storage and loss moduli for PSR, SR, and PDMS

Polymer	Vertical shift factor
Polymer	S	l	SF^*
PSR	8.238	9.761	0.938
SR	6.463	17.479	0.688
PDMS	3.033	5.411	0.657

4.3 예측 모델의 검증

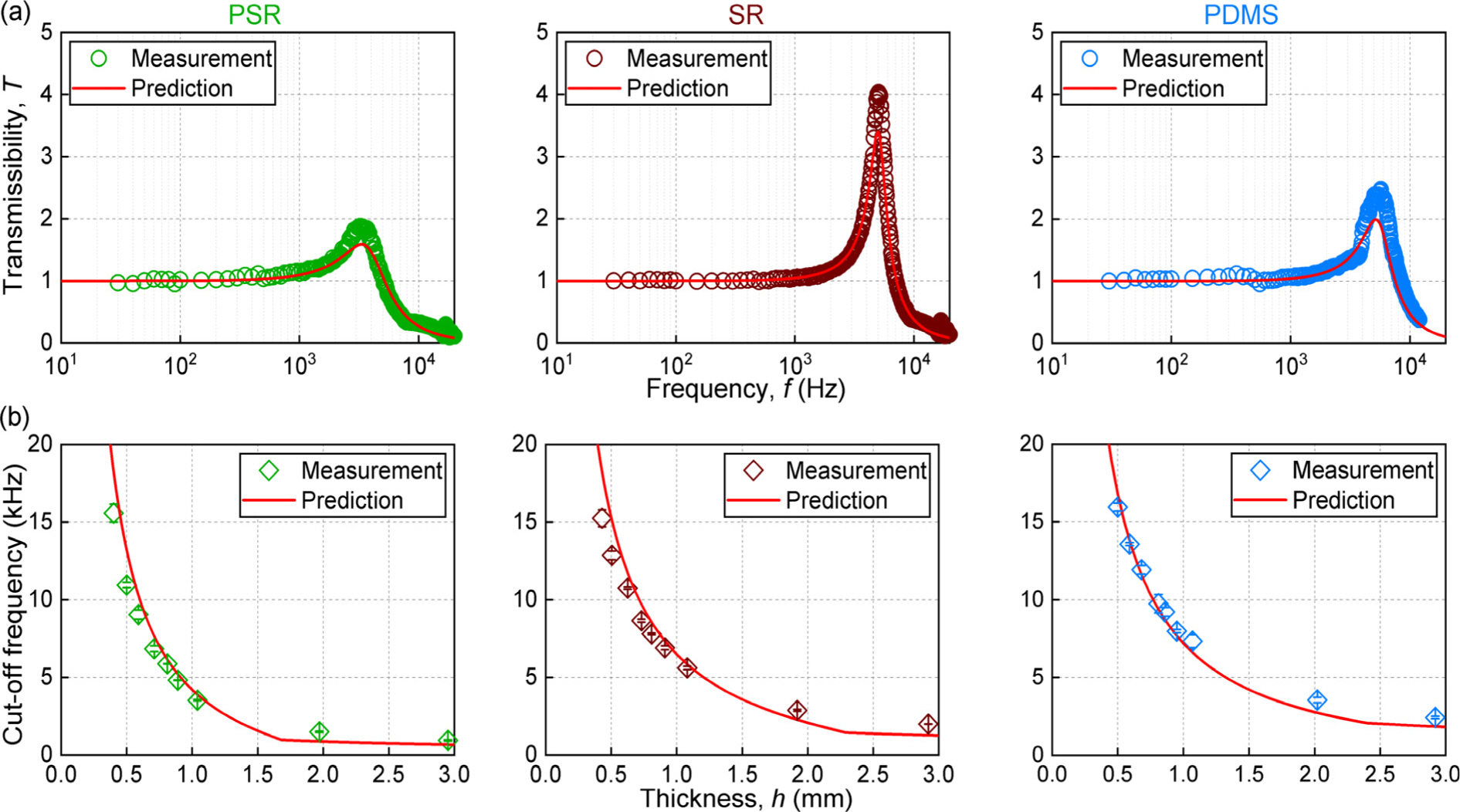
본 연구를 통해 개발한 m-LPF 성능 예측 모델의 정확도는 2가지 방법으로 확인하였다. 첫번째 방법은 3종 고분자로 제작되고 지름이 6.4 mm이며 두께가 0.5, 0.6, 0.7, 0.8, 0.9 및 2.0 mm인 시편(모델 개발에 사용되지 않은 시편)에 대해 진동 실험을 통해 측정한 차단주파수 혹은 변위 전달률을 예측 모델을 통해 계산된 값과 비교하는 것이었다. 먼저, 3종 고분자로 구성된일정 두께를 가지는 m-LPF의 변위 전달률을 측정 및 예측하여 비교하였고 그 결과를 바탕으로 차단주파수 측정치와 예측치를 확인하였다. Fig. 7a는 0.8 mm 두께를 가지는 m-LPF의 변위 전달률에 대한 측정치와 예측치를 보여주고 있다. 변위 전달률에서 확인할 수 있는 다양한 지표(차단주파수, 최대 전달률 및 공진주파수) 측면에서 측정치와 예측치가 매우 유사한 것을 확인하였다. 더불어 3종 고분자로 구성된 두께가 다른 m-LPF의 차단주파수 측정치와 예측치를 비교한 결과, 평균오차가 14.2(PSR), 12.4(SR) 및 7.9 % (PDMS) 수준이었다(Fig. 7b). 3종 고분자 시료 제작 시 형성된 내부 공극으로 인한 차단주파수의 변화를 고려할 때, 본 연구의 개발 모델은 고분자 기반 m-LPF 의 저역통과성능을 충분히 예측할 수 있을 것으로 판단된다. 더불어 고충격 가속도센서용 고분자 기반 m-LPF의 성능은 고분자의 선정뿐만 아니라 그 형상(특히, 두께)을 조절하는 방식으로도 조절할 수 있음을 확인할 수 있었다.

Fig. 7.

Prediction accuracy. (a) A comparison between predicted displacement transmissibility and measured one for 0.8 mm-thick m-LPFs made of PSR (left), SR (center), and PDMS (right). (b) Cut-off frequency vs. thickness measured from m-LPFs made of PSR (left), SR (center), and PDMS (right).

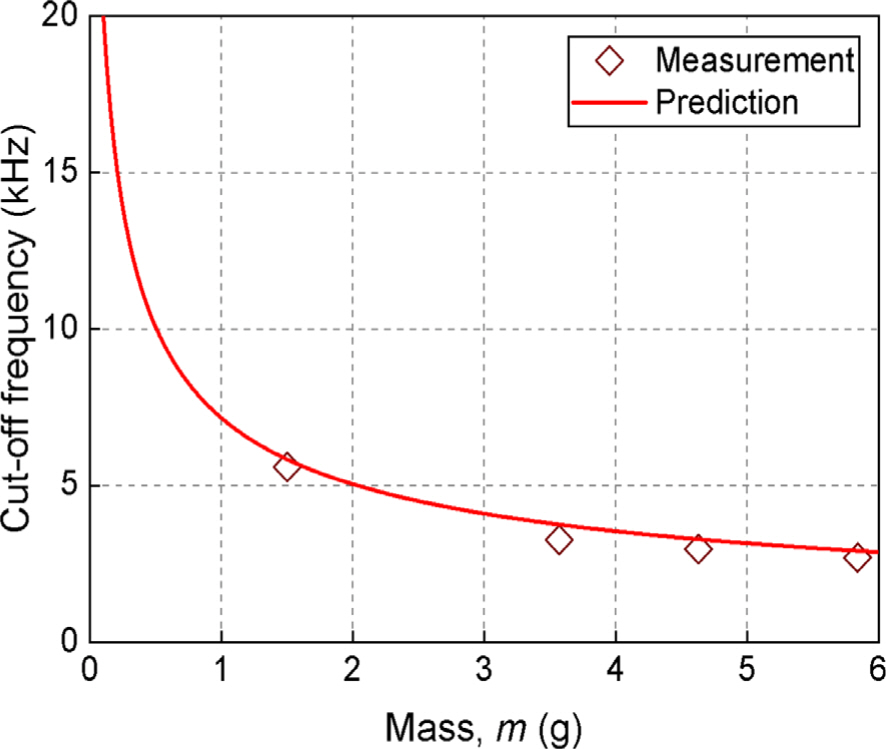
두번째 방법은 m-LPF 위에 놓이는 질량을 변화시키면서 측정한 차단주파수와 개발된 모델을 통해 예측된 차단주파수를 비교하는 것이다(Fig. 8). 본 연구에서는 SR로 제작되고 지름 6.3 mm, 두께 1.0 mm인 m-LPF 상부 면에 1.50, 3.57, 4.63 및 5.84 g의 질량(m-LPF의 질량포함)을 가해주면서 상기 질량의 변위 전달률을 측정하고 이로부터 차단주파수를 획득한 후 이를 우리 모델의 예측치와 비교하였다. 그 결과 차단주파수를 예측함에 있어 최대 오차가 13.0 % 이내임을 확인하였다. 상기 결과 역시 본 연구를 통해 도출된 고분자 기반 m-LPF의 성능에 대한 예측 모델의 우수성을 보여주고 있다.

Fig. 8.

Evolution in the cut-off frequency of 1.0 mm -thick SR m-LPF caused by a variation of mass (including m-LPF mass) of 1-DOF system, compared with cut-off frequency calculated with our prediction model.

결 론

본 연구에서는 고충격 가속도센서의 측정 반복도와 신뢰도를 향상시키기 위한 고분자 기반 m-LPF의 성능을 예측할 수 있는 기술을 개발하였다. 상기 예측 모델은 3단계를 거쳐 개발하였다. 먼저 고분자의 동적 물성인 저장 탄성률과 손실 탄성률을 DMA로 측정한 후 이를 점탄성 모델을 이용하여 주파수의 함수로 표현하였다. 다양한 점탄성 모델 중 FD SLS 모델이 고분자의 동적 물성을 최적으로 표현하는 모델임을 확인하였다. 다음으로 형상계수가 상이한 원판형 고분자 m-LPF의 변위 전달률을 측정하여 형상계수에 의한 고분자 동적 물성의 변화를 정량화한 후 이를 수직이동인자를 도입하여 보완하였다. 마지막으로 기존 진동이론에 수직이동인자를 반영한 FD SLS 모델을 적용함으로써 고분자 기반 m-LPF의 성능 예측 모델을 개발하였다. 본 연구를 통해 개발한 모델의 예측 정확도를 확인하기 위해 다양한 두께를 가지는 m-LPF의 변위 전달률(혹은 차단주파수) 측정값과 그 예측값을 비교하였다. 더불어 고분자 기반 m-LPF를 포함하는 1자유도 진동계의 질량 변화에 따른 차단주파수 변화에 대한 측정값과 예측값도 비교하였다. 이를 통해 상기 모델은 고분자 기반 m-LPF의 저역통과성능을 오차범위 11.5 % 이내로 충분히 예측할 수 있음을 확인하였다. 본 연구 결과는 고충격 가속도센서용 m-LPF의 설계에 널리 활용되어 궁극적으로 고충격 가속도센서의 측정 정확도를 높이는데 기여할 것으로 기대된다.