Article information

Trans Abstract

1. 서 론

레이저를 원거리 표적에 정밀 집속시킬 목적으로 레이저 무기의 광집속기에는 다수의 광학미러가 장착된다. 광학미러에는 열-기계적 하중에 의한 수십 나노미터(nm)의 변형만으로도 고에너지 집속 성능이 저하되는 문제가 발생한다. 광학미러 조립체의 구성품 간의 재료물성치 차이로 인하여 온도 변화와 자중에 의해서 광학미러의 표면이 변형되는데, 이 변위를 Zernike 다항식으로 근사하여서, 파면오차라는 광학시스템의 성능지수로 규정한다. 광학미러를 지지하는 마운트에 유연힌지(Flexure Hinge) 구조를 적용함으로써, 광학미러의 변형을 억제함으로써 궁극적으로 파면오차를 최소화하는 연구가 진행되어 왔다. 또한, 광학미러를 고속으로 정밀 구동하기 위해서, 광학시스템에 일정 수준 이상의 강성이 요구된다. 따라서, 고에너지 레이저 무기 개발에 있어서, 반경 방향 자유도에 대해서는 유연하고, 나머지 자유도에 대해서는 일정 수준 이상의 강성을 갖는 유연힌지 구조의 설계가 중요하다. 통상, 광학미러 마운트에는 소형∙경량화 및 고강성을 구현하기 위해서 열팽창이 적고 강성이 큰 소재를 사용하여 유연힌지가 구현되는데, 형상이 복잡할수록 제작에 많은 비용이 소요되므로, 최대한 단순한 구조로 설계될 필요가 있다.

열적∙기계적 변형에 의한 광학미러의 파면오차 분석과 실험계획법을 이용한 유연힌지 마운트의 최적설계에 관해 많은 연구가 있어왔다. Kim 등은 반사경 측면에 부착된 유연힌지의 치수를 반응표면법을 이용하여 최적화하였다^[1]. 그 밖에, 반사경의 강성 극대화를 위한 반사경 후면 지지구조 및 파면오차를 줄이기 위한 유연힌지의 설계에 관한 연구^[2,3], 광학미러 조립체에 대한 파면오차 해석을 통한 광학미러와 마운트의 최적 체결력 도출 연구^[4], 위상최적화를 이용한 광학미러 마운트의 경량화 연구^[5] 등이 소개되었으며, 특정 부위의 열변형을 억제하는 컴플라이언스 메커니즘(Compliance Mechanism) 설계에 관한 위상최적화 연구도 소개되었다^[6].

또한, 광학미러와 유연힌지 마운트 연결부의 열응력을 제한조건으로 고려하여 위상최적화 기법으로 유연힌지의 형상을 설계하는 방법이 최근에 제안되었다^[7].

본 논문에서는 반응표면법을 이용하여, 저차의 고유진동수를 1 kHz 수준 이상이면서 광학미러의 파면오차가 최소화된, 직경 100 mm급의 소형 광학미러용 유연힌지 일체형 마운트의 최적설계 연구 결과를 소개한다.

2. 연구 대상 및 목적

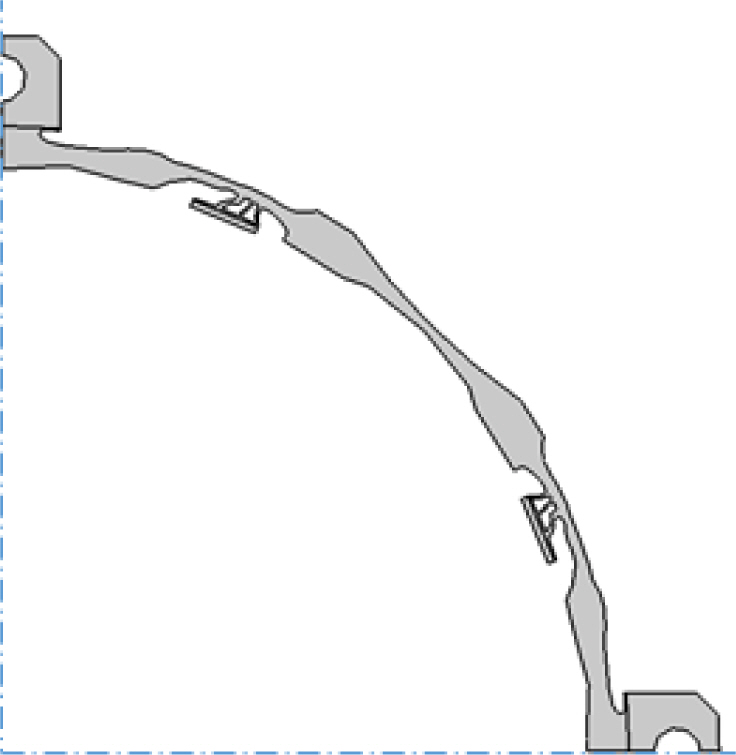
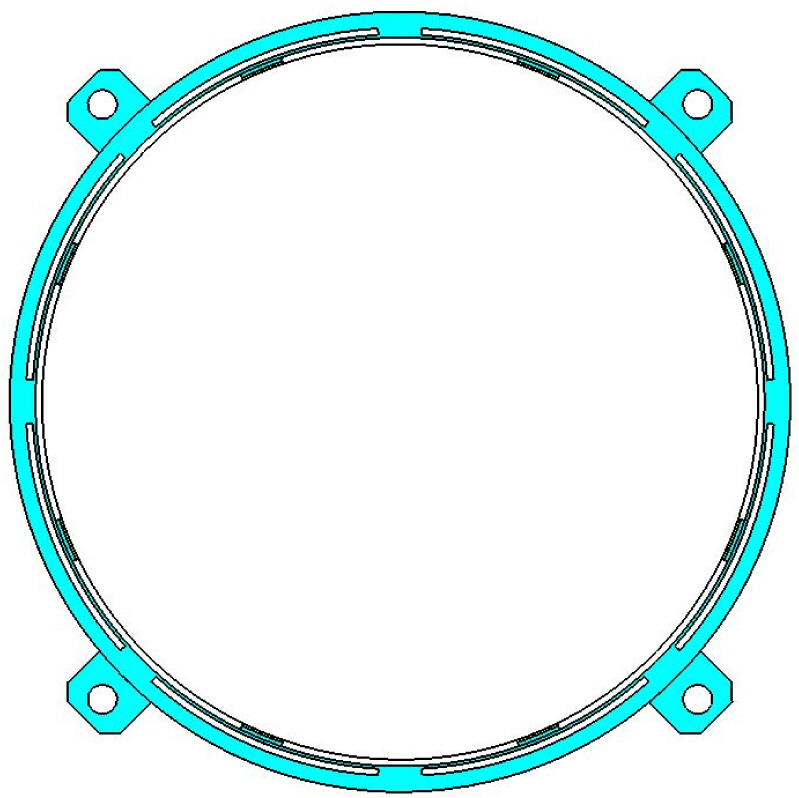
본 연구의 목표는, Fig. 1과 같이 구성된 광학미러 조립체에 대하여, Fig. 2의 Lee 등의 연구^[7]에서 제시 된 광학미러용 마운트에 비하여 제작성이 개선된 마운트 최적설계안을 얻는 것이다. 마운트의 형상은 외경 118.4 mm, 내경 110 mm, z 방향 높이 10 mm로서, 원주방향으로 45° 등간격으로 위치하는 8개의 마운트 돌출부에서 본딩재로 광학미러와 결합된다. 기존의 연구에서 위상최적화 기법을 이용하여, 열변형을 억제하여 광학미러의 파면오차를 줄이면서, 1 kHz 이상의 1차 고유진동수를 갖는 최대한 단순화된 형태의 유연힌지 마운트를 설계하였다. 그러나, 기존의 연구에서 도출된 유연힌지는 스플라인 형상으로서, 도면 작성 및 제작이 용이하지 못하며 제작성을 개선하기 위해서 설계를 단순화하면 광학 성능이 저하되는 문제가 있다. 본 연구에서는, 기존의 연구^[7]에서 사용된 마운트의 외경, 내경, 높이와 동일한 치수를 제약조건으로 하되, 마운트에 폭 1 mm의 1자형 슬롯을 가공함으로써 쉽게 제작될 수 있는 일체형 유연힌지를 갖는 마운트를 반응표면법을 활용하여 설계하고자 한다.

Fig. 1.

A schematic drawing of an optical mirror assembly

Fig. 2.

One quarter shape of optical mirror mount from the topology optimization of the previous research^[7]

Table 1은 본 연구의 광학미러 조립체를 구성하는 부품별 재료 물성치이다. 마운트에는 비강성이 크고 열팽창이 적은 티타늄 합금(Ti-alloy)을, 광학미러에는 열팽창이 적은 상용 글라스 세라믹인 Zerodur^® 를, 광학미러와 마운트를 결합하는 본딩재는 MIL-A-46111 규격의 에폭시 소재를 사용한다. 마운트의 유연힌지 치수 최적설계 목표는 광학미러 조립체의 1차 고유진동수가 1 kHz 이상으로 유지되면서, +60 ℃의 고온 및 –32 ℃ 및 저온 조건에서 광학미러의 파면오차가 최소화되도록 하는 것이다. 광학미러, 본딩재, 마운트로 구성된 광학미러 조립체에 대한 1 kHz 이상의 1차 고유진동수 요구조건은 광학미러 조립체가 장착되는 상위의 광집속 구동시스템의 구동 응답 성능을 만족하기 위해서 요구된 값이다. 유연힌지가 구현되지 않은, 원통 형태의 마운트가 적용된 광학미러 조립체의 1차 고유진동수는 1,354 Hz였으며 z방향으로의 굽힘 모드가 발생하였다. 따라서, 광학미러의 파면오차를 축소하기 위해서 마운트의 강성을 감소시킬 여유가 있다.

Table 1.

Mechanical properties used to design the optical mirror assembly

3. 연구 수행 방법

기존의 연구로부터 도출된 Fig. 2의 유연힌지 마운트 형상은, 광학미러와 마운트 연결부에서 광학미러의 반경 방향 열변형을 흡수할 수 있도록, 마운트의 반경 방향 유연성을 증대시킨 형상이다. 동일한 설계 개념으로서, 본 연구에서는 마운트의 광학미러 연결부에 사각형 단면의 단순 지지보(simply supported beam) 형상의 일체형 유연힌지를 적용함으로써, 기존의 연구와 동등한 성능을 가지면서 제작성을 개선시키고자 한다.

두께 t, 폭 b, 길이 L의 단순 지지보의 유연성(Compliance) C는 식 (1)과 같다. 여기서, δ는 보의 중앙에 가해진 집중하중 F에 대한 변형량이며, C는 길이(L)의 세제곱에 비례하고, 두께(t)의 세제곱과 폭(b)에 반비례한다. 따라서, 마운트의 광학미러 결합부에 1자 형태의 관통형 슬롯을 가공함으로써, 유연성이 증대된 단순 지지보 형태의 유연힌지를 갖는 마운트의 설계에 관한 연구를 수행하였다.

본 연구의 수행 방법은 다음과 같다. 우선, Fig. 3과 같이 원주방향으로 등배열된 8개의 관통형 슬롯을 갖는 일체형 유연힌지 마운트의 기준 형상(Reference configuration)을 생성한다. 슬롯의 폭과 길이를 변경함으로써 구현되는 유연힌지의 길이와 두께를 변경시킨 다수의 해석 모델을 생성한다. 열-기계적 하중 조건의 구조해석과 고유모드 해석을 수행하여 광학미러의 파면오차와 1차 고유진동수를 구한다. 파면오차의 설계인자에 대한 반응표면식을 구함으로써, 최적의 유연힌지 설계안을 도출한다. 여기서, 파면오차는 최적화 목적함수로 사용하고, 1차 고유진동수는 유효 설계범위(Feasible domain)를 벗어나는지 여부를 확인하는 용도로 사용한다.

Fig. 3.

Reference configuration of monolithic flexure hinge mount for optical mirror

3.1 유연힌지 기준모델 및 설계인자 설정

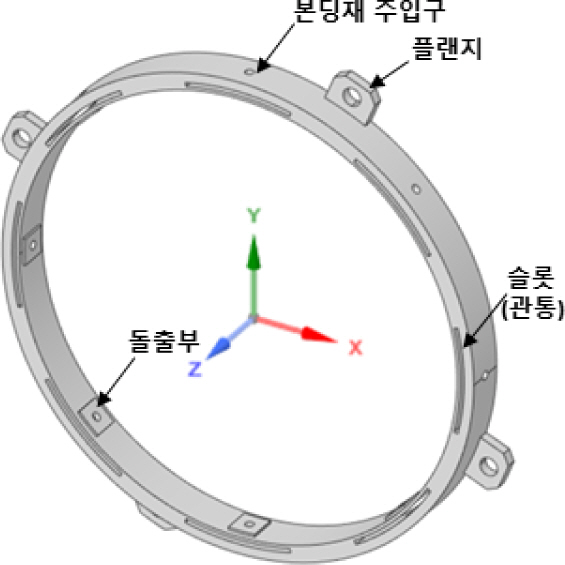
Fig. 3의 유연힌지가 적용된 마운트의 기준모델에 대한 설계 개념은 다음과 같다. 광학미러를 안정적으로 고정하면서, 접착면적이 균일하게 배분되어서 열응력이 광학미러로 전파되는 영향을 줄이도록, 마운트는 45° 등간격으로 8개소의 결합부를 갖는다. 마운트의 결합부 중앙에 외부로부터 본딩재를 주입할 수 있는 주입구를 형성시킨다.

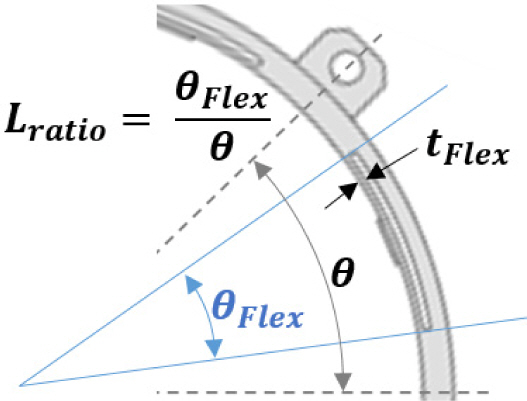
광학미러 조립체의 1차 고유진동수가 1 kHz 이상인 범위 내에서, 유연힌지의 유연성을 최대화하도록, Fig. 4와 같이 유연힌지의 길이와 두께 L_ration, t_Flex 2개의 설계인자를 설정하였다. 여기서,L_ratio는 마운트의 원주 길이에 대한 유연힌지의 길이 비로서, 원호의 중심각 비와 동일하다. L_ratio는 0.6, t_Flex는 0.8 mm가 되도록 기준모델을 생성하였다.

Fig. 4.

Design parameters for flexure hinge

3.2 파면오차 해석

광학미러, 마운트, 본딩재로 구성된 광학미러 조립체에 대하여 유한요소해석을 통해서 광학미러 표면의 변형을 계산하여 파면오차 해석을 수행하는 절차에 대하여 기술한다.

경계조건은 다음과 같다. 마운트의 원주 상에 90° 등간격으로 배치된 4개의 플랜지 구멍을 구속하고, 광학미러 조립체 전체를 저온 –43 ℃, 고온 +50 ℃의 온도 조건을 개별 해석 조건으로 부여한다. 광학미러의 자중을 고려하기 위해서 z 방향으로 1 g의 중력가속도를 인가한다. 저온 및 고온 각각의 조건에 대한 구조해석 결과로부터 광학미러 표면의 모든 절점들의 z 방향 변위 u_z를 추출한다.

u_z를 식 (1)과 같이 n차의 Zernike 다항식으로 근사하여 극좌표 기준으로 ϕ(r,θ)로 표현한다^[8]. 여기서, a_j, Z_j(r,θ)는 반사면 변위의 j차 극좌표 기준 Zernike 다항식 계수 및 기저함수값이다. Zernike 다항식을 구성하는 기저함수는 식 (2)와 (3)으로 정의된다.

(1) ϕ(r,θ)=∑j=1najZj(r,θ)

(2) Zj={n+1Rnm(r)2cos⁡mθ,j= even ,m≠0n+1Rnm(r)2sin⁡mθ,j=odd,m≠0n+1Rnm(r),m=0m≤n,n−|m|= even 

(3) Rnm(r)=∑s=0(n−m)/2(−1)s(n−s)!rn−2ss![(n+m)/2−s]![(n−m)/2−s]!

Zernike 다항식의 1차에서 5차까지의 기저함수의 모드 형상을 Table 2에 도시하였다.

Table 2.

The first 5 modes from Zernike polynomials

Zernike 다항식으로 근사된 변위 ϕ(r,θ)와 실제 계산된 변위 u_z의 오차 e의 제곱합 e²는 식 (4)와 같으며, e²를 최소화하는 a_j를 최소제곱법으로 구한다.

(4) e2=∬Ω(uz−ϕ)2dΩ

광학미러의 변형 성분 중 z축 방향 이동(Piston), x 및 y축에 대한 회전(Tilt) 등의 저차 모드는 제어시스템에서 보정이 가능하므로, 식 (5)와 같이 1차 이동(Piston) 모드와 2∼3차 회전(Tilt), 4차 초점 이탈(Defocusing) 모드는 제외하여 광학면의 변형을 재계산한다. 식 (5)에서 제외되는 차수 N_a는 일반적으로 강체모드까지인 3 또는 초점 이탈(Defocusing) 모드까지 포함한 4로 한다. 식 (6)으로 강체모드가 제거된 변형성분에 대한 광학미러 반사면 요소의 면적 A에 대한 제곱평균제곱근(RMS, Root Mean Square)으로 파면오차(WFE, Wavefront Error)는 정의된다.

(5) u^n=uz−∑j=1NCajZj

(6) WFERMS=1A∬Ω(u^n)2dΩ

3.3 고유모드 해석

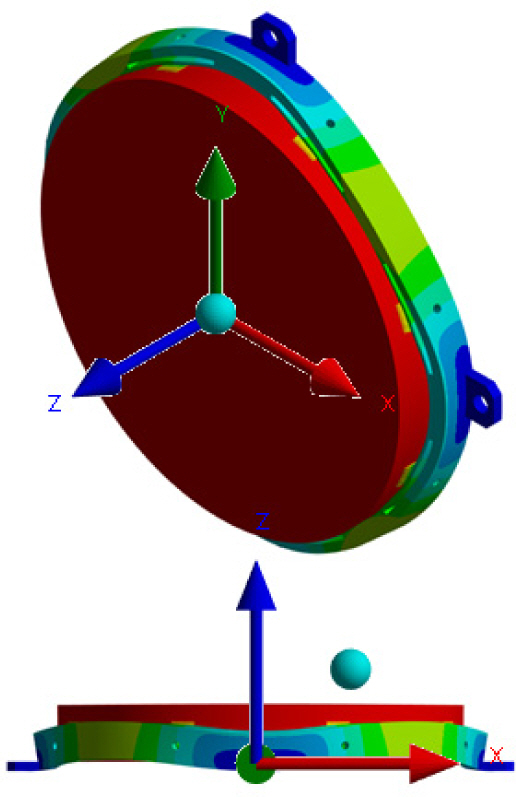
광학미러 조립체의 유한요소 모델을 이용하여 고유모드 해석을 수행하는 절차 및 결과에 대하여 기술한다. 광학미러, 본딩재, 마운트로 구성된 광학미러 조립체에 대하여, Fig. 3에 도시된 마운트의 플랜지 4개의 구멍을 구속한 조건에서 고유모드해석을 수행한다. 사용된 재료 물성치는 Table 1과 같다. 고유모드 해석 결과, 광학미러 조립체 기준모델은 Fig. 5와 같이, 1차 고유진동수 1,327 Hz에서 z 방향으로의 굽힘 모드가 지배적으로 나타났다. 이는 슬롯이 가공되지 않은 원통 형태의 마운트가 적용된 광학미러 조립체의 고유모드와 유사하였다. 반경방향의 강성에 지배적인 인자인 유연힌지의 두께와 길이에 대한 작은 변화는 굽힘 모드인 1차의 고유진동수에 크게 영향을 미치지 않을 것으로 가정하였으며, 해석을 통하여 이를 확인하였다. 광학미러 조립체의 1차 고유진동수가 1 kHz 이상이 될 수 있는 설계 인자의 범위는 설계인자 값을 변경한 몇 가지 해석 모델에 대한 고유모드 해석을 통해서 실험적으로 설정하였다.

Fig. 5.

1 ^st mode shape of reference model for optical mirror assembly

3.5 반응표면법을 이용한 최적화

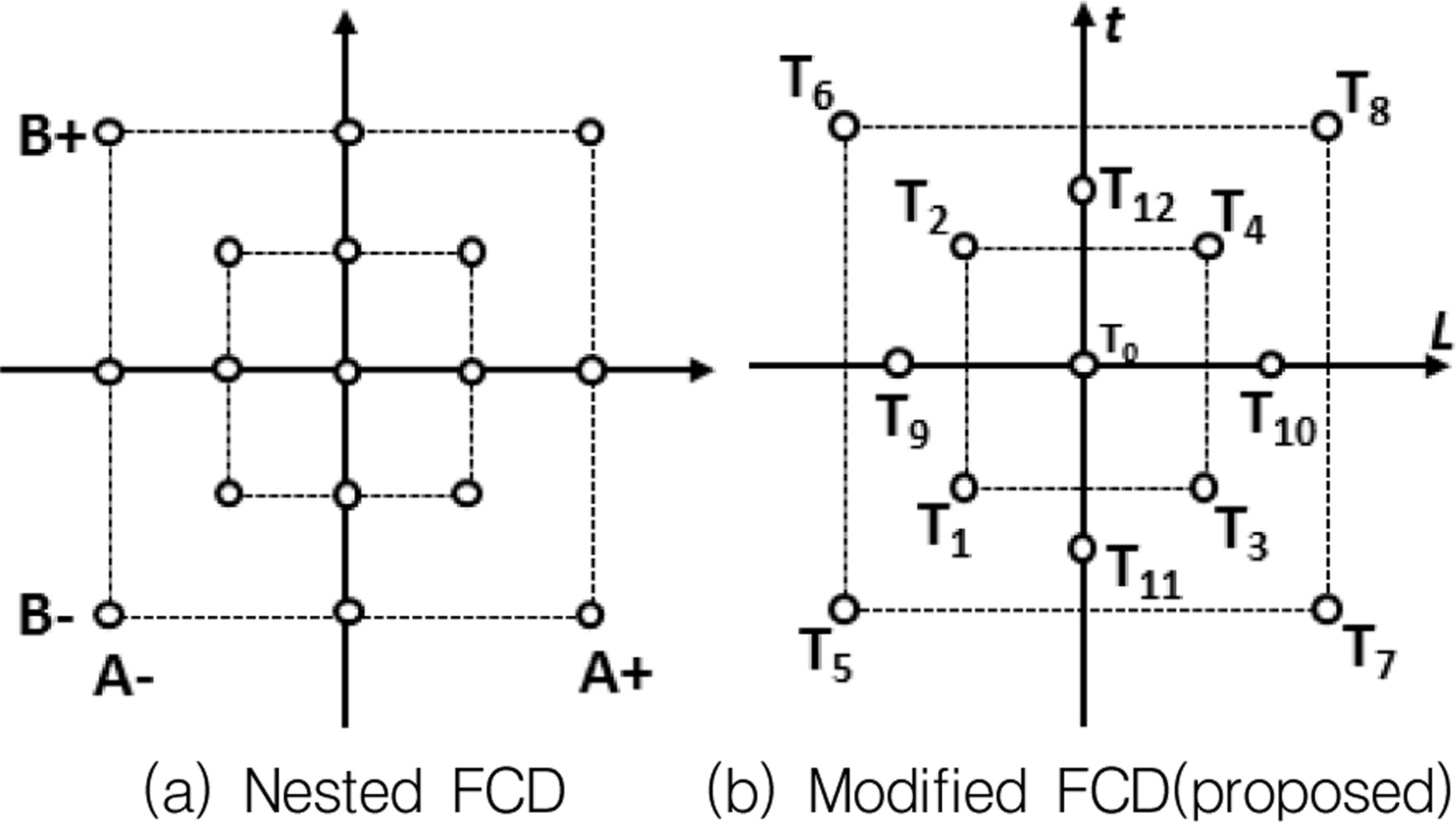
반응표면법(RSM, Response Surface Method)은 여러 개의 설계 인자 X_i에 대한 반응인자 Y의 영향을 다항식 형태로 근사하여 분석하는 실험계획법의 일종이다. 완전요인배치법에 비해 실험 횟수를 감소시키고 2차 다항식 형태의 회귀반응식을 얻을 수 있는 실험계획법으로서 Box와 Wilson(1951)에 의해 제안된 중심합성계획법을 토대로 하여, Landman 등은 풍동실험을 효과적으로 계획하기 위해서, 3차 다항식 형태로 근사할 수 있는 중첩 면심 중심합성계획법(Nested Face Centered Design)을 제안하였다^[9]. Fig. 6(a)와 같이, 2개의 설계 인자에 대한 Nested FCD를 적용하려면 설계점은 총 17개가 필요하다.

Fig. 6.

design points for Nested FCD

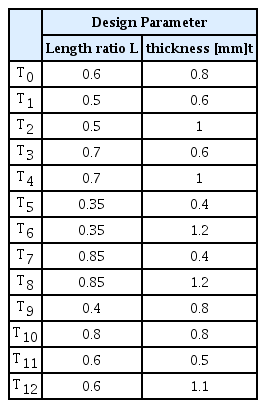
파면오차 f를 반응인자로 하고, L, t 2개의 설계 인자에 대하여 3차 다항식 형태의 반응표면식을 근사하기 위해서 중첩 면심 중심합성계획법를 활용한다. 다만, 각 설계점으로부터 생성된 모델에 대한 유한요소해석에 소요되는 시간을 절감하기 위해서, 본 연구에서는 Fig. 6 (b)와 같이 중첩 면심 중심합성계획법의 설계점의 일부 위치를 변형함으로써, 13개의 설계점으로 축소하는 시도를 하였다. 중심점에서의 설계인자는 L = 0.6, t = 0.8 mm로 하였으며, 각 설계점에서의 인자 값은 Table 3과 같다.

Table 3.

Design parameter values for each design points

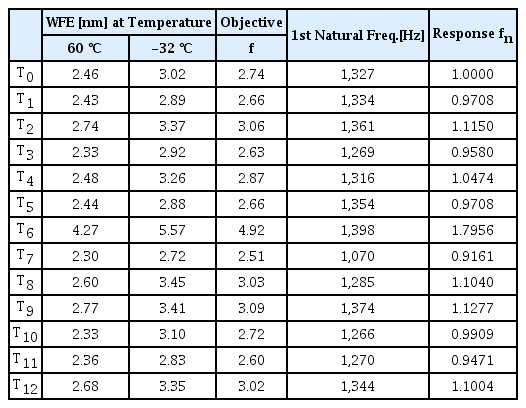
각각의 설계점에서의 인자 값을 적용하여 생성한 광학미러 조립체 모델에 대해 얻은 파면오차와 1차 고유진동수 값은 Table 4와 같다. L이 증가할수록, t가 감소할수록 마운트의 강성이 낮아지므로, 파면오차와 1차 고유진동수가 감소하는 경향을 보인다. 고온과 저온 조건 각각에서 얻은 파면오차의 평균값 t를 T₀(Reference model)에 대하여 식 (8)과 같이 정규화(Normalize)한 f_n을 반응값으로 선정하였다. 여기서, f_i는 설계점 T_i에서의 해석값을 의미한다.

Table 4.

Analysis results for each design points

(8) fni=fi/f0

반응값 f_n에 대한 3차의 반응표면식은 식 (9)와 같으며, MATLAB의 <fitlm> 함수를 이용하여 식 (10)의 회귀 계수를 구하였다.

(9) f=∑i=03∑j=03aijLjti

식 (10)에서의 회귀 계수 a_jj는 p-Value가 0.5 이상이 될 경우 해당 항은 유의하지 않다고 판단하여 탈락시키고 <fitlm> 함수를 재실행하는 반복계산을 3회 수행함으로써 얻은 값이다. 즉, a₁₃, a₂₂, a₃₀ 등과 같이 회귀 계수 값이 ‘0’인 항은 p-Value 가 0.5 이상이어서 탈락되었다.

(10) fn=a00+a01L+a10t+a11Lt+a02L2+a20t2+a12L2t+a21Lt2+a03L3+a30t3a00=8.940,a01=−24.461,a10=−4.858,a11=9.500,a02=26.709,a20=0.765a12=−5.278,a21=−0.730,a03=−9.680

위와 같이 구한, 광학미러 조립체 모델에 대한 광학미러 파면오차의 회귀 반응식은 R² 가 0.985로서 1에 가까우며, 제곱평균제곱근 오차(RMSE, Root Mean Square Error)는 0.048이다. 13개의 각 설계점에 대한 해석결과 f_n과 회귀반응식에 L, t 값을 대입하여 계 산된 결과 fn∗에 대한 오차는 Table 5와 같다. 최대 오 차는 T₁에서 발생하며, 6.4 % 이다. T₀와 T₄에서의 fn∗의 값 차이는 0.047로서, 제곱평균제곱근 오차 보다 작으므로, 반응표면식을 이용하여 근사적으로 도출된 최적설계안에 대하여 파면오차 해석을 통해서 확인하는 과정이 필요하다.

Table 5.

Error analysis results

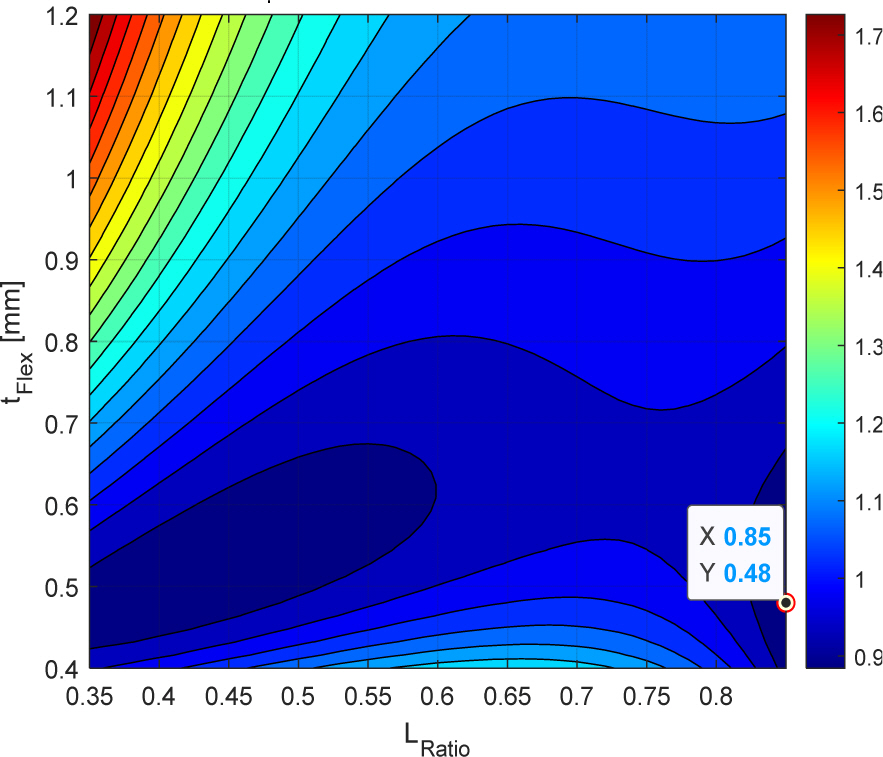
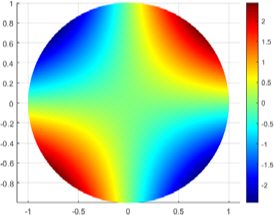
Fig. 7은 L, t 값에 대한 회귀 반응식 fn∗의 등고선도이다. 등고선도에서 [T, t]가 [0.85, 0.48]일 때, fn∗ 이 최소이다.

Fig. 7.

Contour plot of response function fn∗ for L_ratio and t_Flex

4. 최적설계 결과 검토

회귀 반응식에 설계인자 [L, t]의 최적점 [0.85, 0.48] 를 대입함으로써, 0.884의 반응값 fn∗ 을 얻었다. 앞 절 의 오차 분석 결과에서와 같이, 회귀 반응표면식을 이용한 반응값은 5 % 정도의 오차를 나타내므로, 실제 해석을 통해서 결과를 검토한다. Fig. 8의 최적설계 형상에 대하여 유한요소해석을 통해서 파면오차와 1 차 고유진동수를 계산하여 반응표면식의 최적값과 비교함으로써, 최종적으로 최적설계 결과를 확인한다.

Fig. 8.

Optimum design from this research

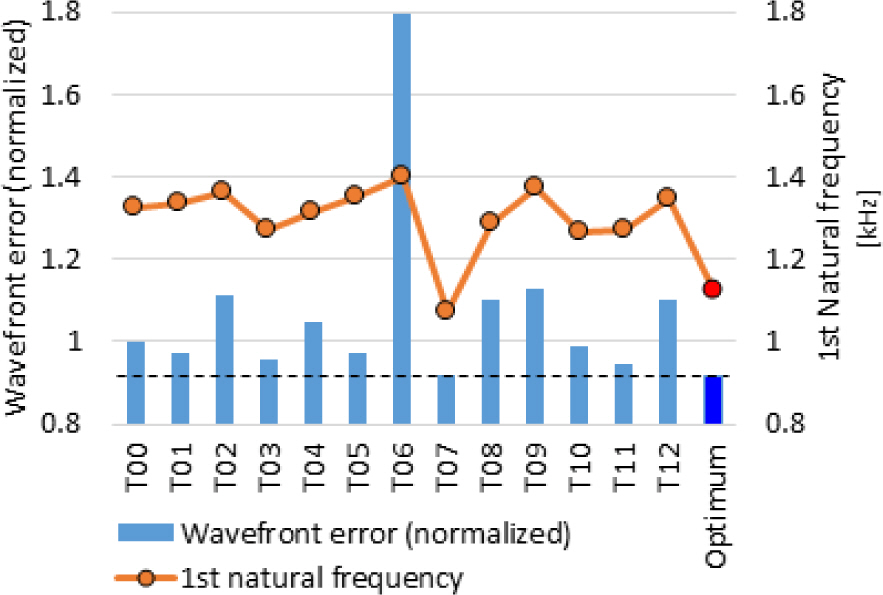
13개의 설계점에서의 모델과 도출된 최적설계 안에 대한 파면오차 및 고유진동수를 Fig. 9에 비교하였다.

Fig. 9.

Comparison of analysis results for design points and optimum design

최적설계안에 대한 해석을 통해서 얻은 파면오차는 +60 ℃ 고온조건에서는 약 2.3 nm, - 32 ℃ 저온조건에서는 약 2.72 nm로서, f_n은 0.916으로서, 회귀 반응식으로 예측한 값 0.884 대비 약 3.6 % 의 오차를 보인다. Fig. 9에서와 같이, 최적설계안의 파면오차는 T07과 유사한 수준의 낮은 값을 보이지만, 1차 고유진동수는 1,127 Hz로서 T07의 1,070 Hz 대비 5 % 높다.

따라서, 본 연구에서 도출한 최적설계안은 의미있는 결과라고 판단한다. 또한, 기존의 연구^[7]에서 도출된 Fig. 2의 마운트에 대한 +60 ℃ 고온조건에서의 파면오차 2.87 nm 보다 우수한 광학 성능을 가지면서 단순한 형상의 마운트 설계를 얻었다.

위와 같이, 본 연구의 목표인 1 kHz 이상의 1차 고유진동수를 갖는 범위 내에서, 파면오차를 최소화하는 제작성이 향상된 유연힌지 마운트 형상을 도출하였다.

5. 결 론

광학미러 조립체에 대한 파면오차 해석과 고유모드해석 및 반응표면법을 활용하여, 기존의 연구에서 도출된 유연힌지 일체형 마운트에 비해서 제작성 우수한 단순한 형태의 광학미러용 일체형 유연힌지 마운트의 최적설계를 도출하였으며, 다음의 결과을 얻었다.

본 연구에서 도출된 일체형 유연힌지 구조의 광학미러 마운트를 제작하여 실험을 통해서 성능을 확인하는 연구가 수행될 예정이다.

Article information Continued