다중/이종 무인전투체계를 위한 효율적 과업-자원 할당 기법
Efficient Task-Resource Matchmaking Technique for Multiple/Heterogeneous Unmanned Combat Systems
Article information
Trans Abstract
In the future battlefield centered on the concept of mosaic warfare, the need for an unmanned combat system will increase to value human life. It is necessary for Multiple/Heterogeneous Unmanned Combat Systems to have suitable mission planning method in order to perform various mission. In this paper, we propose the MTSR model for mission planning of the unmanned combat system, and introduce a method of identifying a task by a combination of services using a request operator and a method of allocating resources to perform a task using the requested service. In order to verify the performance of the proposed task-resource matchmaking algorithm, simulation using occupation scenarios is performed and the results are analyzed.
기 호 설 명
UGV : Unmanned Ground Vehicle
UAV : Unmanned Aerial Vehicle
MTSR Model : Mission-Task-Service-Resource Model
SOT : Sequence of Tasks
1. 서 론
Mosaic Warfare 개념[1] 중심의 미래전장에서는 전투 효과도 증대 및 인명 중시 측면에서 무인전투체계의 필요성이 대두되고 있다. 특히 무인전투체계를 활용한 미래 지상전의 전투 형태는 저비용의 소형화된 다량의 무기체계 간 조합이 가능하고, 전장의 요소에 즉각적으로 반응하기 위한 네트워크 중심전(Network Centric Warfare)에 적합한 소규모 부대 중심의 형태로 발전하게 될 것이다. 이러한 소규모 부대 단위의 무인전투체계를 활용하여 단순한 지뢰/폭발물 처리에서 정찰, 감시, 화력지원 및 점령과 같은 복합임무[2,3]까지 다양한 분야의 임무수행을 위해서는 소규모 부대 단위에 적합한 임무계획[4,5] 방안이 요구된다. 소규모 부대 단위의 무인전투체계 구성은 다양한 형태의 UGV 및 UAV 로 이루어지며, 이를 위한 임무계획 기법은 다중/이종 로봇을 대상으로 과업(Task)을 식별 및 구성하여 수행 가능한 자원(Resource)에 할당할 수 있어야 한다. 전통적인 임무계획 기법[6,7]은 상위 제대로부터 임무를 수령하고, 임무를 수행할 자원을 결정한 후, 임무분석을 통해 과업 및 과업절차를 생성하는 과정으로 이루어진다. 특히 단일로봇의 임무계획은 로봇이 수행해야 할 과업을 생성하여, 수행 시간축상에서 과업의 실행순서를 스케줄링하는 작업으로 정의된다.
본 논문에서는 다중/이종 로봇으로 구성되는 소규모 부대 단위의 무인전투체계의 임무계획을 위해 임무, 과업, 서비스 그리고 자원의 계층으로 임무를 표현하는 MTSR 모델을 활용한다. 또한 MTSR 모델에 기반하여 과업 수행에 요구되는 능력을 의미하는 요구 서비스들의 조합으로 과업을 식별하는 방식과 요구 서비스를 매개체로 각 과업을 수행할 자원들을 결정하는 효율적 과업-자원 할당 기법을 소개한다. 기존 연구에서는 다양한 방식으로 자원할당 문제에 접근하였는데, 특정 매개체를 기준으로 과업-자원 할당을 수행한 연구로는 [4], [8], [9]가 있다. [4]는 과업 수행을 위한 요구성능 및 자원 제공기능을 매개체로 MDLS (Multidimensional Dynamic List Scheduling Method) 기반의 자원할당을 수행하였는데, 할당 매개체로 ‘대공전(AAW)’, ‘대함전(ASUW)’ 및 ‘지뢰개척(MINE)’ 등과 같은 8개 항목을 정의하였다. [8], [9]는 자원이 제공하는 능력을 매개체로 온톨로지 기반의 자원할당을 수행하였는데, 할당 매개체로 [4]에서 정의한 매개체에 ‘기동(Mobility)’, ‘탐지(Detection)’ 및 ‘통신(Communication)’ 등을 추가하여 총 11개 항목을 정의하였다. 자원할당을 위한 매개체의 식별은 기존 논문과 같이 임무장비 단위의 능력이나 성능으로도 가능하지만, 과업의 특성에 따라 ‘지뢰탐지 종류(금속, 비금속)’, ‘지뢰탐지 깊이’와 같이 더욱 특화된 세부능력 단위로 식별할 수 있어야 한다. 본 논문에서는 더욱 상세한 요구성능을 매개체로 과업을 수행할 자원을 결정하는 효율적 자원할당 기법을 제안한다.
제안한 요구서비스 기반 과업-자원 할당 기법의 성능검증을 위해 점령 시나리오를 활용한 자원 매칭 시뮬레이션을 수행하고 그 결과를 분석한다.
2. MTSR 모델 기반의 과업 식별
다중/이종 무인전투체계를 위한 임무계획시스템의 지능화/자동화를 위해서는 임무계획의 단계를 알고리즘상에서 표현할 수 있는 모델[8]이 요구된다. 본 장에서는 기존의 MTSR 임무표현 모델을 재정의하며, 모델에 기반하여 요구연산자를 활용한 단위 서비스의 조합으로 과업을 식별하는 방식을 소개한다.
2.1 MTSR 임무표현 모델
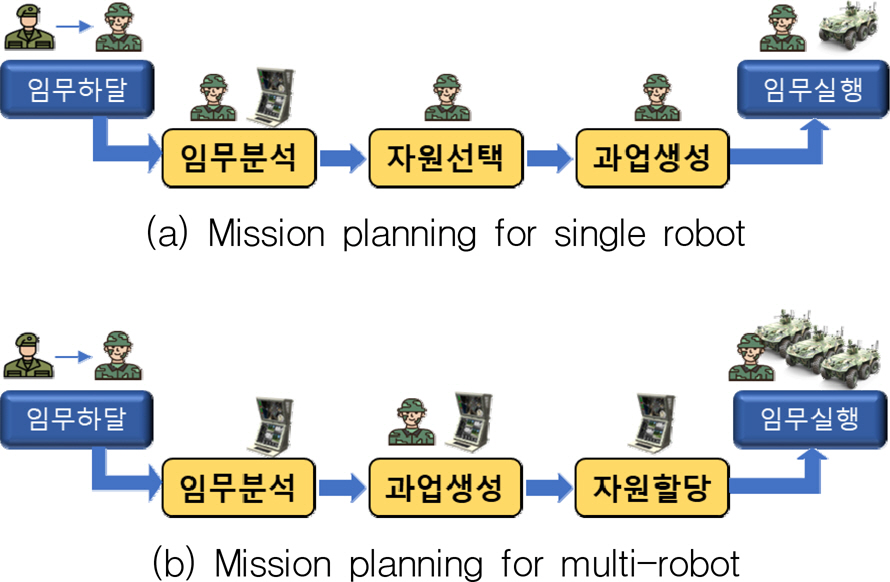
Fig. 1 (a)에 보이는 기존 단일로봇의 임무계획시스템은 상위 제대로부터 부여받은 임무를 운용자가 분석 후, 임무를 수행할 단일로봇을 선택하고 해당 로봇이 수행할 과업을 생성하는 방식으로 동작한다[6]. 이러한 방식은 필요한 과업 및 자원의 수가 증가할수록 운용자의 임무 부하가 급격히 늘어나게 되며, 또한 운용자의 능력이 임무계획 성공 여부의 주요 변수로 작용하는 문제점이 있다. 다중/이종 로봇을 운용하기 위한 임무계획시스템은 Fig. 1 (b)와 같이 하달받은 임무를 분석하여 수행할 과업을 생성한 후, 각 과업을 수행할 자원을 자동으로 할당할 수 있는 과업-자원 할당 기법이 요구된다[9].
본 논문에서는 과업-자원 자동할당을 포함하는 임무계획의 지능화를 위한 임무표현 모델로, 기존의 MTSR 모델[9]을 채용하여 다중/이종 무인전투체계의 임무계획에 적합하도록 과업 및 서비스 계층을 새롭게 정의하여 사용한다. 재정의된 MTSR 임무표현 모델은 임무를 임무, 과업, 서비스 그리고 자원의 계층으로 표현한다. 임무는 상위 제대로부터 로봇 부대에 하달되는 군사적 목표를 의미하며, 임무목표 달성을 위한 과업들로 구성되는 과업절차(Sequence of Tasks)의 형태로 표현된다. 과업은 자원이 실행 가능한 작업 단위의 일로 정의되며, 과업 수행에 요구되는 서비스의 조합으로 식별된다. 서비스의 정의는 과업 관점에서는 과업 수행에 요구되는 능력이며, 자원 관점에서는 자원이 제공 가능한 기능을 의미한다. 마지막으로 자원은 특정 부대가 보유하고 있는 모든 로봇의 집합으로 정의된다. 재정의된 MTSR 모델의 가장 큰 특징은 서비스 계층을 식별함으로써 요구 서비스의 조합으로 다양한 과업 생성이 가능하다는 점이다. 기 개발 완료한 국방 로봇인 견마로봇[6,10], 경전투로봇[11] 및 기지방호로봇[12]과 같은 단일로봇은 보유 임무장비의 제한으로 인해 다양한 과업 수행이 불가능하여, “대기”, “이동”, “지뢰탐지”, “감시”, “이동감시” 및 “화생방탐지”와 같은 기 식별된 유한개의 과업들의 조합만으로도 임무계획이 가능하다. 하지만 다중/이종 로봇으로 구성된 무인전투체계의 경우 다양한 임무 수행 능력이 요구되며 이를 위해서는 요구 서비스의 조합으로 다양한 과업을 생성할 수 있는 MTSR 모델 기반의 임무계획을 필요로 한다.
2.2 요구서비스 기반의 과업 식별
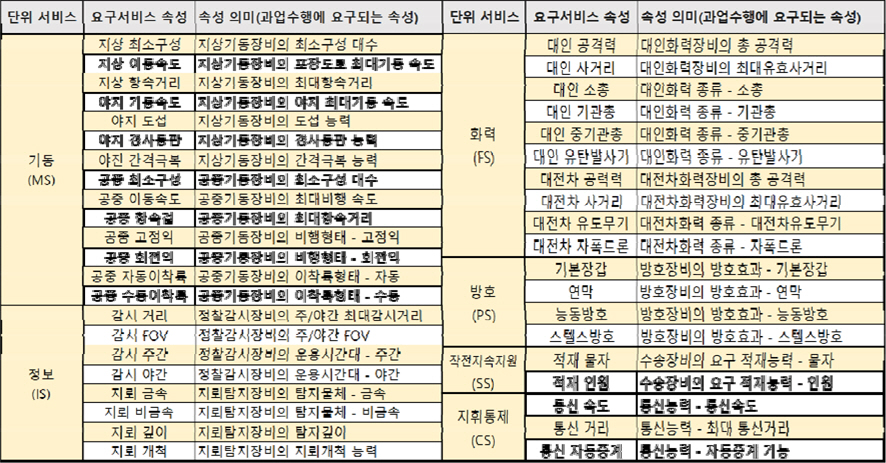
과업은 임무 수행의 작업 단위로서, 과업 수행에 요구되는 능력들을 조합하여 생성할 수 있다. 과업 수행에 요구되는 ‘능력’이란 로봇에 장착된 임무장치의 ‘기능’과 같은 의미이다. 이러한 요구능력 혹은 제공기능을 서비스로 정의하는데, 본 논문에서의 서비스는 Table 1과 같이 군의 6대 능력을 기반으로 모델링 하였다. 특히 기동(Maneuver Service), 정보(Information Service), 화력(Fire Service), 방호(Protect Service), 작전지속지원(Sustain Service) 및 지휘통제(Communication Service)는 단위 서비스(Unit Service)로 정의되며, 이는 다양한 로봇들이 보유한 임무장비 기반의 기능을 군의 6대 능력기반으로 목록화한 개념이다. 각 단위 서비스는 해당 능력의 세부 기능인 서비스 속성을 가진다. Fig. 2와 같이 ‘적소대 격퇴’ 과업을 식별하는 경우, 과업 수행에 요구되는 ‘기동’ 및 ‘화력’ 단위 서비스를 조합하여 과업을 생성한다. 동일한 단위 서비스를 요구하는 과업 간의 차별성은 그 과업을 수행하는 세부적인 방법과 세부적인 요구 능력(기능)의 차이에서 발생하게 된다. 과업 수행 그룹의 규모와 이동대형 그리고 적 발견 시 대응정책(공격우선, 회피우선) 등과 같은 특정 과업을 수행하는 세부적인 방법은 ‘과업 속성’으로, 요구되는 최대기동 속도, 야지기동 능력 보유 여부, 요구 공격능력(대인화력, 대전차화력) 및 최대유효사거리 등과 같은 세부적인 요구 능력(기능)은 ‘요구서비스 속성’으로 정의한다. 요구서비스 속성이 과업-자원 할당을 위한 매개체로 사용되는 반면, 과업 속성은 과업수행 방안에 필요한 정보의 운용자 제공에 활용된다.
2.3 서비스 요구연산자
2.2절에서 과업 생성은 과업 수행에 요구되는 단위 서비스의 조합으로 이루어진다고 정의하였다. 이러한 단위 서비스의 조합은 서비스 요구연산자를 통해 이루어지며, 서비스 요구연산자는 동시만족(⊗) 및 분담만족(⊕)으로 구성된다. 동시만족 의미는 과업 수행에 단위 서비스 A와 단위 서비스 B를 동시에 제공 가능한 자원(들)이 필요하다는 의미이다. 또한 분담만족 의미는 과업 수행에 단위 서비스 A 및 단위 서비스 B를 분담하여 제공 가능한 자원(들)이 필요하다는 의미이다. 여기서 ‘분담제공’은 하나의 자원이 두 서비스를 동시에 제공하거나, 혹은 여러 자원이 두 서비스를 분담하여 제공할 수 있다는 의미이다.
Fig. 3은 GUI 상에서 과업을 식별하기 위한 절차를 보여준다. 운용자는 부여받은 임무에 적합한 과업절차 (SOT)를 생성하고, 과업별로 과업 수행에 필요한 단위 서비스를 요구연산자를 활용하여 부여한 후, 과업 속성값 및 요구서비스 속성값을 입력한다. Fig. 3에 보이는 과업 ‘Task2’의 단위 서비스 조합에 사용된 요구연산자는 수식 (1)과 같다. GUI 상에서 요구연산자 ⊗는 ‘서비스 요구연산자’를 표현하는 Tree 구조에서 한 단계 하위레벨로, 요구연산자 ⊕는 동일레벨로 표현된다. Fig. 3의 ‘서비스 요구연산자’ Tree 구조에서 ‘지휘통제’ 노드는 ‘기동’ 노드의 자식노드로 두 노드는 동시만족(⊗) 요구연산자 관계이며, ‘정보’ 노드와 ‘화력’ 노드는 동일레벨 노드로 분담만족(⊕) 요구 연산자 관계이다. 수식 (1)의 의미는 ‘Task2’에 할당되는 자원(들)은 단위 서비스 ‘기동’과 ‘지휘통제’와 관련된 요구서비스 속성을 반드시 만족하여야 하며, 단위 서비스 ‘정보’와 ‘화력’과 관련된 요구서비스 속성은 다수의 자원이 분담하여 만족 가능하다는 의미이다. 하지만 분담만족에 관여하는 모든 자원은 반드시 단위 서비스 ‘기동’과 ‘지휘통제’ 관련된 서비스 속성을 만족해야 한다.
3. 임무계획을 위한 과업-자원 자동할당
운용자는 서비스 요구연산자를 활용하여 단위 서비스들의 조합으로 과업을 생성하고, 해당 과업에 과업 속성 및 서비스 속성을 부여한다. 임무계획의 마지막 단계는 각 과업을 수행할 자원들을 자동으로 결정하는 과업-자원 매칭 단계이다. 본 장에서는 과업-자원 결정 문제를 convex 최적화 문제로 표현하고, 주어진 제한조건들을 만족하는 과업-자원 할당 기법을 소개한다.
3.1 과업-자원 할당 문제 정의
로봇 부대가 보유하고 UGV와 UAV를 포함한 n개의 가용자원을 의미하는 배열 R은 수식 (2)와 같이 표현되며, rn은 n번째 가용자원(robot)을 의미한다. 운용자가 작성한 과업절차에 포함된 k개의 과업을 의미하는 배열 W는 수식 (3)과 같이 표현되며, tk는 k번째 과업(task)을 의미한다. 수식 (4)는 6종의 단위 서비스에서 식별된 m개의 서비스 속성을 의미하는 배열 S를 표현하며, 배열 S는 서비스 속성의 전체집합 개념으로 cm은 m번째 서비스 속성을 의미한다. 모든 자원이 제공 가능한 기능을 의미하는 자원-서비스 테이블 RS는 수식 (5)와 같이 정의되며, 첫 행의 의미는 자원 r1이 제공 가능한 모든 서비스 속성들의 값이다. RS는 로봇 부대에 배치된 모든 자원의 임무장비를 기준으로 사전 설정되는 테이블이다. dti는 자원의 현재위치에서 과업 ti가 수행되는 위치까지의 지리적 거리로, 가능하면 과업 수행 위치에 근접한 자원을 할당하기 위해 포함된다. 또한 운용자가 자원할당의 매개체로 제공하는 수식 (6)의 과업-서비스 테이블 WS는 과업 수행에 요구되는 능력을 의미하며, 첫 행의 의미는 과업 t1의 수행을 위해 요구되는 모든 서비스 속성들의 값이다. 마지막으로 수식 (7)의 P는 convex 최적화 문제에서 해결해야 하는 최적화 변수(optimization variable)로 pi 는 특정 과업에 할당된 i번째 자원의 개수를 의미한다.
본 논문의 과업-자원 할당 문제는 과업절차(SOT)상의 i번째 과업 ti에 대하여 운용자가 제시한 요구서비스를 충족하면서 자원의 할당 수량을 최소화하는 P를 찾는 문제로 다음과 같이 정의된다.
3.2 요구서비스 기반 후보자원 추천
과업-자원 할당 알고리즘은 자원-서비스 테이블 RS 로부터 특정 과업의 요구서비스를 만족하는 자원의 최소조합을 찾는 문제이다. 과업의 요구서비스는 서비스 요구연산자를 통한 단위 서비스의 조합으로 생성된다. 자원-서비스 테이블에서 운용자가 식별한 과업 요구서비스를 만족하는 자원들을 선별하여 수식 (9)의 후보자원-서비스 테이블 C를 생성하는 과정을 요구서비스 기반 후보자원 추천이라 정의한다. 후보자원 추천을 적용한 과업-자원 할당 문제는 수식 (10)으로 재정의된다.
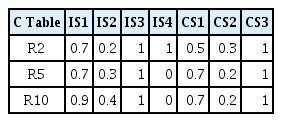
이전 장에서 제시된 서비스 요구연산자를 활용하여 후보자원을 추천하는 과정을 살펴보면 다음과 같다. Table 2는 과업 ‘Task 1’의 수행에 필요한 요구서비스를 식별한 과업-서비스 테이블 WS로 포함 데이터는 정규화 값이다. 서비스 속성 중 ‘IS2(FOV)’ 및 ‘CS2(통신거리)’는 조합속성으로 다수 자원의 조합으로 해당 속성의 요구사항을 만족할 수 있다. Table 3은 모든 가용자원에 대해 자원이 제공 가능한 서비스와의 관계를 보여주는 자원-서비스 테이블 RS이다. ‘정보(IS)’ 단위 서비스 및 ‘지휘통제(CS)’ 단위 서비스에 동시만족(⊗) 및 분담만족(⊕) 요구연산자를 적용하여 해당 요구서비스 조건을 만족하는 후보자원을 추출하여 생성한 후보자원-서비스 배열 C를 Table 4에서 확인할 수 있다.
3.3 과업-자원 할당 알고리즘
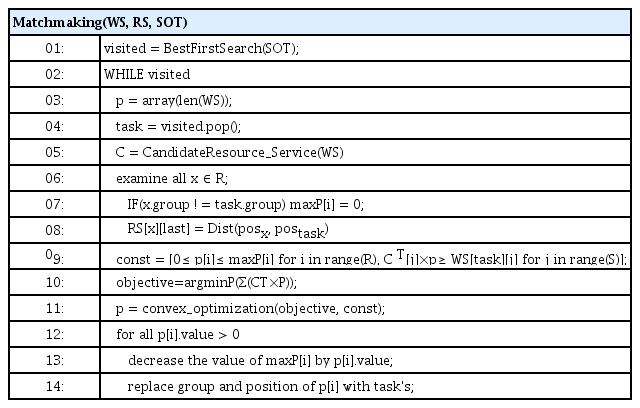
본 논문에서는 과업-자원 결정 문제를 convex 최적화 문제로 표현하고, CVXPY를 활용하여 주어진 제한조건들을 만족하는 과업-자원 할당 기법을 제안한다. CVXPY[13]는 convex 최적화 문제를 위한 파이썬 내장 모델링 언어로, 자동으로 문제를 표준형식으로 변환하고, solver를 호출하여 그 결과를 도출한다. Table 5는 과업-자원간 매칭 알고리즘으로 과업절차(SOT) 그래프, 과업-서비스 테이블 WS 및 자원-서비스 테이블 RS를 입력받아 과업별 할당 자원 및 개수를 결정한다. 자원할당에 적용되는 제한조건은 네 가지로 다음과 같으며 Table 5의 9번라인에서 정의된다.
첫째 할당된 자원이 제공하는 서비스의 총합은 운용자가 제시한 요구서비스 총량보다 크거나 같아야 한다. 다만, ‘개별 서비스별로 후보 자원들의 조합이 제공하는 해당 서비스의 총합은 운용자가 요구한 해당 요구서비스의 속성값보다 크거나 같아야 한다’라는 Table 5의 9번 라인의 제한조건을 만족하여야 한다. 둘째, 특정 자원 p[i]의 최대 할당 개수는 부대의 보유자원 개수보다 작거나 같아야 한다. 셋째, 자원할당 시 그룹 간 자원할당은 배제된다. 즉, 특정 그룹의 과업에 할당된 자원은 타 그룹 과업으로 재할당 됨이 제한된다는 의미이다. 여기서 그룹이란 동일한 소목적을 가지고 유사한 지역에서 수행되는 과업의 묶음을 의미한다. 마지막으로, 자원할당 시 과업-자원 간 지리적 거리정보를 반영하여 가능한 해당 과업에 근접한 자원을 할당한다. 제한조건 중 maxP[i]의 개수를 통해 자원의 최대할당 개수 문제 및 그룹간 자원할당 배제 문제를 그리고, 배열 RS[][last] 값을 통해 과업-자원간 지리적 거리정보를 매칭에 반영할 수 있다. 여기서 last는 수식 (5)의 dti를 의미한다. Table 5의 5번 라인의 CandidateResource_Servie() 함수는 3.2절에서 언급한 요구서비스 기반 후보자원 추출을 수행한다.
4. 시나리오 기반 자원할당 시뮬레이션 결과
제안한 다중/이종 무인전투체계용 과업-자원 할당 기법의 성능검증을 위해 ‘적 요충지인 항구와 공항을 점령’하는 점령 시나리오를 활용한 자원할당 시뮬레이션을 수행하고 그 결과를 분석한다.
4.1 과업-자원 할당 시나리오
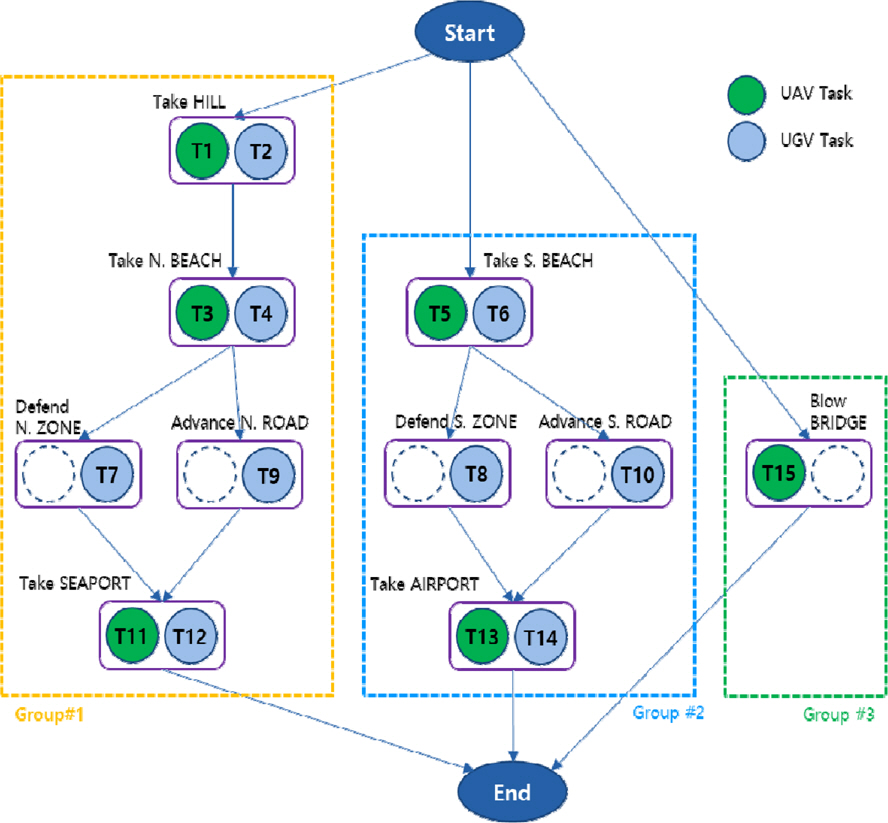
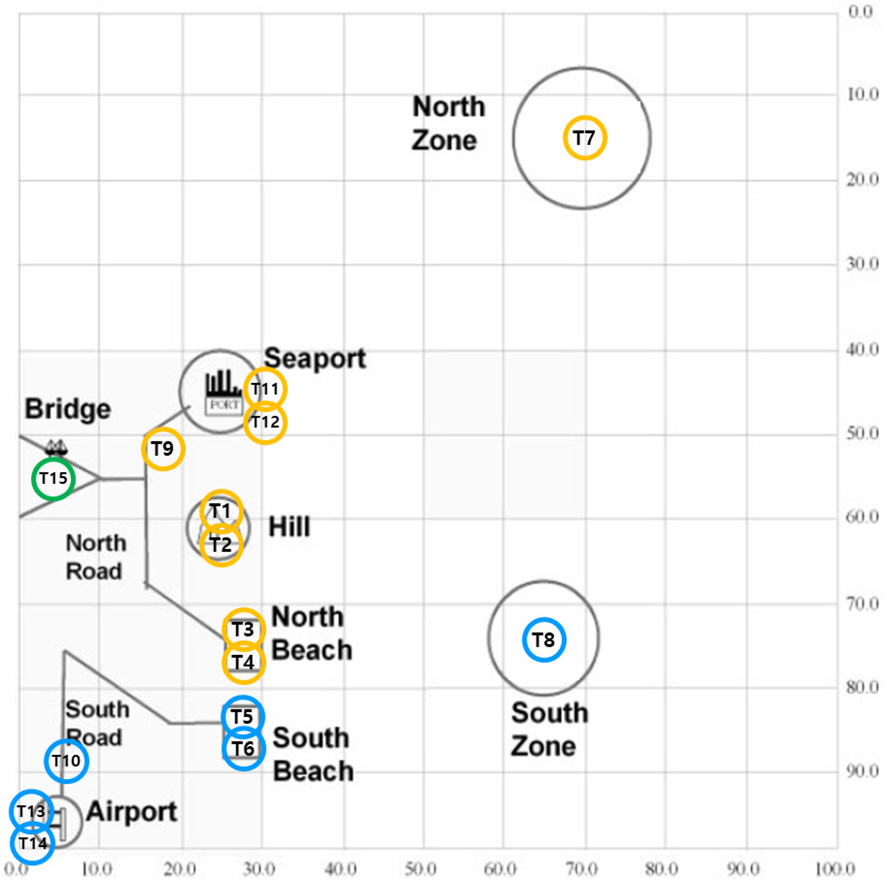
제안한 과업할당 기법의 검증을 위한 시나리오는 “후속부대 침투를 위한 적 요충지인 항구와 공항을 점령”하는 임무[14]이며, 이를 위한 과업절차는 Fig. 4와 같다. 해당 과업절차에는 항구점령 그룹(yellow), 공항점령 그룹(blue) 그리고 다리폭파 그룹(green)과 같은 세 그룹이 존재하며, 그룹은 동일한 소목적을 가지고 유사한 지역에서 수행되는 과업의 묶음을 의미한다. Fig. 5는 과업절차상의 모든 과업이 수행되는 위치를 지도상에 보여준다. 임무가 수행되기 전의 모든 가용자원의 초기위치는 (0, 0)으로 부대 기지로 가정한다.
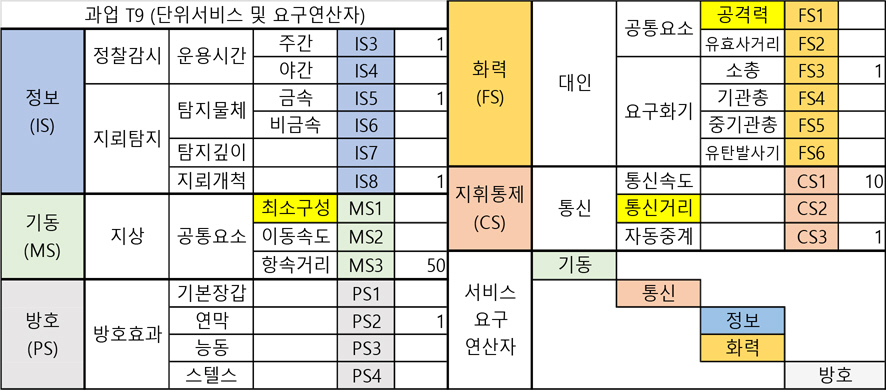
과업을 수행할 자원을 결정하기 위해서는 과업별로 과업 수행에 필요한 단위 서비스를 요구연산자를 활용하여 부여한 후, 요구서비스 속성값 입력이 필요하다. Fig. 6은 총 15개의 과업 중 ‘Advance on North Road’라는 이름의 과업 T9에 대한 요구 단위 서비스, 요구연산자 및 서비스 속성값을 보여준다. 과업 T9를 수행하기 위해 요구되는 단위 서비스는 ‘기동(MS)’, ‘정보(IS)’, ‘지휘통제(CS)’, ‘화력(FS)’ 및 ‘방호(PS)’이며, 그림에 보이는 요구연산자는 수식 (11)로 표현할 수 있다. 노란색으로 표현된 서비스 속성은 3.2절에서 언급한 조합속성을 의미하며, 빈 서비스 속성은 과업 수행에 필수요소가 아님을 의미한다.
4.2 자원 할당 시뮬레이션 결과 및 분석
과업-자원 할당 알고리즘은 과업절차(SOT), 과업-서비스 테이블 및 자원-서비스 테이블을 입력받아, 자원-서비스 테이블에서 자원할당 대상 과업에 대한 요구서비스를 만족하는 자원들을 선별하여 후보자원-서비스 테이블을 생성하고, 대상 과업별로 Table 5의 9번라인에서 정의한 네 가지의 제한조건을 만족하는 자 원의 최소조합을 계산한다. Fig. 7은 점령 임무를 포함하는 시나리오의 자원할당 시뮬레이션 결과로, 과업별로 할당된 자원의 종류 및 개수를 보여준다. 본 시나리오상의 가용자원 R은 서로 다른 서비스를 제공하는 UGV 12대 및 UAV 8대로 구성되며, 동일 기능을 가진 자원 중복은 허용하지 않는다.
과업-자원 할당에 적용되는 네 가지 제한조건 관점에서 점령 시나리오 시뮬레이션을 분석한 결과는 다음과 같다. 첫 번째 제한조건은 할당된 자원이 제공하는 서비스의 총합은 운용자가 제시한 요구서비스 총량보다 크거나 같아야 한다는 것이다. Fig. 6에 보이는 과업 T9의 요구서비스 속성값의 총량(정규화 값)은 7.25이며, 수식 (11)의 요구연산자를 적용하여 추출한 후보자원 목록은 [p4, p6, p9, p12]이다. 각 후보자원이 제공하는 서비스의 값은 p4(=14.72), p6(=13.04), p9 (=14.9) 그리고 p12(=17.01)로, 이중 최소조합인 [p4, p6]가 최종할당 되었으며 그 서비스의 총합은 27.76으로 요구서비스의 총량보다 크거나 같아야 한다는 조건을 만족하며, 또한 이 조합의 결과는 개별 서비스별로 후보 자원들의 조합이 제공하는 해당 서비스의 총합은 운용자가 요구한 해당 요구서비스의 속성값보다 크거나 같아야 한다는 조건도 만족한다.
두 번째 제한조건은 특정 자원의 최대할당 개수는 부대의 보유자원 개수보다 작거나 같아야 한다는 것으로, 시나리오상에서 동일 기능을 가진 자원의 중복을 허용하지 않기에 해당 조건도 만족한다.
세 번째 제한조건은 자원할당 시 그룹 간 자원할당을 배제한다는 것이다. 점령 시나리오에는 항구점령 그룹(yellow), 공항점령 그룹(blue) 그리고 다리폭파 그룹(green)과 같은 세 그룹이 존재하며, Fig. 7의 결과에서 특정 자원이 동일 그룹에는 다수 중복할당 되었지만 다른 그룹에는 중복할당 되지 않았음을 확인할 수 있다.
마지막 제한조건은 자원할당 시 과업-자원 간 지리적 거리정보를 반영하여 가능한 해당 과업에 근접한 자원을 할당해야 한다는 것이다. 항구점령 그룹의 과업에 할당된 자원의 개수는 총 11대로 이 중 45.5 %인 5대가 동일 그룹 내에서 중복할당 되었으며, 공항점령 그룹의 과업에 할당된 자원들은 100 % 동일 그룹 내에서 중복할당 되었음을 확인할 수 있다. 이는 그룹 내 과업들의 수행 위치가 근접하기에 발생하는 것으로, 특정 과업의 자원할당 시 자원-과업의 지리적 거리 dti를 반영하기에 해당 과업 수행 위치와 멀리 위치하는 자원보다 그룹 내 근접 과업에 기 할당된 자원이 선택될 가능성이 크기 때문이다.
5. 결 론
본 논문에서는 다중/이종 무인전투체계의 임무계획을 위한 과업-자원 할당 기법을 제안하였다. 이를 위해 임무, 과업, 서비스 그리고 자원의 계층으로 임무를 표현하는 개선된 MTSR 모델을 제안하였으며, 재정의된 MTSR 모델에 기반하여 요구연산자를 활용한 서비스들의 조합으로 과업을 식별하는 방식과 요구 서비스를 매개체로 각 과업을 수행할 자원들을 결정하는 효율적 과업-자원 할당 기법을 제시하였다. 제안한 요구서비스 기반 과업-자원 할당 기법의 성능검증을 위해 점령 시나리오를 활용한 자원 매칭 시뮬레이션을 수행하고 그 결과를 분석하였으며, 제안한 자원할당 알고리즘에서 고려되어야 할 네 가지 제한조건을 만족하는 최소조합의 자원할당이 이루어짐을 확인하였다.
후 기
이 논문은 2023년 정부의 재원으로 수행된 연구 결과임.