서 론
현대전에서 스텔스 기술은 생존성 및 효율성과 직결되는 요소이다. 스텔스 성능의 향상은 아군 전투기의 손실을 최소화하면서 적에게 큰 타격을 입힐 수 있다. 같은 임무를 수행한다고 할 때, 스텔스기로 수행하는 경우가 비 스텔스기로 수행하는 경우에 비해 작전비용이 수 십배 적게 소요된다[1]. 스텔스 기술이란 전파, 가시광선, 음파, 적외선 등 모든 관측수단에 의한 탐지를 피하는 기술을 통칭하나, 통상적으로 레이더에 의한 피탐지를 회피하는 용어로 사용된다. 스텔스 능력의 지표로는 레이더 단면적(RCS, Radar Cross Section)이 사용된다.
RCS란 레이더에 노출된 물체가 송신 신호에 반사되어 되돌아오는 수신 신호의 세기를 가상의 면적으로 나타낸 것이다[2]. RCS를 낮추기 위해 형상 최적화, 전파흡수구조(RAS, Radar Absorbing Structure), 전파흡수재료(RAM, Radar Absorbing Material) 등을 이용한 다양한 연구가 활발히 진행되고 있다[3]. RCS 특성은 해석과 측정을 이용하여 분석 할 수 있다. RCS 해석은 다양한 수치해석적 방법을 사용하여 진행한다. 정확한 해석을 위해 full-wave simulation 을 진행할 경우, 매우 긴 해석시간이 소요되고, 큰 메모리 용량과 고성능의 워크스테이션을 필요로 한다. 또한 상용 RCS 코드를 사용하더라도 수 dBsm의 오차는 불가피하기 때문에 해석으로 측정을 완전히 대체하기는 불가능하다[4].
RCS 측정 기술에는 원전계 측정시설, compact range 측정시설, 근전계 측정시설이 있다. 원전계 측정시설은 피시험체와 레이더 간의 거리가 충분히 큰 시험 시설을 의미한다. 원전계 측정을 하기 위해서는 식 (1)과 같은 원전계 조건을 만족해야 한다. 식 (1)에서 R은 레이더와 피시험체 사이의 거리, D는 피시험체의 최대 크기, λ는 파장이다[5].
원전계 측정 시설은 short pulse를 이용해 RCS를 바로 추출할 수 있다는 장점이 있지만, 안테나와 피시험체 사이의 매우 긴 거리를 요구하기 때문에, 큰 부지를 확보해야 하는 단점이 있다.
Compact range 측정시설은 반사판을 활용하여 피시험체에 입사하는 신호와 피시험체에서 반사되는 신호를 평면파로 변환한다[6]. 이 또한 RCS를 바로 추출할 수 있는 장점이 있지만, 실기체를 측정하기 위한 quiet zone을 형성하는 것이 기술적으로 어렵고 경제적으로 비효율적인 문제점이 있다[2].
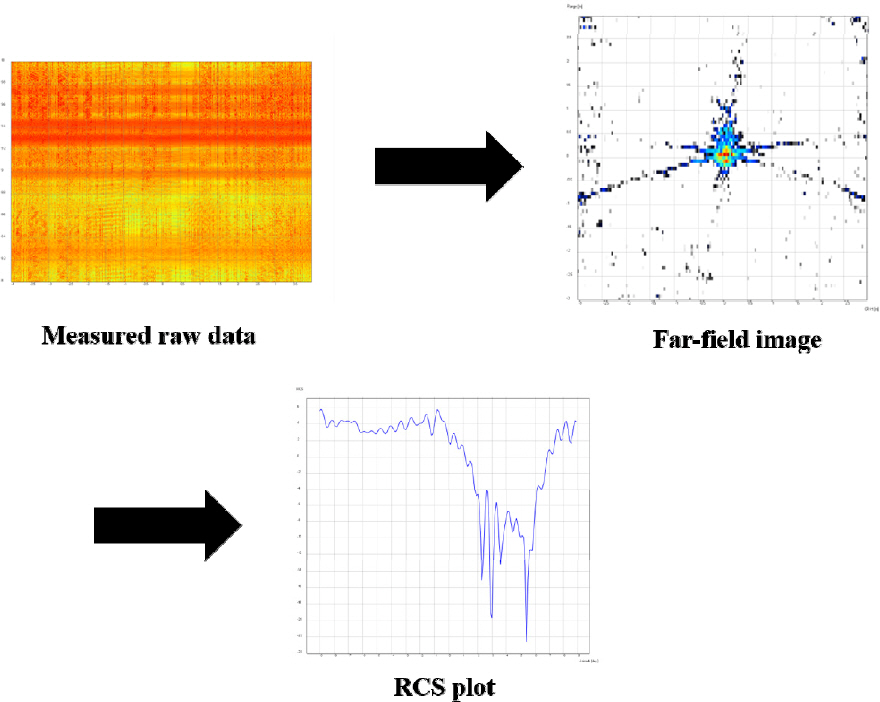
국방과학연구소 제 5시험장에서는 위와 같은 이유로 Fig. 1과 같은 실기체급 야외 근전계 RCS 측정시설을 운용중에 있다. 근전계 RCS 측정시스템은 Fig. 2와 같이 근전계에서 주파수 sweep을 통해 원시데이터를 획득하고, 근전계-원전계 변환 알고리즘을 활용하여 거리, 위상, 안테나 빔 패턴을 보상하여 원전계 레이더 이미지를 생성한다. 이미지 상 나타나는 각각의 scattered point를 바탕으로 수신안테나에서의 backscattered E-field를 역산하여 원전계 RCS를 추출한다. 이 방식은 원시데이터로부터 RCS를 추출하는 시간이 상대적으로 오래 걸리지만, 작은 부지에서도 운용이 가능하며 경제적인 장점이 있다.
시험장에서는 2차원 혹은 3차원 상의 레이더 이미지를 얻기 위해 2D ISAR(Inverse Synthetic Aperture Radar), 2D SAR(Synthetic Aperture Radar) 혹은 3D cylindrical 측정을 수행한다. 2D ISAR 측정은 턴테이블을 방위각 방향으로 회전시켜 주파수와 방위각에 대한 데이터를 획득하고, 2D SAR 측정은 안테나를 지면에 수직인 방향으로 이동시켜 주파수와 안테나 높이에 따른 데이터를 획득하며, 3D cylindrical 측정은 안테나 높이를 바꾸며 턴테이블을 회전시켜 주파수, 방위각, 안테나 높이에 따른 데이터를 획득한다.
레이더 이미지를 얻어서 RCS를 추출하는 근전계 RCS 시스템의 특성상, RCS 계산을 위한 원시데이터를 측정하는데 시간이 오래 걸리는 어려움이 있다. 이 때문에 주어진 시험기간 안에 많은 형상에 대한 시험을 진행하는데 제약이 있다. 특히 tripod support 의 영향성을 정확하게 제거하고, 야외 시험장의 환경에서 생기는 클러터를 효과적으로 제거하기 위한 3D cylindrical 측정의 경우, 2D ISAR 측정에 비해 30 배의 시간이 더 소요된다.
본 논문에서는 항공기 형상에 대한 2D ISAR 측정 데이터의 방위각 영역에서 내삽 알고리즘을 적용한 결과와 통상적으로 측정한 결과를 비교하여 내삽 알고리즘의 효과와 한계에 대하여 분석하였다.
근전계 RCS 측정시스템에서의 수식
2.1 원전계 RCS 추출 알고리즘
송신안테나에서는 수직 혹은 수평 편파의 전파를 SFCW(Stepped Frequency Continuous Wave) 레이더와 같이 송신하여 주파수 sweep을 진행하고, 수신안테나에서는 송신안테나와 동일한 편파의 신호를 수신한다. Fig. 3과 같이 송수신안테나는 지면과 수직인 안테나 타워를 따라 같이 움직이고 타겟과 안테나 사이의 고각은 θ로 나타난다. 턴테이블의 회전에 따른 방위각은 ϕ로 나타난다. 타겟을 각각의 독립된 등방성의 산란점으로 가정한다면, reflectivity 분포를 s(r)로 나타 낼 수 있다. 수신안테나에서 수신되는 근거리 장 전계 u는 안테나의 위치와 주파수의 함수이고, 식 (2)와 같이 나타낼 수 있다. 식 (2)에서 ra는 안테나의 위치벡터이고, f는 주파수, k는 파수, G는 안테나 이득, V는 타겟이 차지하는 공간상의 부피이다[7].
모든 안테나 측정위치와, 대역폭에 대해서 수신안테나에 되돌아오는 전계 u를 측정하면, 식 (3)을 이용하여 s(r)을 역산할 수 있다. 식 (3)에서 B는 주파수 대역폭이다[7].
식 (3)에서 얻은 s(r)은 원전계 레이더 이미지 상에서 픽셀로 나타나고, 그 값이 클수록 산란점의 reflectivity가 크다. 식 (3)에서 ej2k|r-ra|항은 구면파와 평면파의 위상을 보정하고, G2(θ,ϕ,f)은 안테나의 빔 패턴을 보상하고, |r-ra|2은 거리에 따른 세기의 손실을 보상한다. 식 (3)을 통해 얻은 원전계 레이더 이미지 s(r)을 바탕으로 식 (4), (5)를 이용하면 수신안테나의 특정 위치에서 계산되는 원전계 RCS 값을 얻을 수 있다. p ^
2.2 2D ISAR 측정 시 파라미터 설정
ISAR 측정을 하기 전에 Radio Frequency(RF) 파라미터와 방위각 파라미터를 설정한다. RF 파라미터는 안테나의 높이, 피시험체 크기 등 시험 환경에 맞게 레이더 이미지의 range 해상도와 range extension을 고려하여 결정한다. range 해상도와 extension은 식 (6), (7)과 같이 나타낼 수 있다. ρR은 range 해상도, c는 빛의 속도, fmax는 측정하는 최대 주파수, fmin는 측정하는 최소 주파수, θ는 측정하는 각도 측정범위, △R은 range extension,Nf은 주파수 영역에서 측정하는 샘플 개수이다[7].
피시험체의 크기가 크거나, 안테나로부터 피시험체보다 멀리 떨어진 클러터가 영향을 미치는 경우, 대역폭을 줄이거나, 같은 대역폭 내에서 샘플의 개수를 늘려야 한다. 하지만 대역폭을 줄이게 되면 거리방향의 해상도가 낮아지는 문제점이 발생한다. 샘플의 개수는 ISAR 측정 시, 턴테이블의 최소 회전속도에 의해 제한된다. sweep time이 길어지면 데이터의 손실이 발생할 수도 있기 때문이다. 시험장에서 진행하는 RCS 시험에서는 대다수의 경우 하드웨어 gating을 이용하여 환경 클러터를 제거하여, range extension의 한계를 극복하고 있다.
방위각 파라미터는 레이더 이미지의 cross range(CR) 해상도와 CR extension을 고려하여 파라미터를 설정한다. CR 해상도와 extension은 식 (8), (9)과 같이 나타낼 수 있다. ρCR은 CR 해상도, c는 빛의 속도, fmax 는 측정하는 최대 주파수, θ는 측정하는 각도 측정범위, △CR은 CR extension, NCR은 방위각 영역에서 측정하는 샘플 개수이다[7].
CR 해상도는 일반적으로 측정하고자 하는 방위각 범위에 의해 정해지나 CR extension은 야외 환경 클러터의 aliasing을 방지하기 위해 통상적으로 피시험체 길이의 2 ~ 3배로 설정한다. extension을 크게 하기 위해서 방위각 샘플 개수를 늘리면 측정시간이 증가하는 문제점이 있다. 또한 방위각 샘플 개수를 늘리는 것은 턴테이블의 최소 회전속도에 의해 한계가 결정된다. 측정 시 CR extension을 적절히 유지하면서 샘플 개수를 줄이는 것이 중요하다.
내삽 알고리즘의 적용에 따른 결과
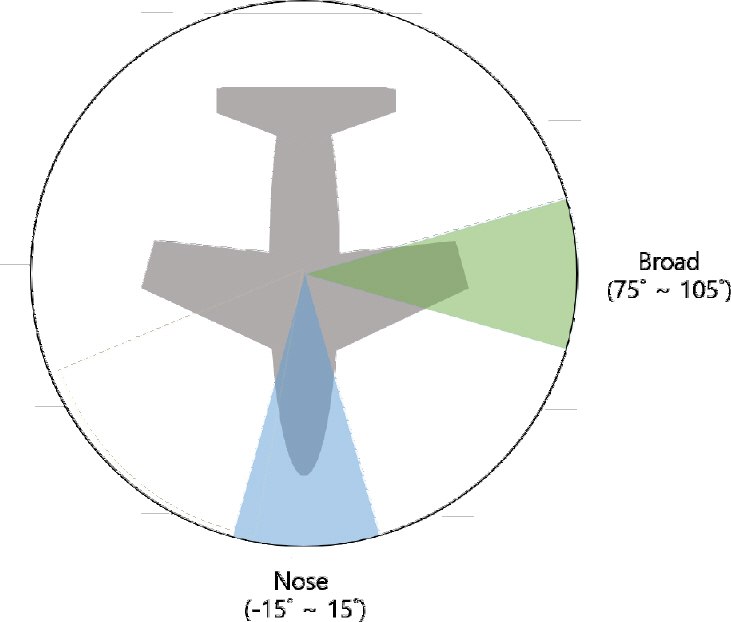
타겟과 레이더 와의 거리는 200 m이고, 항공기 형상의 타겟은 턴테이블 상에 있는 tripod support에 설치되었다. 중심 주파수 10 GHz, 대역폭 2 GHz(9 ~ 11 GHz, 1401 샘플 수)로 측정하였고, Fig. 4와 같이 전체적으로 RCS 레벨이 고르게 측정되는 nose 섹터(방위각 -15 ° ~ 15 °, 865 샘플 수)와 방위각 90 ° 근방에서 피크가 존재하는 broad 섹터(방위각 75 ° ~ 105 °, 865 샘플 수)에 대해서 2D ISAR 측정하였다.
측정된 데이터는 주파수, 방위각에 따라 수신된 전계의 크기와 위상의 값이며, 1401×865의 복소수 데이터이다. 본 논문에서는 원 데이터를 무손실 데이터라고 명명하고, 무손실 데이터 대비 샘플링된 데이터의 비율을 샘플링 비율로 나타내었다.
샘플링 비율에 따라 원전계 RCS를 추출하여 무손실 데이터에서 계산한 원전계 RCS와의 차이를 비교하였고, 샘플링 데이터에 내삽 알고리즘을 적용하였을 때 그 차이가 얼마나 줄어들었는지 나타내었다. 본 논문에서는 샘플링 데이터를 전체 방위각 데이터에서 동일한 간격으로 n개 중 m개의 샘플링을 통해 획득하였다. 이 때, n은 샘플링 주기를 의미하여, m은 샘플링 주기에서 선택되는 데이터 수를 의미한다.
내삽이란 어떤 두 점의 값이 주어졌을 때, 그 사이에 위치한 값을 추정하는 방법이다[8]. 본 논문에서는 방위각 영역에서 가장 근접한 두 측정데이터를 이용하 여 내삽 알고리즘을 적용하였다. 샘플링 비율이 50 % 이상인 조건에서는 Fig. 5 (a)와 같이 최근접 두 데이터의 평균을 통해 계산하였고, 샘플링 비율이 50 % 미만인 조건에서는 Fig. 5 (b)와 같이 최근접 두 데이터에서 떨어진 거리에 따라 선형적으로 계산하는 내삽법을 이용하였다.
Nose 섹터에 대한 내삽 알고리즘 적용 결과
Fig. 6에서는 샘플링 된 데이터를 바탕으로 계산된 원전계 RCS 데이터와 무손실데이터간의 평균제곱근편차(RMSE) 값과 샘플링 된 데이터에 내삽 알고리즘을 적용한 뒤 계산한 원전계 RCS 데이터와 무손실데이터간의 RMSE값을 샘플링 비율에 따라 비교하여 나타내었다. 각 RMSE 값은 linear에서 계산한 후 dBsm 단위로 변경하였다.
샘플링 비율이 낮아질수록 무손실 데이터와의 RCS 차이가 크게 나타나지만, 내삽 알고리즘을 적용하면 그 차이를 대폭 완화할 수 있음을 보여준다. 내삽 알고리즘을 적용하지 않으면 모든 sampling rate에서 -4 dBsm 이상의 RMS 오차를 나타내는 반면, 내삽 알고리즘 적용 시, sampling rate 30 % 이하에서만 -4 dBsm 이상의 차이를 보인다. 또한 내삽을 적용하지 않은 데이터는 샘플링 비율이 작아짐에 따라 무손실데이터와 급격한 차이를 보이지만, 내삽을 적용한 데이터는 샘플링 비율에 따라 큰 차이를 보이지 않는다.
Fig. 6.
Comparison of the Root Mean Square Error (RMSE) value between the data with interpolation and the data without interpolation according to the sampling rate in nose sector
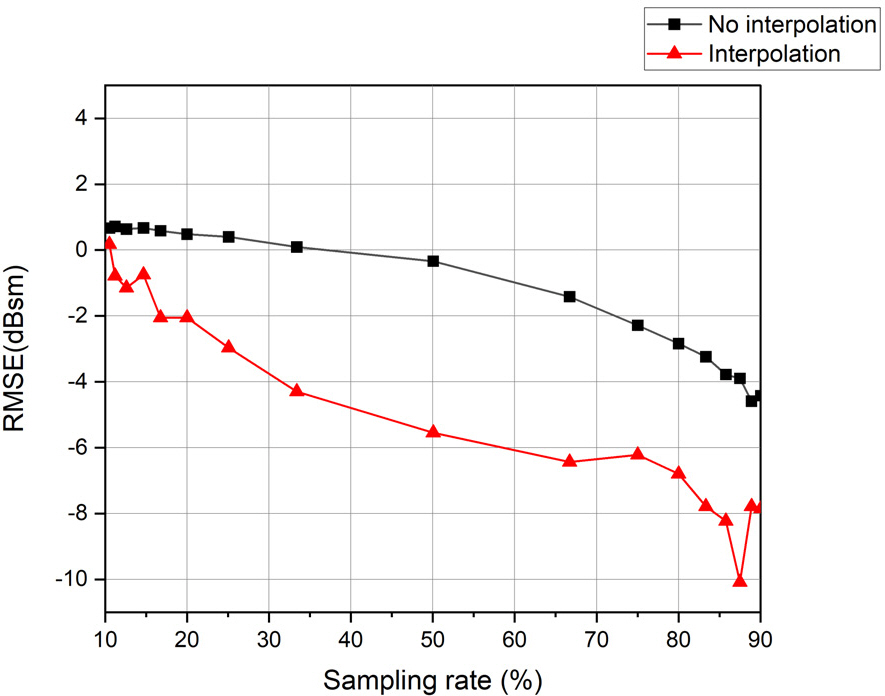
Fig. 7.
Comparison of the RCS value in azimuth angle between lossless data, the data with interpolation and the data without interpolation according to the sampling rate in nose sector
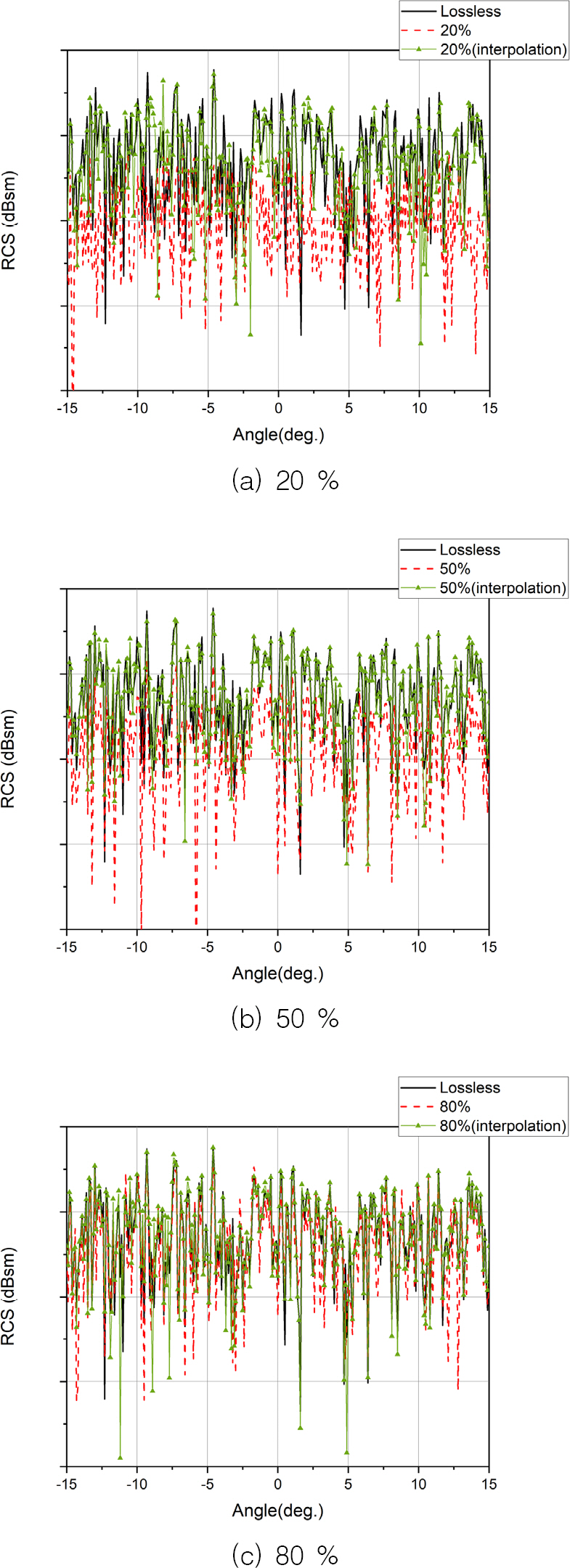
Fig. 7에서는 샘플링 비율에 따라 무손실 데이터와 내삽 알고리즘을 적용하지 않은 데이터, 내삽 알고리즘을 적용한 데이터를 방위각에 따라 RCS를 나타내었다. Fig. 7 (a)를 보면 내삽 알고리즘을 적용한 결과는 샘플링 비율이 20 % 일 때에도 비교적 무손실 데이터를 잘 추종하는 것을 알 수 있다. 하지만, Fig. 7 (c)를 보면 내삽 알고리즘 미적용한 결과는 샘플링 비율이 80 % 일 때에도 무손실 데이터와 차이가 나는 것을 알 수 있다.
Broad 섹터에 대한 내삽 알고리즘 적용 결과
Nose 섹터와 마찬가지로, Fig. 8에서 샘플링 된 데이터를 바탕으로 계산된 원전계 RCS 데이터의 RMSE 값과, 샘플링 된 데이터에 내삽 알고리즘을 적용한 뒤 계산한 원전계 RCS 데이터의 RMSE를 샘플링 비율에 따라 비교하였다.
Fig. 8.
Comparison of the Root Mean Square Error (RMSE) value between the data with interpolation and the data without interpolation according to the sampling rate in broad sector

Broad 섹터에서도 내삽 알고리즘을 이용하여 무손실데이터와의 차이를 완화할 수 있음을 알 수 있다.
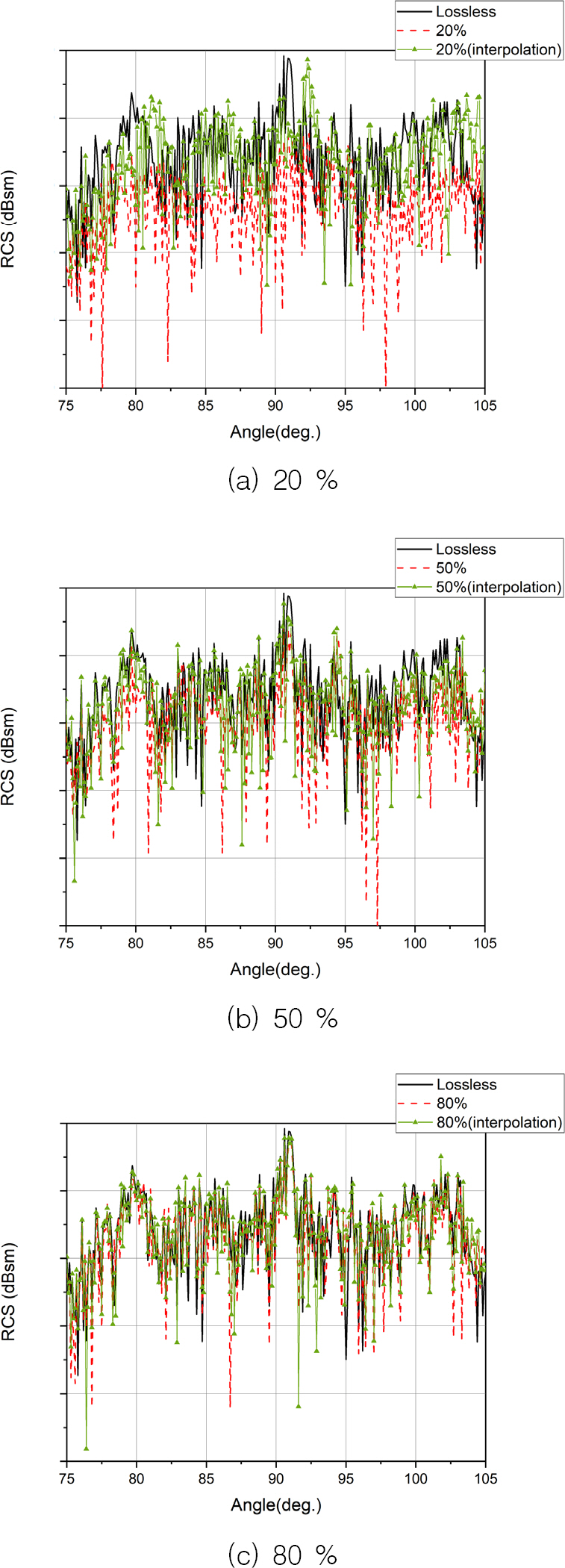
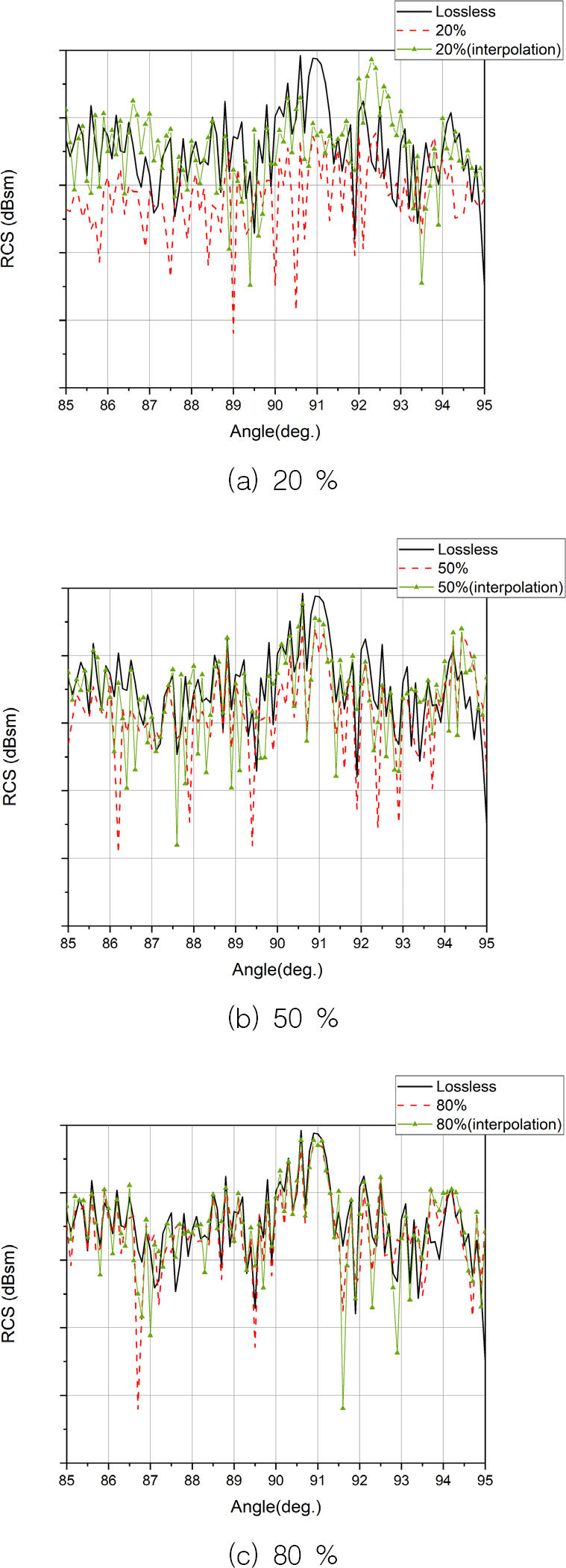
Fig. 9에서는 샘플링 비율에 따라 무손실 데이터와 내삽 알고리즘을 적용하지 않은 데이터, 내삽 알고리즘을 적용한 데이터를 방위각에 따라 RCS를 나타내었다. 타겟의 90 ° 근방에서 나타나는 피크는 타겟 설치 시 발생하는 오차로 인해 일반적으로 1 ~ 2 ° 이동 하여 나타난다. Fig. 9(a)와 같이 샘플링 비율이 20 % 일 때에는 전체적인 경향도 일치하지 않을뿐만 아니라, 피크값도 다르고, 피크의 방위각 위치가 다르게 나타나는 문제점이 생긴다. Fig. 9 (c)를 보면, 샘플링 비율 80 % 일 때에는 무손실 데이터와 전체적으로 경향성은 유사하지만, nose에 비해 부정확한 것을 알 수 있다. 또한 Fig. 9 중 방위각 85 ~ 95 °를 추출하여 나타낸 Fig. 10을 보면, Fig. 10 (c)에서와 같이 샘플링 비율이 80 % 일 때조차 내삽 알고리즘을 적용한 결과의 피크값이 정확하지 않음을 알 수 있다.
결 론
본 논문에서는 야외 RCS 근전계 측정시스템에서 발생하는 긴 측정시간의 문제점을 극복하기 위하여 내삽 알고리즘을 제안하였다. 야외 200 m range에서 항공기 형상에 대해 ISAR 측정한 데이터를 바탕으로 비교적 균일하게 RCS 값이 존재하는 nose 섹터와 방위각 90 ° 근방에서 피크가 존재하는 broad 섹터에 대하여 내삽 알고리즘을 적용한 결과를 비교하였다. 각 경우 모두, 내삽 알고리즘을 적용한 결과가 적용하지 않은 결과보다 무손실 데이터의 RCS 결과와 유사함을 알 수 있었다.
Broad 섹터에서 샘플링 비율이 낮아질 때 RCS 평균값은 작게 나타났지만, 실제로 방위각에 따른 RCS 값을 비교한 결과에는 피크값과 피크가 생성되는 방위각 위치가 부정확하게 나타난 것을 알 수 있었다. nose 섹터에서는 샘플링 비율이 낮을 때에도 방위각에 따른 RCS 값이 무손실 데이터와 매우 유사하게 나와서 피크가 없는 섹터가 내삽 알고리즘을 적용하기에 적합함을 보였다.
피시험체의 방위각에 따른 RCS 특성을 미리 확인하여, 피크값 주위의 방위각은 기존 방법대로 샘플 수를 늘려 측정하고, 피크가 없는 섹터는 샘플 수를 줄이고 내삽알고리즘을 적용하면 이와 같은 문제점을 해결할 수 있을 것으로 생각된다.
본 논문에서 제안하는 내삽 알고리즘을 활용하면 CR extension을 기존 측정 방법대로 확보하면서도, 데이터 측정시간을 획기적으로 줄일 수 있다. 향후 RCS 측정 시 측정시간을 단축함으로써 다방면으로 효율적인 시험을 진행할 수 있을 것으로 예상된다.