시뮬레이션을 통한 레이저 융삭 추진의 우주 쓰레기 제거 응용 가능성 연구
Research on Applicability of Laser Ablation Propulsion to Space Debris Removal by Simulations
Article information
Trans Abstract
Laser ablation propulsion(LAP) is the method to create impulse by laser ablation. It can be used to deorbit the space debris(SD), as its long-range property and versatility on any material. In this paper, we find out several requirements of the LAP system(LAPS) to deorbit the SD by simple numerical calculations of the SD orbit and laser beam flux. As a result, minimum operable altitude angle turned out to be a crucial variable to the LAPS. Moreover, if minimum operable altitude angle is 10°, and if the minimum distance between the LAPS and the SD is below 450 km, 1 m/s2 is sufficient to deorbit the SD by once. With 18 kJ/3 ns pulsed laser and cube shaped 100 kg SD, 1 m/s2 acceleration can be achieved by increasing the pulse repetition rate over 34~53 Hz, depending on the size of the SD. This capability could compare with the conceptual design of the Japan Establishment for a Power-laser Community Harvest(J-EPoCH) facility, which include 8 kJ, 5 PW@100 Hz laser.
기 호 설 명
W: 레이저 펄스의 순간 Power 벡터
Φ: 레이저 펄스의 순간 Power 면밀도 벡터
r0: LAPS의 위치 벡터
r: SD의 위치 벡터
rmin: SD 궤도의 근지점과 지구 중심 사이 거리
m: SD의 질량
v: SD의 속도 벡터
E: SD의 역학적 에너지
L: SD의 궤도 각운동량 벡터
ε: SD의 궤도 이심률 벡터
F: SD가 받는 힘 벡터
τ: SD가 받는 토크 벡터
1. 서 론
현대 사회에서 우주 영역은 대체 불가능한 자원으로 급부상하였다. 그로 인해 우주 탐사 및 개발에 참여하는 국가는 점차 많아지고 있으며, 이에 의한 우주 쓰레기(SD)도 급격히 증가하고 있다. 이러한 SD의 과격한 급증이 이어지면 인공위성의 연쇄 추돌에 의한 Kessler syndrome을 유발하며[1], 각국의 우주 안보에도 상당한 악영향을 미치게 된다. 따라서 우주 전력 유지를 위해 SD를 제거하기 위한 연구가 필요하다. 이에 본 논문에서는 SD를 제거하는 방법의 하나로 레이저 융삭 추진(LAP)을 시도하였다.
LAP는 펄스 레이저를 물체에 조사하여 융삭된 물체 표면에 의해 생기는 추력을 추진으로 사용하는 방법이다. 이 방법은 추진체와 레이저 발진기 사이의 거리에 제한이 없으므로 in-space propulsion으로써의 활용에 대한 논의가 지속해서 이루어지고 있다[2]. 또한, 융삭 현상은 모든 고체 물질에서 일어나는 현상이므로 추진체의 연료가 필요 없다. 따라서 레이저 융삭 추진은 통제 능력을 상실한 SD를 제거하기 위한 용도로 사용될 수 있다[3].
따라서 본 논문에서는 시뮬레이션을 통해 지상에 배치된 LAP 시스템(LAPS)을 운용하여 SD를 대기권으로 재진입하는 데 필요한 LAPS의 요건을 구하고자 한다.
2. 기반 이론
2.1 레이저 융삭에 의한 추력 효율
빛의 추력 효율 cm은 빛의 Power에 따른 물체의 추력 비율을 뜻한다. 이를 다음 식으로 정의할 수 있다[2].
빛이 물체에 단순히 반사할 때에도 빛의 운동량 변화가 있으므로 복사압이 발생한다. 빛의 운동량과 에너지는 각각 h/λ와 hf이므로, 빛이 물체의 표면에 수직으로 들어와서 정반대로 반사되는 경우 cm은 다 음과 같이 된다.
이때 h는 플랑크 상수, λ는 빛의 파장, f는 빛의 주파수, c는 빛의 속도다. 따라서 이 경우 1 GW의 빛으로 약 6.67 N의 힘을 가할 수 있다.
반면, LAP는 물체의 표면을 추진체로 사용하기 때문에 복사압보다 훨씬 더 높은 cm을 보여준다. Fig. 1은 C. Phipps et al.(2012)에서 분해 폭발을 일으키지 않는 물질을 대상으로 cm을 측정한 실험 결과들의 fitting model[2]을 보여준다. Fig. 1에 의하면 cm은 레이저 펄스의 Φ, λ, 그리고 펄스 지속 시간에 따라 100 N/MW 도 넘을 수 있다.
2.2 LAPS에 의한 SD의 궤도 수정
지구 주위를 돌고 있는 모든 SD의 궤도는 다음 식을 만족한다.
이때 k=GMm이며, G는 중력 상수, M은 지구 질량이다. 이심률 벡터 ε는 다음과 같다.
또한, SD의 위치가
근지점은 지구 대기와 가장 가까워지는 지점이므로 SD의 대기권 재진입에 가장 민감한 변수다. 따라서 LAPS를 이용하여 SD를 대기권으로 재진입하기 위해서는 rmin가 낮아지도록 LAPS를 작동하면 된다. 이를 식으로 표현하면 다음과 같다.
레이저 펄스에 의해 SD의 속도가 δv 만큼 바뀌면 이에 의해 rmin도 δrmin만큼 바뀐다. δrmin를 전개하면 다음과 같다.
이때 이심률 크기의 변화 δε는 다음과 같다.
식 (8)을 식 (7)에 대입하면 다음과 같다.
또한 E의 변화 δE와 L2의 변화 δL2는 다음과 같다.
원궤도의 경우 rmin=L2/(mk)이므로 δrmin은 다음과 같다.
따라서 식 (8), (10), (11)을 사용하면 δrmin를 r, v, δv에 대한 함수로 나타낼 수 있다. 여기서 δv 는 곧 LAPS에 의해 SD가 받는 힘에 대응된다. 또한, SD가 받는 힘의 방향은 평균적으로 LAPS에서 SD를 바라보는 Line of Sight의 방향과 같다. 이를 식으로 표현하면 다음과 같다.
2.3 SD 표면의 형태에 따라 받는 힘과 토크
레이저 펄스에 의해 미소 면적 dA가 받는 힘 dF가 다음을 만족한다고 가정하자.
이때 dS는 SD 표면의 미소 면적 벡터이다. 즉, 이 경우, 레이저 펄스에 의한 힘이 항상 표면과 수직이다. 이 가정을 만족할 때 임의의 형태를 가진 SD가 LAPS 에 의한 힘과 토크는 다음과 같다.
이때 표면이 받는 힘은 표면이 받는 레이저 펄스의 순간 power 면밀도인 Φ∙n 에 따라 변하므로 추력 효율 cm은 Φ∙n 에 따른 함수이다. 또한, rs는 dS의 위치 벡터, n 은 dS의 법선 벡터, S는 레이저 펄스에 닿은 SD의 표면 영역이다.
3. LAPS에 따른 SD 궤도의 근지점 변화
3.1 SD가 받는 가속도와 LAPS의 최소 작동 고각이 SD 궤도의 근지점에 미치는 영향
SD가 북극점에서 북위 37도의 LAPS 바로 위를 지나치는 원궤도를 돌고 있다고 가정하자. SD의 고도는 각각 Starlink 인공위성의 세 번째 껍질의 궤도인 340 km, Starlink 인공위성의 첫 번째 껍질의 궤도인 550 km[4], IridiumNext 인공위성의 고도[5]이자 가장 높은 SD 개수 밀도를 가지고 있는[6] 780 km로 정하였다. 또한, 편의를 위해 LAPS에 의해 SD가 받는 가속도를 a, LAPS 의 최소 작동 고각을 θmin이라고 한다.
LAPS는 SD의 고각이 θmin보다 높으면서, SD의 속도와 위치가 식 (6)을 만족하면 SD에 레이저 펄스를 조사한다. 이때 a의 방향은 식 (13)에서처럼 LAPS에서 SD를 바라보는 Line of Sight의 방향과 같으며, a의 세기는 항상 일정하다고 가정하였다.
계산은 SD가 북극에서 출발하여서 LAPS의 작동 가능 범위를 벗어날 때까지 행한다. 계산이 끝난 후 총 근지점 변화 △rmin을 기록하여서 LAPS에 의한 a와 θmin에 따른 △rmin의 추이를 알아본다. 만약 rmin이 80 km 아래로 떨어지면 SD는 궤도 유지가 불가능하며, 대기권으로 재진입한다[7]. 따라서 LAPS에 의해 rmin이 고도 80 km 아래로 떨어지면 SD가 확실히 지구 대기권으로 재진입했다고 판단한다.
LAPS에 의한 영향을 분명히 하기 위해 지구의 자전 이외에 공기 저항, 달과 태양에 의한 조력, 지구 중력의 higher order terms 등은 고려하지 않았으며, 수치해석 방법은 Runge-Kutta 방법(RK4)을 사용하였고, step size는 0.1 s로 하였다.
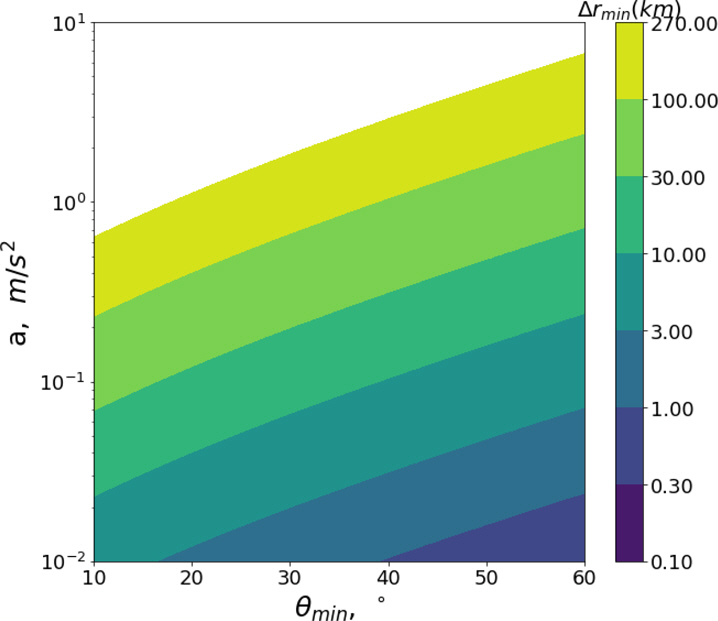
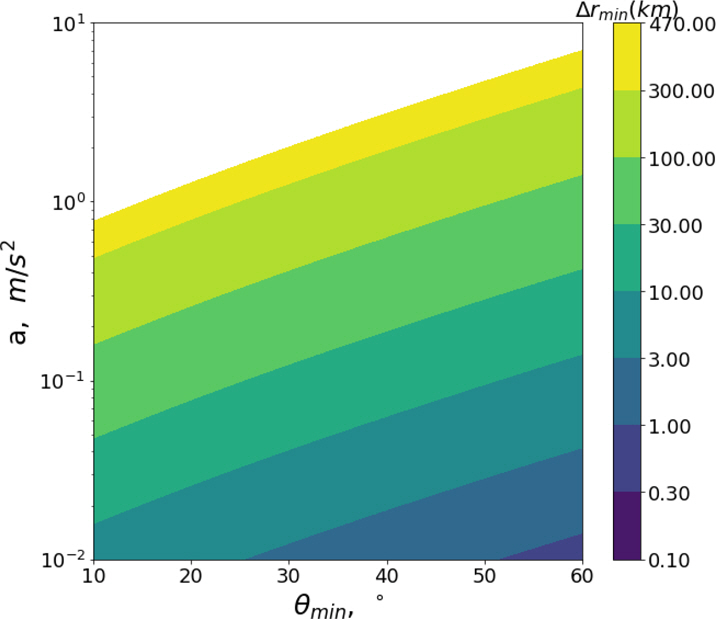
Fig. 2~4는 고도가 각각 340 km, 550 km, 780 km일 때 a와 θmin에 따른 △rmin에 대한 결과이다. 시뮬레이션 결과 a와 △rmin은 서로 선형적인 관계를 보였지만, θmin과 △rmin은 주어진 범위에 대해 지수적 관계에 근접하였다. 이는 곧 θmin이 LAPS의 성능과 직결되는 요소임을 보여준다.
또한, SD의 대기권 재진입을 위해서는 SD의 고도와 관계없이 rmin을 80 km로 낮춰야 하므로 높은 고도일수록 SD의 대기권 재진입에 필요한 △rmin도 커졌다. 그러나, SD의 고도가 높을수록 SD가 LAPS의 작동 가능 범위 내를 지나치는 시간이 증가하였으므로 △rmin 도 증가하였다. 따라서, SD의 대기권 재진입을 위해 필요한 a는 고도에 따라 크게 변하지 않는 단조 관계의 모습을 보였다.
θmin이 10°인 경우 a가 1 m/s2면 SD가 LAPS를 한번 지나치는 것만으로도 SD를 대기권으로 재진입시킬 수 있으나, θmin이 60°인 경우 a가 10 m/s2 이상 되어야 같은 효과를 받을 수 있다.
3.2 LAPS와 SD 사이 거리와 LAPS의 최소 작동 고각이 SD 궤도의 근지점에 미치는 영향
SD가 북극점에서 출발하여 북위 37도의 LAPS와 20도 이내의 경도 차로 지나치는 원궤도를 돌고 있다고 가정하자. LAPS는 SD의 고각이 θmin보다 높으면서, SD의 속도와 위치가 식 (6)을 만족하면 LAPS가 SD에 레이저 펄스를 조사한다. SD의 궤도와 LAPS의 경도 차를 θlongitude라고, LAPS가 작동하지 않을 때 SD와 LAPS 사이의 지표면 상 최소 거리를 dmin이라고 할 때, θlongitude과 dmin은 근사적으로 다음과 같은 관계를 가지고 있다.
구분을 위해 SD가 LAPS의 서쪽 지점으로 진입하면 dmin을 음수로 표시하였으며, 동쪽 지점으로 진입하면 dmin을 양수로 표시하였다.
수치해석 방법은 RK4를 사용하였으며, step size는 0.1 s로 하였다. LAPS를 한 번 지나친 후 총 근지점 변화 △rmin을 기록하여서 dmin와 θmin에 따른 △rmin의 추이를 통해 LAPS가 어느 정도 거리까지 영향을 줄 수 있는지 알아보았다. 또한, a는 1 m/s2로 고정해서 이때 LAPS의 사거리를 구하고자 하였다.
Fig. 5~7은 고도가 각각 340 km, 550 km, 780 km일 때 a와 θmin에 따른 △rmin에 대한 결과이다. Fig. 5~7에서 바깥쪽 흰색 부분은 SD가 LAPS의 작동 가능 범위에 들어오지 않아서 근지점 고도의 변화가 없었던 부분이다. 고고도에 있는 SD는 더욱 먼 거리에서도 LAPS의 영향을 받을 수 있음을 알 수 있다. 또한, 안쪽 흰색 부분은 rmin이 80 km보다 낮아져서 대기권으로 재진입한 부분이다.
인공위성의 고도가 높을수록 LAPS가 SD를 대기권으로 재진입시킬 수 있는 거리가 약간씩 줄어들었으나, θmin가 10°일 때 dmin이 450 km 내에 있으면 고려한 모든 고도에 대해 SD를 떨어트릴 수 있었다. 또한, LAPS의 동쪽으로 진입한 SD보다도 서쪽으로 진입한 SD의 rmin이 LAPS에 의해 더욱 떨어지는 모습을 보였다. 이는 계산에서 지구의 자전이 고려되었기 때문이며, SD가 LAPS로 접근하는 시점에서 rmin이 낮춰진다는 사실을 보여준다.
4. 레이저 펄스에 의해 정육면체가 받는 운동량, 각운동량 변화
SD에 특정 가속도를 가하는 데 필요한 레이저의 성능을 구하기 위해 A. Rubenchik et al.(2018)에서 제시된 레이저 펄스[8]를 정육면체 SD에 조사하는 시뮬레이션을 진행하였다. 레이저 펄스의 사양은 λ = 1 µm, 펄스 지속 시간 t = 3 ns, 순간 출력 W = 6 TW, 빔 반지름 rf = 34 cm, 빔 품질 M2 = 2이다. 레이저 펄스의 형태는 top-hat shape이며, 지속 시간 내에서 균일하다고 가정하였다.
레이저 펄스에 의한 SD의 운동량 변화와 각운동량 변화를 계산하기 위해, 먼저 레이저 펄스의 출력 flux 를 여러 개의 미소 성분으로 나누어서 각 성분이 정육면체에 닿는 지점과 그에 따른 Φ∙n 을 계산하였다. 그 후, 각 미소 성분에 대해 식 (15), (16)을 적용하면 SD의 운동량 변화와 각운동량 변화를 계산할 수 있다.
본 절에서는 레이저 펄스가 진입하는 방향의 방위각과 고각에 따른 SD의 운동량 변화와 각운동량 변화를 계산하였다. SD는 모서리 길이 0.5 m ~ 2 m의 정육면체이며, 레이저 펄스는 언제나 SD의 중심을 향해 들어온다. 정육면체의 중앙이 원점이고 축이 모든 면에 대해 수직일 때 각 팔분공간에 대한 대칭이 있으므로 레이저 펄스가 SD로 들어오는 방향의 방위각과 고각은 각각 0°에서 90°까지만 고려하였다.
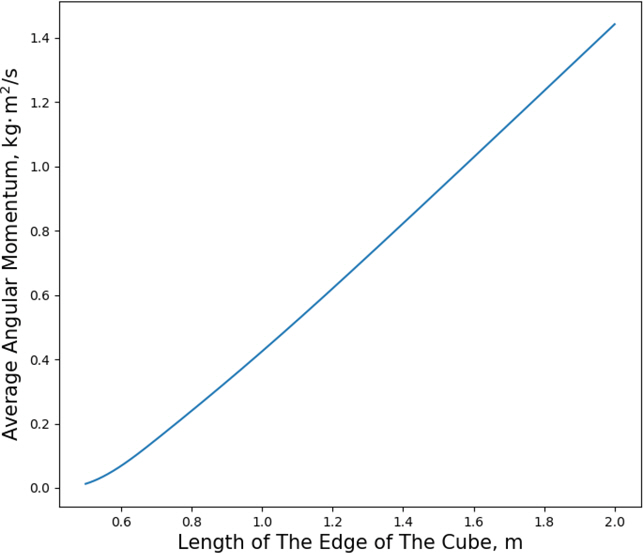
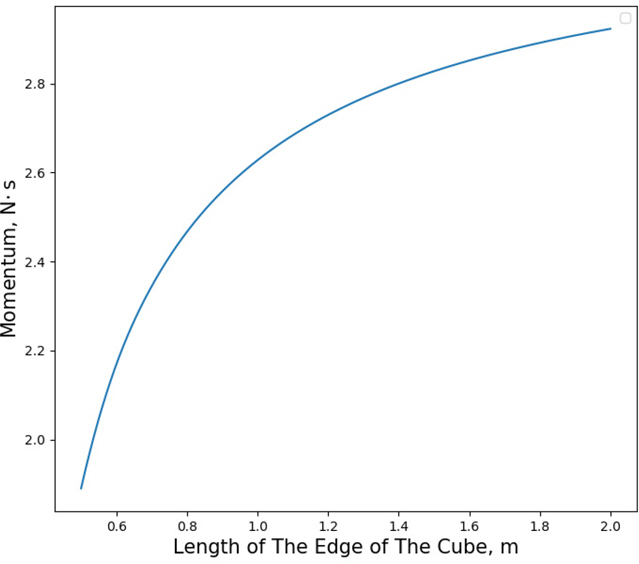
Fig. 8~13은 모서리의 길이가 0.5 m, 1 m, 2 m일 때 레이저 펄스의 입사각에 따라 정육면체가 받는 운동량과 각운동량 분포를 나타내며, Fig. 14, 15는 정육면체의 모서리 길이에 따라 정육면체가 받는 평균 운동량 변화와 각운동량 변화를 나타낸다. Fig. 8~13에서 검은 선은 정육면체의 모서리를 나타낸다.
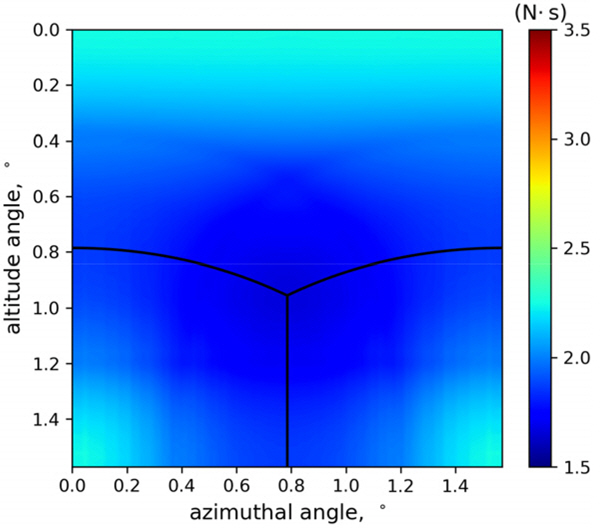
Momentum difference by the laser pulse with respect to altitude angle and azimuthal angle when the length of the edge of the cube is 0.5 m
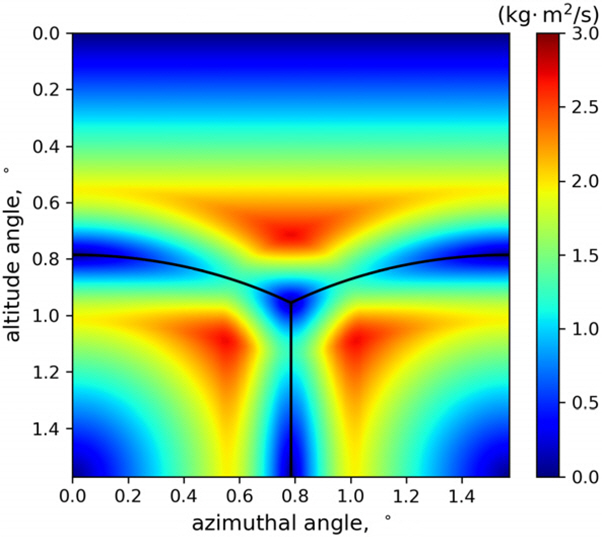
Angular momentum difference by the laser pulse with respect to altitude angle and azimuthal angle when the length of the edge of the cube is 2 m
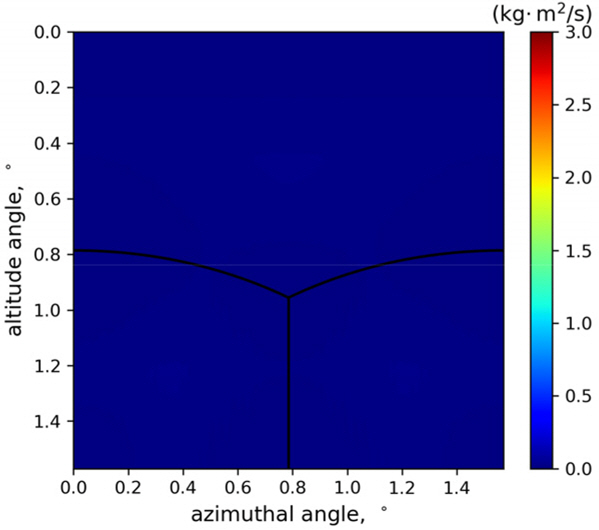
Angular momentum difference by the laser pulse with respect to altitude angle and azimuthal angle when the length of the edge of the cube is 0.5 m
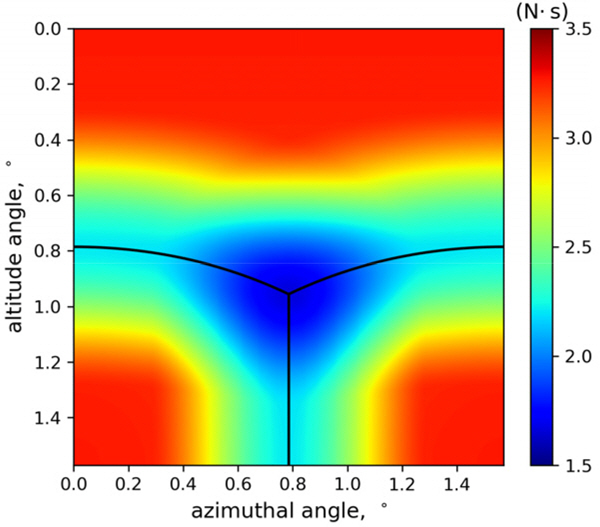
Momentum difference by the laser pulse with respect to altitude angle and azimuthal angle when the length of the edge of the cube is 1 m

Angular momentum difference by the laser pulse with respect to altitude angle and azimuthal angle when the length of the edge of the cube is 1 m
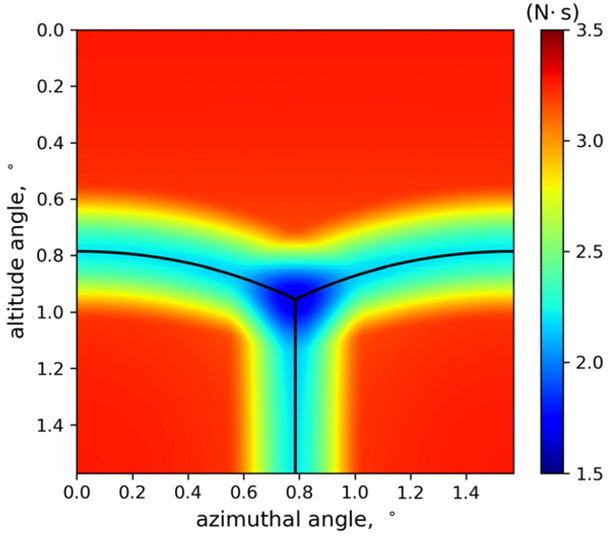
Momentum difference by the laser pulse with respect to altitude angle and azimuthal angle when the length of the edge of the cube is 2 m
계산 결과 정육면체의 모서리 길이에 따라 평균 1.9~2.9 N・ s의 운동량 변화와 0~1.4 kg・ m2/s의 각운동량 변화가 나타났다. 그리고 레이저 펄스가 모서리나 꼭짓점에 도달할 때 둘 이상의 면에 의해 힘을 받아서 서로 상쇄되는 모습을 보였다. 따라서 SD의 표면에 굴곡이 없을수록 레이저 펄스에 의한 힘이 분산되지 않아서 더욱 높은 추력을 낼 수 있음을 알 수 있다.
위 결과를 토대로 만약 SD의 질량이 100 kg이라면, SD에게 1 m/s2의 가속도를 주기 위해서는 약 34~53 Hz 의 반복 빈도가 필요함을 알 수 있다. 이는 Japan Establishment for a Power-laser Community Harvest (J-EPoCH)의 개념적 설계에 포함된 8 kJ, 5 PW@100 Hz 펄스 레이저[9], 그리고 P. Mason et al.(2011)에서 1 kJ/~ns@ 10 Hz diode-pumped solid state laser의 최적화된 설계[10]에 버금가는 성능이다.
그뿐만 아니라 약 1520.95 kg・ m2의 관성 모멘트를 가진 태양동기궤도 위성이 태양 지향 자세에서 한 궤도당 3 kg・ m2/s의 외란 각운동량을 받는다는[11] 사실을 SD의 평균 각운동량 변화와 비교해보면 LAPS는 SD에 강한 회전을 가한다는 사실을 알 수 있다. 이는 LAPS가 SD를 회전시켜서 평균적으로 식 (13)을 만족하게 됨을 뜻한다.
5. 결 론
수치해석 기법들을 활용한 여러 궤도 계산을 통해 LAPS에 의한 SD 궤도의 근지점 변화는 LAPS의 최소 작동 고각에 상당히 민감함을 알 수 있었다. 따라서 LAPS의 위치는 LAPS의 최소 작동 고각을 최대한 낮추기 위해 최대한 대기 난류가 적으며 고고도인 지역에서 설립되어야 한다. 또한, θmin이 10°이면서 dmin이 450 km 이내일 때 SD를 한 번에 대기권 재진입 시키기 위해서는 LAPS가 SD에 가하는 가속도가 1 m/s2 이상이면 충분했다.
그리고 1 m/s2의 가속도를 A. Rubenchik et al.(2018)에서 제시된 레이저[8]를 이용하여 질량이 100 kg인 물체에 실현하기 위해서는 물체의 크기에 따라 약 34~53 Hz의 펄스 반복 빈도가 필요하였다. 이는 Japan Establishment for a Power-laser Community Harvest (J-EPoCH)의 개념적 설계, 또는 P. Mason et al.(2011)에서 제시된 diode-pumped solid state laser의 최적화된 설계[10]와 비교할 수 있다.
향후 이 결과를 기반으로 고출력 펄스 레이저 구현 기술과 고출력 펄스 레이저의 대기 중 전파에서 일어나는 비선형 효과[8], 그리고 대기 난류에 의한 레이저 펄스 분산[12]을 상쇄하기 위한 적응광학 시스템에 관한 구체적인 연구가 필요하다.