3.1 실험 개요
회로방정식 및 운동방정식에 대한 모델링 및 해석결과의 타당성 확인을 위하여 발사실험을 수행하였다. 레일건에서 나타나는 전기적 특성을 확인하기 위하여
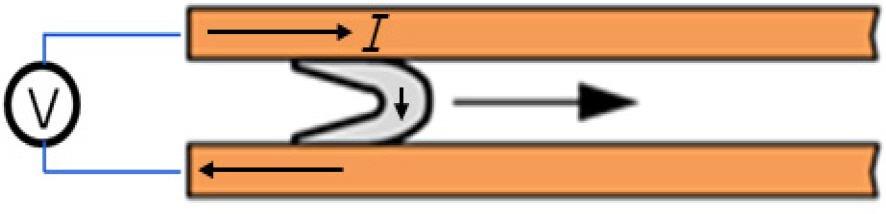
Fig. 5에서와 같이 레일건의 포미전압 및 레일에 흐르는 전류를 계측하였다. 포미전압은 상용 전압 프로브를 사용하였으며 전류계측을 위하여 로고스키 코일 프로브를 적용하였다.
Fig. 5.
Breech voltage and current
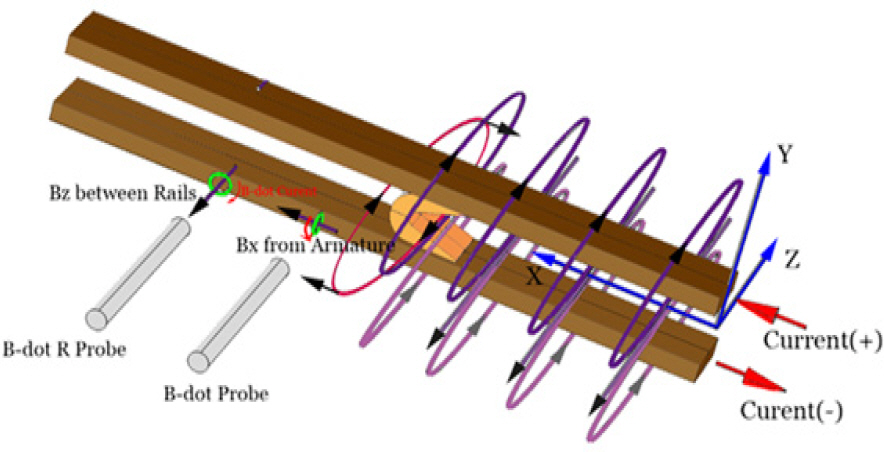
시간에 따른 발사체의 이동위치 및 속도를 계측하기 위하여
Fig. 6에서와 같이 수십 개의 B-dot 프로브를 레일건의 길이 방향으로 배치하여 사용하였다. 발사체가 각 프로브의 설치 위치에 다다르는 순간 그 프로브에 나타나는 자기장이 최대가 되는 원리를 이용한다.
Fig. 6.
Installation of B-dot probes
발사실험에 사용된 전원장치는 최대 12.8 MJ의 전기에너지를 충전할 수 있다. 이중 8 MJ은 8 개의 세그먼트로 이루어져 있고, 각 세그먼트는 10 개의 단위모듈로 구성되며 각 모듈에는 60 μH의 인덕터가 조립되어 있다. 나머지 4.8 MJ 또한 8 개의 세그먼트로 이루어지지만, 각 세그먼트는 6 개의 단위모듈로 구성되며 각 모듈에는 30 μH의 인덕터가 부착되어 있다.
이 전원장치를 레일건과 연결하고 300 그램의 발사체를 가속시켜 약 2000 m/s 이상의 포구속도를 얻기 위한 발사실험을 수행하였다. 먼저 전기회로방정식 및 가속운동방정식을 해석하여 가능한 평탄한 형상의 전류파형을 제공할 수 있는 충방전 조건을 구하였다.
Fig. 7은 12.8 MJ의 전원장치를 구성하는 128 개 전체 모듈을 4.9 kV로 충전한 후
Table 3과 같은 시간 순서로 방전했을 때 나타나는 전류, 전압, 발사체 위치 및 속도를 계측하여 해석결과와 비교한 것이다. 이때의 모듈별 방전순서는
Table 3과 같다. 해석결과는 발사체가 레일건을 이탈하는 순간까지를 나타낸 것이다.
Fig. 7에서 여러 가지 물리량들에 대한 계측 및 해석결과가 잘 일치함을 알 수 있는데, 이것은 전기회로방정식 및 발사체 가속운동방정식 모델의 타당성을 증명할 뿐 아니라 해석에 사용된 많은 상수값들이 물리적인 토대에서 비교적 정확하게 결정되었음을 보여주는 대표적인 사례라고 할 수 있다.
Fig. 7.
Comparisons of measured and predicted data
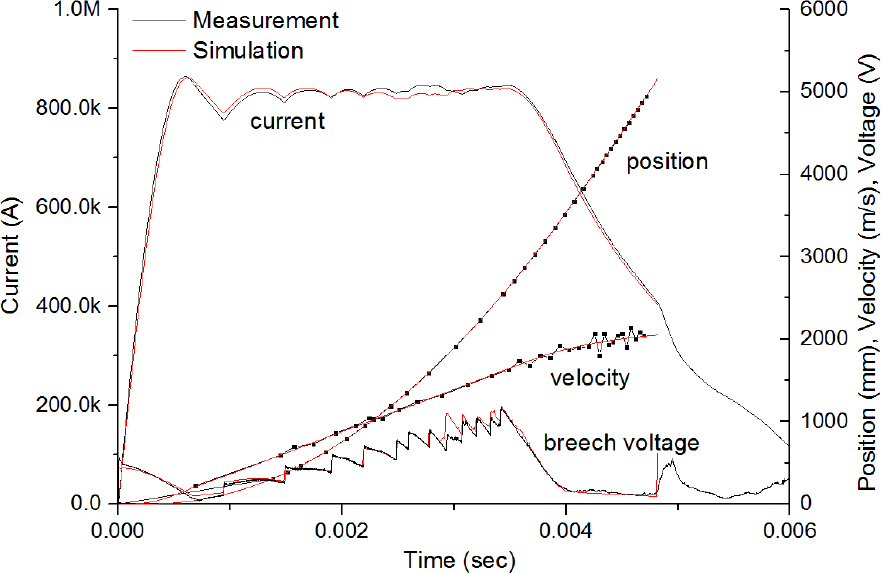
Table 3.
|
구분 |
세그먼트번호(모듈번호) |
방전시간(ms) |
|
8 MJ |
1∼4 (1∼40) |
0 |
|
5 (41∼50) |
0.94 |
|
6 (51∼60) |
1.48 |
|
7 (61∼70) |
1.90 |
|
8 (71∼80) |
2.19 |
|
4.8 MJ |
1 (1∼6) |
2.48 |
|
2 (7∼12) |
2.59 |
|
3 (13∼18) |
2.78 |
|
4 (19∼24) |
2.93 |
|
5 (25∼30) |
3.07 |
|
6 (31∼36) |
3.20 |
|
7 (37∼42) |
3.32 |
|
8 (43∼48) |
3.41 |
먼저 8 MJ 부분의 4 개 세그먼트를 동시 방전하여 약 850 kA까지 상승시키고 이 값을 유지시키기 위하여 그 다음 4 개 세그먼트를 각각 0.94, 1.48, 1.90, 2.19 ms 마다 순차적으로 방전한 후, 4.8 MJ 부분의 세그먼트 8 개를 각각 2.48, 2.59, 2.78, 2.93, 3.07, 3.20, 3.32, 3.41 ms 마다 순차적으로 방전하는 방법으로 전류파형을 형성하였다.
3.2 해석 및 실험결과 분석
Fig. 7에서와 같이 전류는 0.6 ms에서 약 850 kA에 도달한 후 정해진 시간간격에 따라 순차방전에 의하여 3.5 ms까지 평탄한 파형을 유지하고 그 시간 이후 감소해 나가며, 발사체가 레일건을 이탈하는 4.8 ms 이후 대기 중으로 아크방전이 발생하면서 급격하게 감소한다.
전류가 최대로 상승하는 0.6 ms까지의 방전초기 구간에서 발사체는 마찰력의 영향이 크기 때문에 이동거리가 매우 작다. 그러나 0.6 ms부터 3.5 ms까지의 구간에서는 높은 전류의 영향으로 이동거리가 빠르게 증가하며, 이후에는 감소하는 전류의 영향으로 증가율이 둔화됨을 볼 수 있다.
각 세그먼트의 방전시간 차이로 인하여 약 3.5 ms 까지 전류곡선이 파도모양을 나타내는데, 파고 차이가 크지 않기 때문에 (11)에서와 같이 전류의 제곱을 적분한 형태로 나타나는 속도는
Fig. 7에서와 같이 큰 변화없이 거의 선형적으로 증가하는 모양을 보이게 된다. 발사체의 속도는 전류가 유지되는 3.5 ms까지 계속적으로 증가하지만 그 이후 전류 감소와 더불어 증가율이 약화됨을 알 수 있다.
위치 및 속도 곡선에서 나타나는 점들은 발사체의 이동방향에 따라 레일건의 특정위치에 설치된 수십개의 B-dot 프로브를 사용하여 계측된 값들을 나타낸다. 이 프로브들이 설치된 위치에 발사체가 도착하는 시간을 계측하고 이것을 미분하여 평균속도를 구한 것이다. 발사체가 정지상태로부터 가속되기 시작하면 레일건에 진동이 발생한다. 발사체가 2650 mm 위치에 도달하는 3.5 ms 시간 이후부터 그 영향이 두드러지며 이에 따라 레일건에 설치된 프로브들이 좌우로 진동하면서 위치오차를 발생시킨다. 이로 인하여 시간미분으로 구해지는 속도오차가 증가하기 때문에
Fig. 7에서와 같이 진동하는 속도곡선이 나타나게 된다. 포구 가까운 곳에는 다른 곳에 비하여 프로브들이 더 촘촘하게 설치되어 있기 때문에 사격진동의 영향이 더 커서 미분오차(속도오차)가 증가함을 볼 수 있다.
레일건에 설치된 B-dot 프로브의 마지막 위치는 4950 mm 지점이며 이 위치에서의 속도는 2035 m/s이지만 발사체는 이보다 205 mm를 더 이동한 5155 mm 지점에서 레일건을 떠난다. 따라서 B-dot 프로브로는 마지막 205 mm 구간에서의 속도를 알 수 없기 때문에 계측된 속도 곡선과 일치하는 해석곡선을 이용하면 발사체가 포구를 이탈할 때의 속도는 2050 m/s가 됨을 알 수 있다.
Fig. 7에서와 같은 포미전압은 포미(breech)로부터 발사체 위치까지의 레일에 작용하는 전압과 발사체 양단에 작용하는 전압을 더한 값이다. 즉, 2.1 절의 (1)과 (2)를 더한 값으로 표시된다.
발사체에 작용하는 전압은 매우 작기 때문에 무시하면 이때 포미전압은
Fig. 8과 같은 세가지 성분으로 나누어 표시할 수 있다.
Fig. 8.
Components of breech voltage

방전초기의 전류가 상승하는 구간에서는 발사체의 이동량 및 속도가 낮은 반면, 전류변화율이 높기 때문에 Lr'(x0+x)dI/dt의 영향이 지배적이다.
전류가 일정한 수준을 유지하는 구간에서는 발사체의 이동량 및 속도가 빠르게 상승하기 때문에 Lr'x˙I 및 R′(x0+x)I의 영향이 커지므로 포미전압이 증가한다.
전류가 하강하는 구간에서는 전류변화율의 급격한 감소로 인한 Lr'(x0+x)dI/dt의 영향을 크게 받아 포미전압 또한 급격하게 감소함을 알 수 있다.
전원장치에 충전되어 있던 총에너지는 방전과 동시에 커패시터, 인덕터, 저항 등의 회로 성분들로 분산되면서 저장되거나 손실되어 나간다.
Fig. 9에서와 같이 발사체가 가속되는 특정시간에서 총에너지 E
t는 전원장치로부터 레일건 연결부까지 저장되거나 손실된 에너지 E
1 및 레일건 연결부로부터 발사체가 위치한 레일의 특정위치까지 저장되거나 손실된 에너지 E
2로 나눌 수 있다.
Fig. 9.
Energy changes of E1 and E2 during acceleration phase
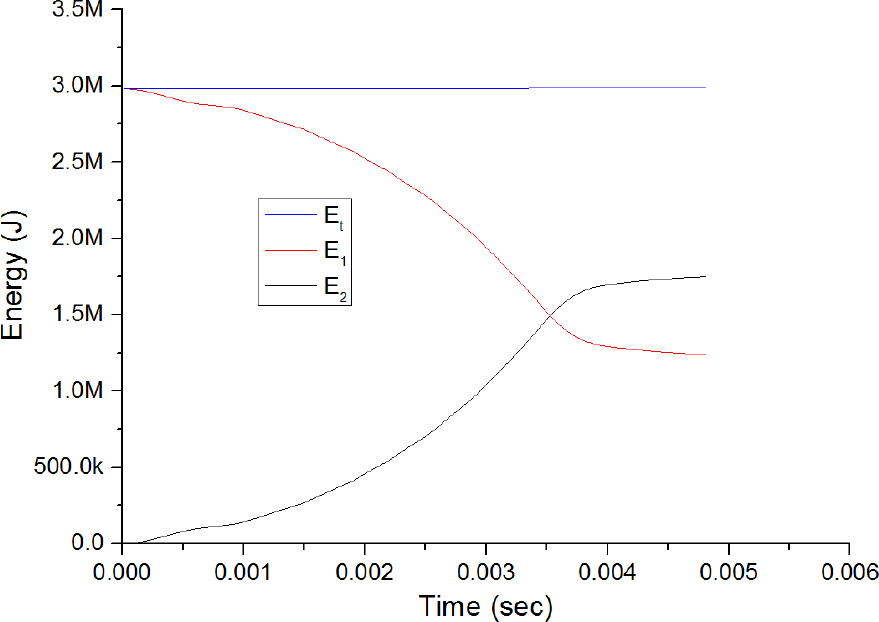
E2는 레일건 내부의 레일을 통하여 투입되는 에너지라고 할 수 있다. E2는 총에너지 Et에서 차지하는 비중이 크지만 이중 일부분만이 발사체의 운동에너지로 전환되게 된다.
(1) 및 (2)를 이용하면 레일에 투입되는 에너지 E2는 다음과 같이 쓸 수 있다.
(12)에서 레일과 발사체의 전기적 접촉상태가 양호할 경우 Varm은 Vrail에 비하여 매우 작기 때문에 무시하였다. 따라서 (12)는 다음과 같이 쓸 수 있다.
(13)에서 Er은 레일 저항열에 의하여 손실되는 에너지를 나타내고, Eu는 레일건 내부에서의 자기장에 의하여 유도되는 에너지를 나타내며 다음과 같이 전개 가능하다.
(14)에서 자기장 에너지 Eu는 발사체의 위치와 관련된 에너지(Eu1) 및 속도와 관련된 에너지(Eu2)의 합이라는 것을 알 수 있다. 여기서 Eu2는 (11)을 이용하여 다음과 같이 쓸 수 있다.
(15)에서 발사체의 속도에 의하여 유도된 자기장 에너지 Eu2는, 운동에너지(Ekin) 및 마찰에너지(Efri)와 같은 기계적 에너지로 변환된다는 것을 알 수 있다.
Table 4는 (12)∼(15)를 사용하여 발사체가 레일건을 이탈할 때(T
exit) 계산된 에너지 값들을 정리한 것이다. 총에너지(E
t) 2990 kJ 중에서 1240 kJ은 전원장치로부터 레일건 연결부까지 저장되거나 손실된 에너지(E
1)이며 나머지 1750 kJ이 레일에 투입된 에너지(E
2)이다.
Table 4.
Energy distribution at time = Texit
|
에너지 구성 |
에너지 값(kJ) |
|
Et
|
E1
|
1240 |
|
E2
|
Er
|
776.5 |
|
Eu
|
Eu1
|
230.5 |
|
Eu2
|
Ekin
|
630 |
|
Efri
|
113 |
E2 중에서 776.5 kJ은 레일 저항열에 의하여 손실된 에너지(Er)를 나타내고 나머지 973.5 kJ은 자기장에너지(Eu)가 된다.
Eu 중에서 230.5 kJ은 발사체의 위치와 관련된 자기장에너지(Eu1)이며 나머지 743 kJ은 발사체의 속도와 관련된 자기장에너지(Eu2)이다.
최종적으로 E
u2가 기계적 에너지로 변환되는데 그 중 630 kJ 만이 운동에너지(E
kin)가 되고 나머지 113 kJ은 마찰에너지(E
fri)로 손실된다.
Table 4의 경우 총에너지 2990 kJ 대비 21 %인 630 kJ이 운동에너지로 이용되었음을 알 수 있다.
방전이 시작된 시점부터 발사체가 가속되어 포구를 이탈한 후 전류가 0이 될 때까지 투입된 총에너지(Et) 중에서 운동에너지(Ekin)를 제외한 모든 에너지는 전원장치 내부 저항, 레일 저항, 아크 저항 등에 의한 저항열 및 발사체와 레일의 마찰열 등의 형태로 손실된다.