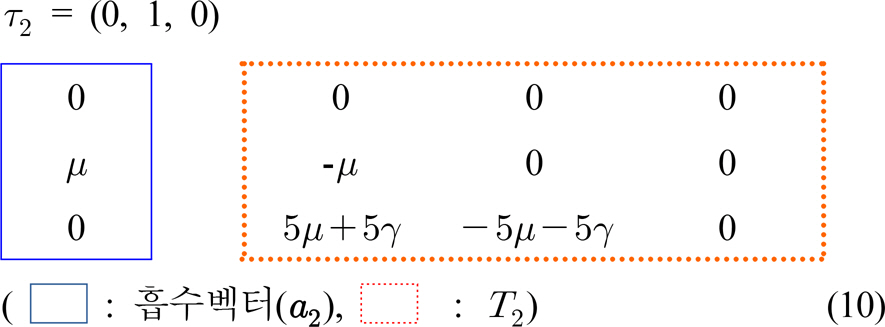ņä£ ļĪĀ
ņ░ĖņØäņä▒ ņŚåļŖö Ļ│ĀĻ░Ø(Impatient Customer)ņØĆ ļīĆĻĖ░Ē¢ēļĀ¼ ļ¼ĖņĀ£ņŚÉņä£ ņל ņĢīļĀżņ¦ä ĒśäņāüņØ┤ļŗż. ņä£ļ╣äņŖżļź╝ ļ░øĻĖ░ņ£äĒĢśņŚ¼ ņØĆĒ¢ē, ņĮ£ņä╝Ēä░, ņĀĢļ╣äĻ│Ąņן ļō▒ ņä£ļ╣äņŖż ņä╝Ēä░ņŚÉ ļÅäņ░®ĒĢ£ Ļ│ĀĻ░ØņØĆ ņ”ēņŗ£ņĀüņØĖ ņä£ļ╣äņŖżļź╝ ļ░øĻĖ░ļź╝ ņøÉĒĢśņ¦Ćļ¦ī ņä£ļ╣äņŖż ņä╝Ēä░ņØś ĒĢ£ņĀĢļÉ£ ņ×ÉņøÉ(ņŻ╝ļĪ£ ņØĖļĀź ļō▒)ņ£╝ļĪ£ ņØĖĒĢśņŚ¼ ņØ╝ņĀĢĒĢ£ ļīĆĻĖ░ņŗ£Ļ░äņØä Ļ░Ćņ¦ä Ēøä ņä£ļ╣äņŖżļź╝ ļ░øĻ▓ī ļÉ£ļŗż. ĒĢśņ¦Ćļ¦ī ļīĆĻĖ░ņŗ£Ļ░äņØ┤ ĻĖĖņ¢┤ņ¦łņłśļĪØ Ļ│ĀĻ░ØņØĆ ņ¦ĆļŻ©ĒĢ© ļō▒ņØś ņŗ¼ļ”¼ņĀü ņāüĒā£, ņØ╝ņĀĢ, ņĢĮņåŹ ļō▒ņØś Ļ░£ņØĖņé¼ņĀĢņ£╝ļĪ£ ņØĖĒĢ┤ ĻĖ░ļŗżļ”¼ļŖö ļÅäņżæņŚÉ ņä£ļ╣äņŖż ļ░øļŖö Ļ▓āņØä ĒżĻĖ░ĒĢśĻĖ░ļÅä ĒĢśĻ│Ā, ņ¢┤ļ¢ż Ļ│ĀĻ░ØņØĆ ņä£ļ╣äņŖż ņśłņāüņŗ£Ļ░äņØ┤ ĻĖĖ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉśļ®┤ ļīĆĻĖ░ņ×Éņ▓┤ļź╝ ĒĢśņ¦Ć ņĢŖņØä ņłśļÅä ņ׳ļŗż. ņØ┤ļ¤¼ĒĢ£ ĒŖ╣ņä▒ņØä Ļ░Ćņ¦ä Ļ│ĀĻ░ØņØä ļīĆĻĖ░Ē¢ēļĀ¼ ņØ┤ļĪĀņŚÉņä£ļŖö ŌĆśņ░ĖņØäņä▒ ņŚåļŖö Ļ│ĀĻ░ØŌĆÖ ņØ┤ļØ╝Ļ│Ā ņĀĢņØśĒĢśļ®░ ņØ┤ļ¤¼ĒĢ£ Ļ│ĀĻ░ØņØś Impatience ĒŖ╣ņä▒ņØä ņØ┤Ēāł(Reneging) ļ░Å ņ░©ļŗ©(Balking)ņ£╝ļĪ£ Ēæ£ĒśäĒĢ£ļŗż.
ĒŖ╣Ē׳, Ļ│ĀĻ░ØņØś ņØ┤ĒāłĻ│╝ ņ░©ļŗ©ņŚÉ Ļ┤ĆļĀ©ļÉ£ ĒŖ╣ņä▒ņØĆ ĒāĆ ļČäņĢ╝ņŚÉ ļ╣äĒĢ┤ ņŗ£Ļ░äņŚÉ ļ»╝Ļ░ÉĒĢ£ ĻĄŁļ░®ļČäņĢ╝ņŚÉ ļŗżņ¢æĒĢśĻ▓ī ņĀüņÜ®ņØ┤ Ļ░ĆļŖźĒĢśļŗż. ņØ┤ļŖö ĻĄŁļ░®ļČäņĢ╝ņŚÉņä£ļŖö ļŗżņ¢æĒĢ£ ņ░ĖņØäņä▒ ņŚåļŖö Ļ│ĀĻ░ØņØ┤ ņĪ┤ņ×¼ĒĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ņśłļź╝ ļōżļ®┤ ņ×æņĀä ņżæņŚÉ ņ£äĒŚśĒĢ£ ĒÖśĻ▓Į(ņČöļØĮ, ņ╣©ļ¬░ ļō▒)ņŚÉ ņ▓śĒĢ┤ ĻĖ┤ĻĖēĻĄ¼ņĪ░ļź╝ ņÜöņ▓ŁĒĢśļŖö ņĪ░ņóģņé¼. ĒĢ©ņĀĢ ļō▒Ļ│╝ Ļ│ĀņןņØ┤ ļ░£ņāØĒĢśņŚ¼ ĻĖ┤ĻĖē ņłśļ”¼ļź╝ ņÜöņ▓ŁĒĢśļŖö ņ×æņĀä ņÜ┤ņÜ®ļČĆļīĆ ĒĢ©ņĀĢ, ĒĢŁĻ│ĄĻĖ░, ņĀäņ░© ļō▒ņØ┤ ņ░ĖņØäņä▒ ņŚåļŖö Ļ│ĀĻ░ØņØ┤ ļÉĀ ņłś ņ׳ļŗż. ņØ┤ļ¤¼ĒĢ£ ĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢĀ ļĢī, ĻĄŁļ░®ļČäņĢ╝ņŚÉ ņ׳ņ¢┤ņä£ Impatience ĒŖ╣ņä▒ņØś Ļ│ĀļĀżĻ░Ć ĒŖ╣Ē׳ ņżæņÜöĒĢśļŗżĻ│Ā ļ¦ÉĒĢĀ ņłś ņ׳ļŗż.
ĒĢ£ĒÄĖ, ĻĄ░ņØĆ ņ×æņĀä ņÜ┤ņÜ® ļ░Å ļīĆĻĖ░ ņżæņØĖ ņĀäļĀź(ĒĢ©ņĀĢ, ĒĢŁĻ│ĄĻĖ░ ļō▒)ņØ┤ Ļ│Āņן ļ░£ņāØņ£╝ļĪ£ ņØĖĒĢśņŚ¼ ņ×æņĀä Ļ│Ąļ░▒ņØ┤ ļ░£ņāØĒĢśļŖö ĻĖ░Ļ░äņØä ņĄ£ņåīĒÖöĒĢśĻ│Ā ņ×äļ¼┤ņāüĒā£ļĪ£ ņ”ēņŗ£ ņĀäĒÖśĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äļź╝ ņÜ┤ņÜ®ĒĢśĻ│Ā ņ׳ļŗż. ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äļŖö ĻĖ┤ĻĖēņĀĢļ╣ä ņØĖļĀźņØ┤ ĒÄĖņä▒ļÉśļ®░, ĒŖ╣ņĀĢĒĢ£ ĻĖ░ĒĢ£(Impatient time) ļé┤ņŚÉ Ļ│Āņןļé£ ņןļ╣äļź╝ ņĀĢļ╣äĒĢśļŖö ņŚŁĒĢĀņØä ņłśĒ¢ēĒĢśĻ▓ī ļÉ£ļŗż. ņĀĢļ╣äņØĖļĀźņØś ĒÄĖņä▒ņØĆ ĻĄ░(ĒśäņŚŁ, ņĀĢļ╣äĻĄ░ļ¼┤ņøÉ)Ļ│╝ ļ»╝Ļ░ä(ņÖĖņŻ╝ ņÜ®ņŚŁ)ņ£╝ļĪ£ ĻĄ¼ņä▒ļÉśļ®░, ĻĄŁļ░®Ļ░£Ēśü 2.0 ļō▒ņŚÉ ņØśĒĢ┤ Ē¢źĒøä ĻĄ░ ņĀĢļ╣äņØĖļĀźņØä ĒÖĢņČ®ņŚÉ ņĀ£ĒĢ£ņØ┤ ņ׳ļŖö ĒśäņŗżņĀüņØĖ ņāüĒÖ®ņØä Ļ│ĀļĀżĒĢ£ļŗżļ®┤ ļ»╝Ļ░äĻ│╝ņØś ĒśæņŚģņØĆ ļŹöņÜ▒ ņ”ØļīĆļÉĀ Ļ▓āņ£╝ļĪ£ ĒīÉļŗ©ļÉ£ļŗż. ņØ┤ļ¤¼ĒĢ£ ņĖĪļ®┤ņØä Ļ│ĀļĀżĒĢ£ļŗżļ®┤ ņä▒Ļ│ĄņĀüņØĖ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņØś ņÜ┤ņÜ®ņØä ņ£äĒĢ┤ņä£ļŖö ĻĄ░, ļ»╝Ļ░äņØś ņĀĢļ╣äņØĖļĀź ņĄ£ņĀü ĻĘ£ļ¬©, ĒÄĖņä▒ņØĆ ņżæņÜöĒĢ£ ņÜöņåīņØ╝ Ļ▓āņØ┤ļŗż. ĒĢśņ¦Ćļ¦ī ĻĄ░ ņØśņé¼Ļ▓░ņĀĢĻČīņ×ÉļŖö ļŗżņ¢æĒĢ£ ĒÖĢļźĀņĀü ņÜöņØĖ(Ļ│Āņן/ņĀĢļ╣ä ļČäĒż, Impatience ļō▒)ņØä Ļ│ĀļĀżĒĢ£ ĒīÉļŗ©ņØ┤ ĒĢäņÜöĒĢśņ¦Ćļ¦ī ļŗ©ņł£ņ×ÉļŻī(ņŚ░Ļ░ä ļ░£ņāØĻ▒┤ņłś, ņĀĢļ╣ä ņŗ£Ļ░ä ļō▒)ļ¦īņØä Ļ│ĀļĀżĒĢśņŚ¼ ĻĖ┤ĻĖē ņĀĢļ╣äņ▓┤Ļ│äņØś ĻĄ░, ļ»╝Ļ░ä ņĀĢļ╣äņØĖļĀźņØä ĒÄĖņä▒ĒĢśĻ│Ā ņ׳ļŖö ņŗżņĀĢņØ┤ļŗż. ņØ┤ļŖö ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņØś ļ╣äĒÜ©ņ£©ņĀüņØĖ ņÜ┤ņÜ®ņ£╝ļĪ£ ņØĖĒĢ£ ĻĄŁļ░®ņśłņé░ņØś ļéŁļ╣äļĪ£ ņØ┤ņ¢┤ņ¦ł Ļ░£ņŚ░ņä▒ņØ┤ Ēü¼ļŗż.
ĒĢ£ĒÄĖ, ļīĆĻĖ░Ē¢ēļĀ¼ ņØ┤ļĪĀņØś ņĀüņÜ®ĒĢ£ ņŚ░ĻĄ¼ļŖö ļīĆļČĆļČäņØ┤ Ļ│ĀĻ░ØņØś ļīĆĻĖ░ņŗ£Ļ░ä ļČäņäØ, ļīĆĻĖ░ņŗ£Ļ░äņØä Ļ│ĀļĀżĒĢ£ ņĀüņĀĢ ņä£ļ▓äņØś ņłś(ņä£ļ╣äņŖż ĒīĆ) Ļ▓░ņĀĢ ļō▒ņŚÉ ņ¦æņżæļÉśņ¢┤ ņ׳ļŗż. ĻĘĖļ”¼Ļ│Ā Impatience Ļ│ĀĻ░ØņØä Ļ│ĀļĀżĒĢ£ ļīĆĻĖ░Ē¢ēļĀ¼ ņŚ░ĻĄ¼ļŖö Haight[1,2] ļ░Å Rao[3]Ļ░Ć ņ┤łĻĖ░ņŚ░ĻĄ¼ļź╝ ņ¦äĒ¢ēĒĢ£ ņØ┤ĒøäļĪ£ ņĄ£ĻĘ╝Ļ╣īņ¦Ć ļŗżņ¢æĒĢ£ ņŚ░ĻĄ¼ļōżņØ┤ ņ¦äĒ¢ēļÉśĻ│Ā ņ׳ņ£╝ļ®░[4,5], Wang ļō▒[6]ņØĆ Impatience Ļ│ĀĻ░ØņØś Ē¢ēļÅÖ Ēī©Ēä┤(Reneging, Balking)Ļ│╝ ĒĢ┤ļ▓ĢņŚÉ ļīĆĒĢśņŚ¼ ĻĖ░ņłĀĒĢ£ ņä£ļ▓ĀņØ┤ ņŚ░ĻĄ¼ļź╝ ņ¦äĒ¢ēĒĢśņśĆļŗż. ļ╣äļĪØ Impatient customerĻ░Ć ņĪ┤ņ×¼ĒĢśļŖö ļīĆĻĖ░Ē¢ēļĀ¼ņŚÉ ļīĆĒĢ£ ņŚ░ĻĄ¼ļŖö Ļ│ĀĻ░ØņØś ņ¦ĆņłśļÅäņ░®, ļ¦łņĮöļ╣äņĢł ļÅäņ░®, ļŗ©Ļ│äĒśĢ ņä£ļ╣äņŖż ļō▒ ļ¦ÄņØĆ ņŚ░ĻĄ¼Ļ░Ć ņ¦äĒ¢ēļÉśņŚłņ¦Ćļ¦ī, ņØ╝ļČĆ ņĮ£ņä╝Ēä░ļČäņĢ╝ņŚÉ ņĀüņÜ®ļÉ£ ņŚ░ĻĄ¼ļź╝ ņĀ£ņÖĖĒĢśĻ│ĀļŖö ļīĆļČĆļČä ĒåĄņŗĀļČäņĢ╝ņŚÉ ņ¦æņżæļÉśņ¢┤ ņ׳ļŗż. ĻĄŁļ░®ļČäņĢ╝ņŚÉ ņĀüņÜ®ļÉ£ ņŚ░ĻĄ¼ļź╝ ņé┤ĒÄ┤ļ│┤ļ®┤ Impatience ĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢśņŚ¼ ĻĖ┤ĻĖē ņĀĢļ╣äņŗ£ņŖżĒģ£ņØś ĻĖ┤ĻĖē ņĀĢļ╣äņØĖļĀź ņłśņżĆņŚÉ Ļ┤ĆĒĢśņŚ¼ ĻĄ░ ņĀĢļ╣äņØĖļĀźņØä ļīĆņāüņ£╝ļĪ£ ļČäņäØĒĢ£ ņŚ░ĻĄ¼[10]ņÖĆ ņĪ░ņóģņé¼ ĻĄ¼ņĪ░ļź╝ ņ£äĒĢ£ ņĄ£ņĀü ņ×æņĀäĒīĆ ņłśņżĆņØä ļČäņäØĒĢ£ ņŚ░ĻĄ¼[11,12] ļō▒ņØä ņĀ£ņÖĖĒĢśĻ│ĀļŖö ņ░ŠņĢäļ│┤ĻĖ░ Ēלļōżļŗż. ņ£äņØś ĻĄŁļ░®ļČäņĢ╝ņŚÉ ņĀüņÜ®ļÉ£ ņŚ░ĻĄ¼ļōżņØś ļ¬©ĒśĢņØĆ ImpatienceņØś ĒŖ╣ņä▒ņØä Ļ░Ćņ¦ä Ļ│ĀĻ░ØļÅäņ░®(ņĀĢļ╣äņÜöņ▓Ł, ĻĄ¼ņĪ░ņÜöņ▓Ł)ņØ┤ ĒżņĢäņåĪĻ│╝ņĀĢņ£╝ļĪ£ ļ░£ņāØĒĢśĻ│Ā ņä£ļ╣äņŖż ņŗ£Ļ░ä, ņ░©ļŗ© ļ░Å ņØ┤ĒāłņØ┤ ņ¦ĆņłśļČäĒżļĪ£ ļ░£ņāØĒĢ£ļŗżĻ│Ā Ļ░ĆņĀĢĒĢśņŚ¼ ļ│Ė ņŚ░ĻĄ¼ņØś ļ¬©ĒśĢĻ│╝ ņ£Āņé¼ĒĢ£ ĒŖ╣ņ¦ĢņØ┤ ņ׳ņ¦Ćļ¦ī, ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ ļČäņäØĒĢśĻ│Āņ×É ĒĢśļŖö Ļ░üņ×É ļŗżļźĖ ĒŖ╣ņä▒(ņä£ļ╣äņŖż ņŗ£Ļ░ä)ņØä Ļ░Ćņ¦ä ņä£ļ▓äļōż(ĻĄ░ ļ░Å ļ»╝Ļ░ä ņĀĢļ╣äņØĖļĀź)Ļ░äņØś ĒśæņŚģ(Pooling)ņŚÉ ļīĆĒĢ£ ĒĢ┤ļ▓ĢņØä ņĀ£ņŗ£ĒĢśņ¦ĆļŖö ļ¬╗ĒĢśļŖö ĒĢ£Ļ│äĻ░Ć ņ׳ļŗż. ņØ┤ļ¤¼ĒĢ£ ļČĆļČäņØ┤ ļ¬©ĒśĢņĀüņØĖ ņĖĪļ®┤ņŚÉņä£ ĻĖ░ņĪ┤ņŚ░ĻĄ¼ņÖĆņØś ņ░©ļ│äņä▒ņØ┤ ņ׳ļŗżĻ│Ā ĒĢĀ ņłś ņ׳ļŗż.
ņ£äņØś ĻĖ░ņłĀļÉ£ ļ░öļź╝ ļ░öĒāĢņ£╝ļĪ£ ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņØś ĻĄ░ ļ░Å ļ»╝Ļ░ä ņĀĢļ╣äņØĖļĀźņØś ņĀüņĀĢ ĻĘ£ļ¬©, ĒÄĖņä▒ Ļ▓░ņĀĢņØä ņ£äĒĢśņŚ¼ Impatience ĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢ£ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņØś ņØĖļĀźņØä ņĄ£ņĀüņ£╝ļĪ£ ĒĢĀļŗ╣ĒĢĀ ņłś ņ׳ļŖö ļ¬©ļŹĖņØä ņĀ£ņŗ£ĒĢ£ļŗż.
ļ│Ė ņŚ░ĻĄ¼ļŖö ļŗżņØīĻ│╝ Ļ░ÖņØ┤ ĻĄ¼ņä▒ļÉśņ¢┤ ņ׳ļŗż. 2ņןņŚÉņä£ļŖö ĻĖ┤ĻĖē ņĀĢļ╣äņ▓┤Ļ│ä ļČäņäØņŚÉ ĒĢäņÜöĒĢ£ ņŻ╝ņÜö ņØ┤ļĪĀņØä ņĀĢļ”¼ĒĢ£ļŗż. 3ņןņŚÉņä£ļŖö ĻĖ┤ĻĖē ņĀĢļ╣äņä▒Ļ│ĄĒÖĢļźĀņØä ņĄ£ļīĆĒÖöĒĢśĻĖ░ ņ£äĒĢ£ ĻĖ┤ĻĖēņĀĢļ╣äņŗ£ņŖżĒģ£ņØś ļČäņäØ ļ¬©ļŹĖņØä ņĀ£ņŗ£ĒĢ£ļŗż. ĻĘĖļ”¼Ļ│Ā 4ņןņŚÉņä£ļŖö ļČäņäØ ļ¬©ļŹĖņØä ļ░öĒāĢņ£╝ļĪ£ ņłśņ╣śņŗżĒŚś ļ░Å Ļ▓░Ļ│╝ļź╝ ļČäņäØĒĢśņśĆļŗż.
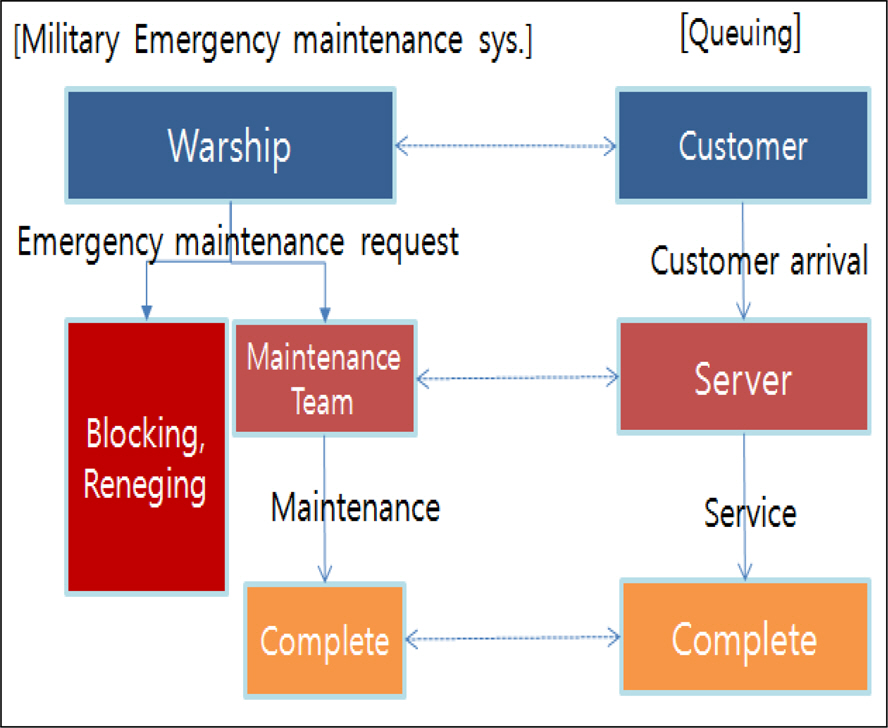
ņØ┤ļĪĀņĀü ļ░░Ļ▓Į
2.1 ĻĖ┤ĻĖē ņĀĢļ╣äņŗ£ņŖżĒģ£ ņä▒ļŖź
ĻĖ┤ĻĖē ņĀĢļ╣äņŗ£ņŖżĒģ£ņØĆ ņ×æņĀä ņżæņØĖ ņĀäļĀźņŚÉ Ļ│ĀņןņØ┤ ļ░£ņāØĒĢśļ®┤ ņ×æņĀä Ļ│Ąļ░▒ņØś ņĄ£ņåīĒÖöļź╝ ņ£äĒĢ┤ ņØ╝ņĀĢ ņŗ£Ļ░ä ņĢłņŚÉ ņĀĢļ╣äļź╝ ņÖäļŻīĒĢśļŖö ņ▓┤Ļ│äņØ┤ļŗż. ĻĖ┤ĻĖē ņĀĢļ╣äņŗ£ņŖżĒģ£ņØĆ ņ░ĖņØäņä▒ ņŚåļŖö Ļ│ĀĻ░ØņØ┤ ņ׳ļŖö ļīĆĻĖ░Ē¢ēļĀ¼ ļ¬©ļŹĖņØä ņĀüņÜ®ĒĢśņŚ¼ ļČäņäØĒĢĀ ņłś ņ׳ļŖö ļŹ░, ņØ┤ļŖö Fig. 1Ļ│╝ Ļ░ÖņØ┤ Ļ│ĀĻ░ØņØś ļÅäņ░®ņØĆ ĻĖ┤ĻĖēņĀĢļ╣äņÜöņ▓Ł, ņä£ļ▓äļŖö ĻĖ┤ĻĖēņĀĢļ╣äĒīĆ, ņä£ļ╣äņŖżņÖäļŻīļŖö ņĀĢļ╣äņÖäļŻīņÖĆ ļÅÖņØ╝ĒĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż.
ņØ┤ļ¤¼ĒĢ£ ĻĖ┤ĻĖēņĀĢļ╣äņŗ£ņŖżĒģ£ņØś ņä▒ļŖźņØĆ ĻĖ┤ĻĖēņĀĢļ╣äņÜöņ▓ŁņØ┤ ņĀæņłśļÉśņŚłņØä ļĢī ņĀĢļ╣äņØĖļĀźņØś ļČĆņĪ▒ņ£╝ļĪ£ ņ░©ļŗ©ļÉśņ¦Ć ņĢŖĻ│Ā, ņØ╝ņĀĢĒĢ£ ņŗ£Ļ░ä ņØ┤ļé┤ņŚÉ ņĀĢļ╣äļź╝ ņÖäļŻīĒĢĀ ņłś ņ׳ļŖö ĒÖĢļźĀņØ┤ļŗż. ņØ┤ļĢī ļīĆĻĖ░ņŗ£Ļ░ä, ņĀĢļ╣äņŗ£Ļ░ä ļ░Å ņĀĢļ╣ä ņÖäļŻī ņÜöĻĄ¼ ņŗ£Ļ░äņØĆ Ļ│Āņןļ╣łļÅä, ņĀĢļ╣äļŖźļĀź, ņ×æņĀäĒÖśĻ▓ĮņŚÉ ņØśĒĢ┤ ļ│ĆĒÖöļÉśļŖö ĒÖĢļźĀ ļ│ĆņłśņØ┤ļ®░ ņĀĢļ╣äņÖäļŻī ņÜöĻĄ¼ņŗ£Ļ░äņØä ĒÖĢļźĀļ│Ćņłś Y1 ļ░Å ņĀĢļ╣äņÖäļŻīņŗ£ Ļ╣īņ¦Ć ņåīņÜöļÉśļŖö ņŗ£Ļ░äņØäY2ļØ╝Ļ│Ā ņĀĢņØśĒĢśļ®┤ Y2ļŖö ļīĆĻĖ░ņŗ£Ļ░äĻ│╝ ņĀĢļ╣äņŗ£Ļ░äņØś ĒĢ®ņ£╝ļĪ£ ļæÉ ĒÖĢļźĀļ│ĆņłśņØś ĒĢ®ņØ┤ ļÉśļ»ĆļĪ£ ļŗ©Ļ│äĒśĢ ļČäĒż(Phase type Distribution)Ļ░Ć ļÉ£ļŗż. ļö░ļØ╝ņä£ ĻĖ┤ĻĖēņĀĢļ╣äņŗ£ņŖżĒģ£ņØś ņä▒ļŖźņ▓ÖļÅä ņ”ē, ņĀĢļ╣äņä▒Ļ│ĄļźĀņØĆ ņĀĢļ╣äņÖäļŻī ņŗ£ Ļ╣īņ¦Ć ņåīņÜöļÉśļŖö ņŗ£Ļ░äļ│┤ļŗż ņĀĢļ╣äņÖäļŻī ņÜöĻĄ¼ņŗ£Ļ░äņØ┤ ņ¦¦ņ£╝ļ®┤ ņĀĢļ╣äĻ░Ć ņä▒Ļ│ĄĒĢśļŖö Ļ▓ĮņÜ░ņØ┤Ļ│Ā ņØ┤ļŖö min (Y1, Y2)ņØś ļČäĒżļź╝ ĻĄ¼ĒĢśļ®┤ ļÅäņČ£ĒĢĀ ņłś ņ׳ļŗż.
2.2 ļŗ©Ļ│äĒśĢ ļČäĒżņÖĆ ņĄ£ņåīļČäĒż
ļŗ©Ļ│äĒśĢ ļČäĒżļŖö ļÅäņ░®Ļ│╝ ņä£ļ╣äņŖżļź╝ ņ¦ĆņłśļČäĒżņØś ņżæĒĢ® Ēś╣ņØĆ Ēś╝ĒĢ® ĒśĢĒā£ļĪ£ Ēæ£ĒśäĻ░ĆļŖźĒĢśĻ│Ā ņ¦ĆņłśļČäĒżĻ░Ć Ēæ£ĒśäĒĢĀ ņłś ņŚåļŖö ļŗżņ¢æĒĢ£ ļČäĒżļź╝ ĻĘ╝ņé¼ĒĢĀ ņłś ņ׳ļŖö ĒÖĢļźĀ ļČäĒżļØ╝ļŖö ĒŖ╣ņä▒Ļ│╝ ņŚ░ņé░ ņĢīĻ│Āļ”¼ņ”śņØä ņĀ£Ļ│ĄĒĢ£ļŗżļŖö ņןņĀÉņØ┤ ņ׳ņ¢┤ ņĄ£ņ┤łņØś ņŚ░ĻĄ¼Ļ░Ć ņ¦äĒ¢ēļÉ£ ņØ┤ĒøäņŚÉ ļŗżņ¢æĒĢ£ ĒÖĢļźĀņĀü Ēśäņāü ļČäņäØņŚÉ ĒÖ£ņÜ®ļÉśĻ│Ā ņ׳ļŗż[10].
ļŗ©Ļ│äĒśĢ ļČäĒżļŖö ĒĢśļéśņØś ĒØĪņłśņāüĒā£ņÖĆ ņ┤łĻĖ░ņāüĒā£ ĒÖĢļźĀņØä Ļ░¢ļŖö ņŚ░ņłśņŗ£Ļ░ä ļ¦łņĮöĒöäņ▓┤ņØĖņØ┤ ņ׳ņØä ļĢī ņ┤łĻĖ░ņāüĒā£ņŚÉņä£ ĒØĪņłśļÉĀ ļĢī Ļ╣īņ¦Ć Ļ▒Ėļ”░ ņŗ£Ļ░äņØś ļČäĒżņØ┤ļŗż. ņØ┤ļĢī ņāüĒā£Ļ│ĄĻ░ä s={0,1,2,...n}ņØ┤Ļ│Ā ņāüĒā£(state) 0ņØĆ ĒØĪņłśņāüĒā£ (Absorbing State) ļ░Å ļéśļ©Ėņ¦Ć ņāüĒā£Ļ│ĄĻ░äņØĆ ņØ╝ņŗ£ņāüĒā£(Transient State)ņØĖ ĒØĪņłśļ¦łņĮöĒöäņ▓┤ņØĖņØ┤ ņŗØ (1)Ļ│╝ Ļ░ÖņØ┤ ĻĄ¼ņä▒ļÉ£ļŗżĻ│Ā Ļ░ĆņĀĢĒĢśņ×É.
ņŗØ (1)ņŚÉņä£ aļŖö Ēü¼ĻĖ░Ļ░Ć mņØĖ ņŚ┤ļ▓ĪĒä░ļĪ£ Ļ░ü ņØ╝ņŗ£ņāüĒā£ņŚÉņä£ ĒØĪņłśņāüĒā£ļĪ£ņØś ņĀäņØ┤ņ£©ņØä ņØśļ»ĖĒĢ£ļŗż. ļŗżņŗ£ ļ¦ÉĒĢśļ®┤ Ļ│ĀņןņØ┤ ļ░£ņāØĒĢśĻ▒░ļéś, ņä£ļ╣äņŖżĻ░Ć ņÖäļŻīļÉśļŖö ņĀäņØ┤ņ£©ņØ┤ļŗż. RļŖö ņØ╝ņŗ£ņāüĒā£(Transient State)ņŚÉņä£ņØś ņĀäņØ┤ļź╝ ļéśĒāĆļé┤ļŖö mņ░©ņøÉņØś ņĀäņØ┤ņ£© Ē¢ēļĀ¼ņØ┤ļ®░ Ļ│ĀņןņØ┤ļéś ņä£ļ╣äņŖżĻ░Ć ņÖäļŻīļÉśĻĖ░ ņĀäņŚÉ ņāüĒā£Ļ│ĄĻ░äņŚÉņä£ņØś ņĀäņØ┤ņ£©ņØä ņØśļ»ĖĒĢ£ļŗż.
ĒĢ£ĒÄĖ, ŽäņØĆ ņ┤łĻĖ░ĒÖĢļźĀļĪ£ņä£ ĒÖĢļźĀĻ│╝ņĀĢņØ┤ ņŗ£ņ×æļÉśļŖö ņØ╝ņŗ£ņāüĒā£ļź╝ ļéśĒāĆļé┤ļ®░ mņ░©ņøÉ Ē¢ē ļ▓ĪĒä░(row vector)ņØ┤ļ®░, ļ¦łņĮöĒöäņ▓┤ņØĖņØś ĒŖ╣ņä▒ņāü ļ¬©ļōĀ Ē¢ēņØś ĒĢ®ņØĆ 0ņØ┤ļ®░, ņ┤łĻĖ░ĒÖĢļźĀņØś ĒĢ®ņØĆ 1ņØ┤ļŗż. ļ▓ĪĒä░ ŽäņŚÉ ņØśĒĢ┤ ņ┤łĻĖ░ĒÖĢļźĀņØ┤ Ļ▓░ņĀĢļÉ£ļŗżĻ│Ā Ļ░ĆņĀĢĒĢśļ®┤, ĒÖĢļźĀ ļ│Ćņłś YļŖö PH(Žä, R)ļĪ£ Ēæ£ĒśäļÉ£ļŗż[9].
ĻĘĖļ”¼Ļ│Ā ĒŖ╣ņĀĢ ņŗ£ņĀÉ tņŚÉņä£ ĒÖĢļźĀ ļ│Ćņłś YĻ░Ć ļŗ©Ļ│äĒśĢ ļČäĒżļź╝ ļö░ļź╝ ļĢī, ļČäĒż ĒĢ©ņłś(Distribution Function)ļŖö ņŗØ (2)ņÖĆ Ļ░ÖņØ┤ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż.
ņØ┤ļĢī, 1ņØĆ ļ¬©ļōĀ ņøÉņåīĻ░Ć 1ņØĖ ĒĢ® ļ▓ĪĒä░(Sum Vector)ļź╝ ņØśļ»ĖĒĢśĻ│Ā, ņŗØ (2)ņÖĆ -RŌłÖ1 = aļØ╝ļŖö ņé¼ņŗżņØä ĒÖ£ņÜ®ĒĢśļ®┤ ļŗ©Ļ│äĒśĢ ĒÖĢļźĀ ļČäĒżņØś ĒÖĢļźĀļ░ĆļÅäĒĢ©ņłś(Probability Density Function)ļŖö ņŗØ (3)Ļ│╝ Ļ░ÖņØ┤ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż.
ņØ╝ņŗ£ņāüĒā£ņŚÉņä£ ĒØĪņłśņāüĒā£ļĪ£ ņĀäņØ┤ļÉśļŖö ņĀäņØ┤ņ£© ļ▓ĪĒä░ļź╝ Ļ░üĻ░ü a1, a2 ļ░Å ļæÉ ĒÖĢļźĀļ│Ćņłś Y1, Y2Ļ░Ć ņä£ļĪ£ ļÅģļ”ĮņØ┤ļ®░ Ļ░üĻ░ü(Žä1, R1), (Žä2, R2)ņØĖ ļŗ©Ļ│äĒśĢ ļČäĒżļź╝ ļö░ļźĖļŗżĻ│Ā ņĀĢņØśĒĢśļ®┤ ņĀĢļ╣äņä▒Ļ│ĄĒÖĢļźĀņØĖ Pr[Y1 > Y2]ļŖö ņŗØ (4)ņÖĆ Ļ░ÖņØ┤ ņ£ĀļÅäļÉ£ļŗż[8].
fY2(t) ņŚÉ ņŗØ (3)ņØä ļīĆņ×ģĒĢśĻ│Ā Kronecker Ļ│▒Ļ│╝ ĒĢ®ņØś ĒŖ╣ņä▒ņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņĀĢļ”¼ĒĢśļ®┤ ņŗØ (4)ļŖö ņŗØ (5)ņÖĆ Ļ░ÖņØ┤ ņ£ĀļÅäĒĢĀ ņłś ņ׳ļŗż.
ŌŖŚ, ŌŖĢļŖö Kronecker Ļ│▒Ļ│╝ ĒĢ®ņØä ļéśĒāĆļé┤ļŖö ĻĖ░ĒśĖņØ┤ļ®░, Graham[11]ņØś ņŚ░ĻĄ¼ņŚÉņä£ KroneckerņØś ņĀĢņØś ļ░Å ĒŖ╣ņä▒ņØä ĻĖ░ņłĀĒĢśņśĆļŗż.
ĒĢ£ĒÄĖ, ļ│Ė ņŚ░ĻĄ¼ņÖĆ Ļ░ÖņØĆ ņ░ĖņØäņä▒ ņŚåļŖö Ļ│ĀĻ░ØņØś m/m/cļīĆĻĖ░Ē¢ēļĀ¼ ļ¬©ĒśĢņŚÉņä£ ╬╗ļź╝ Ļ│ĀĻ░Ø ļÅäņ░®ļźĀ, ╬│ļź╝ ņ░ĖņØäņä▒ ļČäĒż(Impatience rate), ╬╝ļź╝ ņä£ļ╣äņŖżņ£©, Pcļź╝ C ņä£ļ▓äņŚÉ Ļ│ĀĻ░ØņØ┤ ņ׳ņØä ĒÖĢļźĀņØ┤ļØ╝Ļ│Ā ņĀĢņØśĒĢśļ®┤, ņØ┤Ēāł(Reneging) ļ░Å ņ░©ļŗ©(Blocking)ļÉśļŖö Ļ│ĀĻ░ØņØś ļČäĒżļŖö ņ¦ĆņłśļČäĒżļź╝ ļö░ļź┤ļ®░ ņŗØ (6)Ļ│╝ Ļ░ÖņØ┤ Ēæ£ĒśäļÉ£ļŗż[12].
ĻĖ┤ĻĖēņĀĢļ╣äņŗ£ņŖżĒģ£ ļČäņäØļ¬©ļŹĖ
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņØś ĻĄ░ ļ░Å ļ»╝Ļ░ä ņĀĢļ╣äņØĖļĀźņØś ņĀüņĀĢ ĻĘ£ļ¬©, ĒÄĖņä▒ Ļ▓░ņĀĢņØä ņ£äĒĢśņŚ¼ Impatience ĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢ£ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņØś ņä▒ļŖźļČäņäØ ļ¬©ļŹĖņØä ņĀ£ņŗ£ĒĢ£ļŗż. ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņØś ņä▒ļŖźļČäņäØ ļ¬©ļŹĖņØĆ ļ»╝Ļ░äņØĖļĀź(ņÖĖņŻ╝ņÜ®ņŚŁ)ņØ┤ ĻĄ░(ĒśäņŚŁ, ĻĄ░ļ¼┤ņøÉ) ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņŚÉ ĒżĒĢ©ļÉśņ¢┤ ĒśæņŚģĒĢśļŖö ļ¬©ļŹĖ(ņØ┤ĒĢś Aļ¬©ļŹĖ)Ļ│╝ ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņŚÉņä£ ņÜ░ņäĀ ņĀĢļ╣äļź╝ ņŗżņŗ£ĒĢśĻ│Ā ņŚ¼ļĀźļČĆņĪ▒ ļō▒ņ£╝ļĪ£ ļ»╝Ļ░äņØĖļĀź(ņÖĖņŻ╝ņÜ®ņŚŁ)ņØ┤ ĒśæņŚģĒĢśļŖö ļ¬©ļŹĖ(ņØ┤ĒĢś B) 2Ļ░Ćņ¦ĆļĪ£ ĻĄ¼ļČäĒĢśņŚ¼ ļČäņäØ ļ¬©ĒśĢņØä ņĀ£ņŗ£ĒĢ£ļŗż.
3.1 ņŚ░ĻĄ¼ļ¬©ĒśĢņØś Ļ░ĆņĀĢ
ļ│Ė ņŚ░ĻĄ¼ļ¬©ĒśĢņØś ņŻ╝ņÜö Ļ░ĆņĀĢņØĆ ļŗżņØīĻ│╝ Ļ░Öļŗż.
ņ▓½ņ¦Ė, ĻĖ┤ĻĖē ņĀĢļ╣äĻ░Ć ņÜöĻĄ¼ļÉśļŖö ņŻ╝ņÜö ņןļ╣äņØś Ļ│Āņן ļ░£ņāØļźĀņØĆ ĒżņĢäņåĪ Ļ│╝ņĀĢ(Poisson Process)ļĪ£ ļ░£ņāØĒĢ£ļŗż. ļæśņ¦Ė, ĻĖ┤ĻĖē ņĀĢļ╣äņŗ£Ļ░äņØĆ ņĀĢļ╣äļ¤ē, ņĀĢļ╣ä ļé£ņØ┤ļÅäņŚÉ ļö░ļØ╝ Ļ▓░ņĀĢļÉśĻ│Ā ņ¦ĆņłśļČäĒżļź╝ ļö░ļźĖļŗż. ņģŗņ¦Ė, ņĀĢļ╣ä ņÖäļŻī ņÜöĻĄ¼ ņŗ£Ļ░äņØĆ ņżæņÜöņä▒ ļ░Å ņóģļźś, ņ×æņĀä ĒÖśĻ▓Į ļō▒ņŚÉ ļö░ļØ╝ Ļ▓░ņĀĢļÉśņ¢┤ ņ¦Ćņłś ļČäĒżļź╝ ļö░ļźĖļŗż. ļäĘņ¦Ė, ņØ┤Ēāł ļ░Å ņ░©ļŗ©ļÉśļŖö Ļ│ĀĻ░ØņØś ļČäĒżļŖö Ļ│ĀĻ░Øļ░£ņāØņØ┤ ĒżņĢäņåĪ Ļ│╝ņĀĢ, ņä£ļ╣äņŖżĻ░Ć ņ¦ĆņłśļČäĒżņØĖ m/m/cļ¬©ļŹĖņŚÉņä£ ņ¦ĆņłśļČäĒżļź╝ ļö░ļźĖļŗż. ĻĘĖļ”¼Ļ│Ā ļ│Ė ņŚ░ĻĄ¼ņØś ļ¬©ĒśĢņØĆ ļŗżņØīĻ│╝ Ļ░ÖņØĆ ĻĖ░ĒśĖļź╝ ņé¼ņÜ®ĒĢ£ļŗż. ĻĖ┤ĻĖē ņĀĢļ╣ä ņÜöņ▓Ł ļÅäņ░®ļźĀ(Arrival rate)ņØä ╬╗, ĻĖ┤ĻĖē ņĀĢļ╣ä ņä£ļ╣äņŖżņ£©(Service rate)ņØä ╬╝, ņĀĢļ╣ä ņÖäļŻī ņÜöĻĄ¼ņ£©(Impatient rate)ņØä ╬│. ĻĘĖļ”¼Ļ│Ā ĻĄ░ ļ░Å ļ»╝Ļ░ä ĻĖ┤ĻĖē ņĀĢļ╣äĒīĆ ņłś(Server)ļź╝ c1, c2ļĪ£ Ēæ£ĒśäĒĢśņśĆļŗż.
3.2 ļČäņäØļ¬©ļŹĖ
ĻĄ░ņŚÉņä£ ĻĖ┤ĻĖē ņĀĢļ╣äņŗ£ņŖżĒģ£ņØä ņÜ┤ņÜ®ĒĢĀ ļĢī, Ļ│Āņןļé£ ņןļ╣äņØś ĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢśĻĖ░ ņ£äĒĢśņŚ¼ ļ¬©ļŹĖ AņÖĆ ļ¬©ļŹĖ Bļź╝ ĻĄ¼ļČäĒĢśņŚ¼ ļČäņäØņØä ņŗżņŗ£ĒĢśņśĆļŗż. ļ¬©ļŹĖ AņÖĆ ļ¬©ļŹĖ Bļź╝ ĻĄ¼ļČäĒĢśļŖö ņØ┤ņ£ĀļŖö Ļ│Āņןļé£ ņןļ╣äĻ░Ć ņ×æņĀäņĀäļĀźņØś ļ│┤ņĢłĻĄ¼ņŚŁ(ļ»╝Ļ░äņØĖņØ┤ ņČ£ņ×ģņØ┤ ĻĖłņ¦ĆļÉ£ ĻĄ¼ņŚŁ) ņØ┤ņÖĖņŚÉ ņ£äņ╣śĒĢśĻ│Ā ņ׳ņ£╝ļ®┤ ĻĄ░Ļ│╝ ļ»╝Ļ░ä ņØĖļĀźņØ┤ ĒśæņŚģĒĢśņŚ¼ ĻĖ┤ĻĖēņĀĢļ╣äļź╝ ņŗżņŗ£ĒĢśļ®┤ ļÉśņ¦Ćļ¦ī, ļ│┤ņĢłĻĄ¼ņŚŁ ļé┤ņØś ņ£äņ╣śĒĢ£ ņןļ╣äņŚÉ Ļ│ĀņןņØ┤ ļ░£ņāØĒĢśĻ▓ī ļÉśļ®┤ ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äņØĖļĀźņØ┤ ņÜ░ņäĀ ņĀĢļ╣äļź╝ ņŗżņŗ£ĒĢśĻ│Ā ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äņØĖļĀźņØś ņŚ¼ļĀź ļČĆņĪ▒ ļō▒ņ£╝ļĪ£ ņÜöĻĄ¼ņŗ£Ļ░ä ļé┤ņŚÉ ņĀĢļ╣äļź╝ ņŗżņŗ£ĒĢśņ¦Ć ļ¬╗ĒĢśļŖö Ļ▓ĮņÜ░ņŚÉļŖö ņןļ╣äļź╝ ļ│┤ņĢłĻĄ¼ņŚŁņŚÉņä£ ņØ╝ļ░śĻĄ¼ņŚŁņ£╝ļĪ£ ņØ┤ļÅÖņŗ£ņ╝£ ļ»╝Ļ░ä ĻĖ┤ĻĖēņĀĢļ╣äĒīĆņØ┤ ņĀĢļ╣äļź╝ ņŗżņŗ£ĒĢśņŚ¼ņĢ╝ ĒĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż.
3.2.1 ļ¬©ļŹĖ A: ļ»╝Ļ░äņØĖļĀźņØ┤ ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņŚÉ ĒżĒĢ©ļÉ£ ļ¬©ĒśĢ
ļ¬©ļŹĖ A ņŗ£ņØś ĻĖ┤ĻĖēņĀĢļ╣äĒīĆ ņÜ┤ņÜ®ņØĆ Fig. 2ņÖĆ Ļ░ÖņØ┤ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż. ņ×æņĀä ņĀäļĀźņŚÉņä£ ĒżņĢäņåĪ Ļ│╝ņĀĢņ£╝ļĪ£ ņןļ╣äĻ│Āņן(╬╗)ņØ┤ ļ░£ņāØĒĢśļ®┤ ĻĄ░ ņĀĢļ╣äĒīĆĻ│╝ ļ»╝Ļ░ä ņĀĢļ╣äĒīĆņØ┤ ĒśæņŚģĒĢśņŚ¼ ņ¦ĆņłśļČäĒż(╬╝)ļĪ£ ņĀĢļ╣äļź╝ ņŗżņŗ£ĒĢśĻ▓ī ļÉśĻ│Ā ņĀĢļ╣äļź╝ ņÖäļŻīĒĢ┤ņĢ╝ ļÉśļŖö ņŗ£Ļ░äņØĆ ╬│ņØś ņØ┤Ēāłņ£©ņØä Ļ░Ćņ¦ĆļŖö ņ¦ĆņłśļČäĒżļź╝ ļö░ļź┤Ļ▓ī ļÉ£ļŗż.
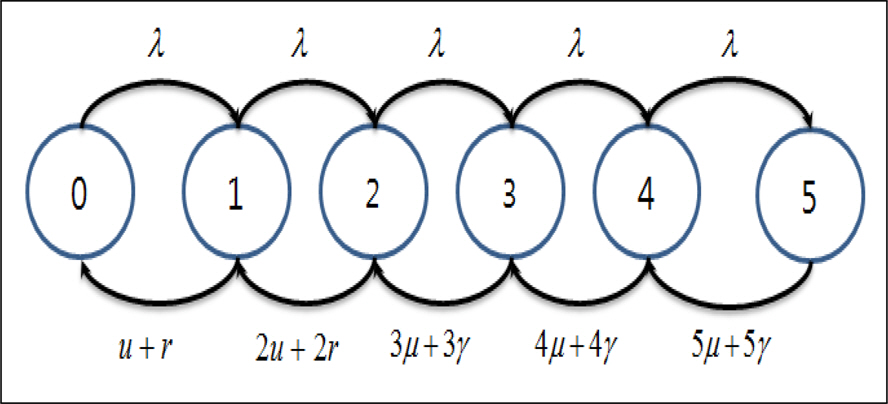
ņĀäņØ┤ņ£© Ē¢ēļĀ¼ņØä ĻĄ¼ņä▒ĒĢśĻĖ░ ņ£äĒĢ£ ņāüĒā£(State)ļŖö 1ņ░©ņøÉ (ĻĖ┤ĻĖē ņĀĢļ╣ä ņÜöĻĄ¼ ņłś)ņ£╝ļĪ£ ĻĄ¼ņä▒ĒĢśņśĆļŗż. Fig. 3ņØĆ ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äĒīĆ c1ņØ┤ 3ņØĖ Ļ▓ĮņÜ░ņÖĆ ļ»╝Ļ░ä ņĀĢļ╣äĒīĆ c2Ļ░Ć 2ņØĖ Ļ▓ĮņÜ░ņØ┤ļŗż. Fig. 3ņØĆ ļ»╝Ļ░ä ņĀĢļ╣äĒīĆņØ┤ ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņŚÉ ĒżĒĢ©ļÉśņ¢┤ ņ׳Ļ│Ā, ņä£ļ╣äņŖżļźĀņØ┤ ļÅÖņØ╝ĒĢśĻĖ░ ļĢīļ¼ĖņŚÉ ļ¬©ļŹĖ A ņØś Ļ▓ĮņÜ░ļŖö ņĀäņ▓┤ ņĀĢļ╣äĒīĆņØ┤ cĻ░Ć 5ņØĖ Ļ▓ĮņÜ░ņØś Impatient Ļ│ĀĻ░ØņØ┤ ņ׳ļŖö m/m/c ļ¬©ļŹĖĻ│╝ ļÅÖņØ╝ĒĢśĻ▓ī ļÉ£ļŗż.
ņāüĒā£ 0ņŚÉņä£ 1ļĪ£ņØś ņĀäņØ┤ļŖö ĻĖ┤ĻĖē ņĀĢļ╣ä ņÜöņ▓ŁļźĀņØ┤ ╬╗ļĪ£ ļ░£ņāØĒĢ£ ņāüĒā£ņØ┤Ļ│Ā, ņāüĒā£ 3ņŚÉņä£ 2ļĪ£ņØś ņĀäņØ┤ļŖö 3╬╝+3╬│ļĪ£ ļ░£ņāØĒĢśĻ▓ī ļÉ£ļŗż. ĻĘĖļ”¼Ļ│Ā ņāüĒā£ 5ņŚÉņä£ ĻĖ┤ĻĖē ņĀĢļ╣ä ņÜöņ▓ŁņØ┤ ļ░£ņāØĒĢśĻ▓ī ļÉśļ®┤ ĻĖ┤ĻĖē ņĀĢļ╣äņÜöņ▓ŁņØä ļ░øņØä ņłś ņŚåņ£╝ļ»ĆļĪ£ ņ░©ļŗ©(Blocking)ņØ┤ ļÉśņ¢┤ ĻĖ┤ĻĖēņĀĢļ╣äļź╝ ņŗżĒī©ĒĢśĻ▓ī ļÉ£ļŗż.
ĻĘĖļ”¼Ļ│Ā ņÜöņ▓ŁļÉ£ ĻĖ┤ĻĖē ņĀĢļ╣ä Ļ▒┤ņŚÉ ļīĆĒĢśņŚ¼ Ļ░ü ņāüĒā£ņŚÉņä£ ņĀĢļ╣äļź╝ ĒĢśļ®┤ņä£ ņÜöĻĄ¼ļÉ£ ņŗ£Ļ░äņŚÉ ņÖäļŻīĒĢśņ¦Ć ļ¬╗ĒĢśļ®┤ ņØ┤Ēāł(Reneging)ļÉśņ¢┤ ņŚŁņŗ£ ĻĖ┤ĻĖēņĀĢļ╣äļź╝ ņŗżĒī©ĒĢśĻ▓ī ļÉ£ļŗż. ņØ┤ļĢī iņØś ĻĖ┤ĻĖē ņĀĢļ╣äņÜöņ▓Ł Ļ▒┤ņØ┤ ņ׳ņØä ļĢī ĻĖ┤ĻĖē ņĀĢļ╣äļź╝ ņä▒Ļ│ĄĒĢĀ ĒÖĢļźĀņØä P i s P c s
ĒÖĢļźĀ ļ│Ćņłś Y1 ļ░Å Y2ļŖö ļŗ©Ļ│äĒśĢ ĒÖĢļźĀ ļ│Ćņłś Y1 Ōł╝ PH(Žä1, T1) ļ░Å Y2 Ōł╝ PH(Žä2, T2)ļĪ£ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż. Žä1, T1ņØĆ ņŗØ (8)Ļ│╝ Ļ░ÖņØ┤ Ēæ£ĒśäļÉ£ļŗż.
Žä2, T2ļŖö ĻĖ┤ĻĖē ņĀĢļ╣ä ņÜöņ▓ŁņØ┤ ļ░£ņāØĒ¢łņØä ļĢī, ņØ┤ļ»Ė ņÜöņ▓ŁļÉ£ ņĀĢļ╣äĻ▒┤ iņÖĆ cņŚÉ ļö░ļØ╝ ņāüņØ┤ĒĢśĻ▓ī ĻĄ¼ņä▒ļÉ£ļŗż. c = 5ņØ╝ ļĢī, i < 5ņØĖ Ļ▓ĮņÜ░ļŖö ņŗØ (9)ņÖĆ Ļ░Öļŗż.
ņŗØ (9)ļŖö ĻĖ┤ĻĖē ņĀĢļ╣äņÜöņ▓ŁņØ┤ ĻĖ┤ĻĖēņĀĢļ╣äĒīĆņØ┤ ņŚ¼ņ£ĀĻ░Ć ņ׳ņØä ļĢī ļ░£ņāØĒĢśņśĆņ£╝ļ»ĆļĪ£ ļīĆĻĖ░ ņŗ£Ļ░ä ņŚåņØ┤ ņĀĢļ╣äļź╝ ļ░øņØä ņłś ņ׳ļŖö Ļ▓āņØä ņØśļ»ĖĒĢ£ļŗż.
i = 5ņØĖ Ļ▓ĮņÜ░ļŖö ņŗØ (10)Ļ│╝ Ļ░Öļŗż.
ņŗØ (10)ļŖö ņĀĢļ╣äĻ▒┤ņłśĻ░Ć 5ņØĖ ĻĖ┤ĻĖē ņĀĢļ╣äņÜöņ▓ŁņØ┤ ļ░£ņāØĒĢĀ Ļ▓ĮņÜ░ ļ░öļĪ£ ņĀĢļ╣äļź╝ ļ░øņ¦Ć ļ¬╗ĒĢśĻ│Ā 5╬╝+5╬│ļ¦īĒü╝ ļīĆĻĖ░ Ēøä ņĀĢļ╣äļź╝ ļ░øĻ▓ī ļÉśļŖö Ļ▓āņØä ņØśļ»ĖĒĢ£ļŗż.
3.2.2 ļ¬©ļŹĖ B: ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣ä ņØĖļĀź ņÜ░ņäĀ ņĀĢļ╣ä ļ¬©ĒśĢ
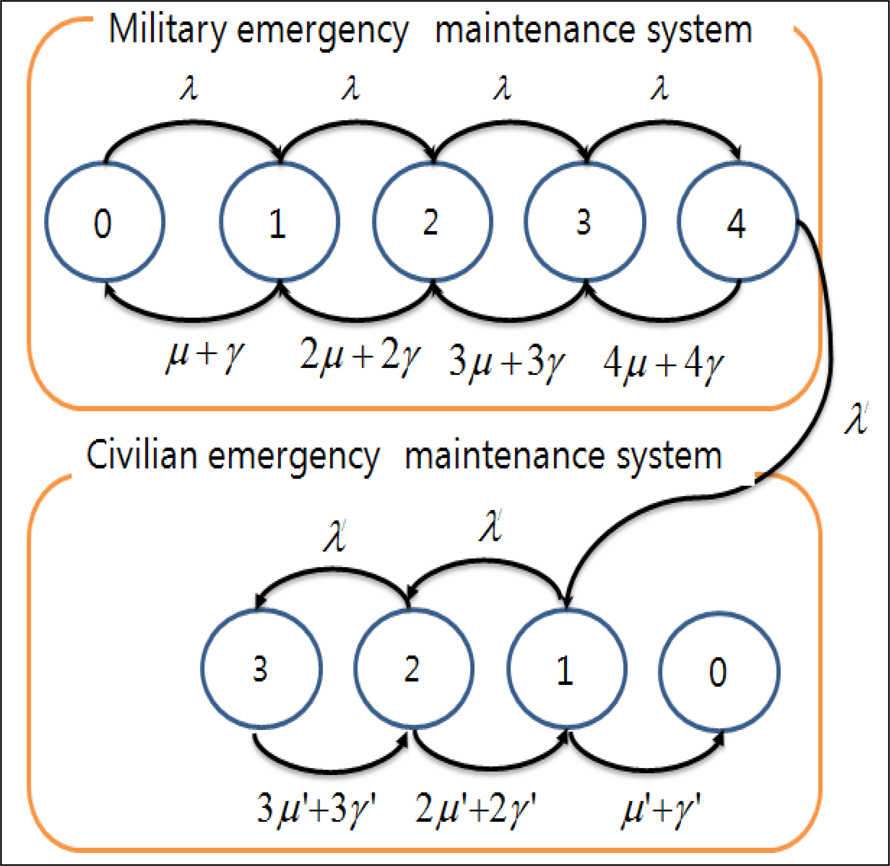
ļ¬©ļŹĖ B ņŗ£ņØś ĻĖ┤ĻĖēņĀĢļ╣äĒīĆ ņÜ┤ņÜ®ņØĆ Fig. 4ņÖĆ Ļ░ÖņØ┤ Ēæ£ĒśäĒĢĀ ņłś ņ׳ļŗż.
ņ×æņĀä ņĀäļĀźņŚÉņä£ ĒżņĢäņåĪ Ļ│╝ņĀĢņ£╝ļĪ£ ņןļ╣äĻ│Āņן(╬╗)ņØ┤ ļ░£ņāØĒĢśļ®┤ ĻĄ░ ņĀĢļ╣äĒīĆĻ│╝ ļ»╝Ļ░ä ņĀĢļ╣äĒīĆņØ┤ ĒśæņŚģĒĢśņŚ¼ ņ¦ĆņłśļČäĒż(╬╝)ļĪ£ ņĀĢļ╣äļź╝ ņŗżņŗ£ĒĢśĻ▓ī ļÉśĻ│Ā ņĀĢļ╣äļź╝ ņÖäļŻīĒĢ┤ņĢ╝ ļÉśļŖö ņŗ£Ļ░äņØĆ ╬│ņØś ņØ┤Ēāłņ£©ņØä Ļ░Ćņ¦ĆļŖö ņ¦ĆņłśļČäĒżļź╝ ļö░ļź┤Ļ▓ī ļÉ£ļŗż. ĒżņĢäņåĪ Ļ│╝ņĀĢņØś ņןļ╣äĻ│ĀņןņØ┤ ļ░£ņāØĒĢśļ®┤ ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äĒīĆņØ┤ ņ¦ĆņłśļČäĒż(╬╝)ļĪ£ ņÜ░ņäĀ ņĀĢļ╣äļź╝ ņŗżņŗ£ĒĢśĻ│Ā, ĻĖ┤ĻĖē ņĀĢļ╣äļź╝ ņŗżĒī©ĒĢ£ Ļ▓ĮņÜ░ ļ»╝Ļ░ä ĻĖ┤ĻĖēņĀĢļ╣äĒīĆņ£╝ļĪ£ ņĀäļŗ¼ļÉśĻĖ░ ļĢīļ¼ĖņŚÉ ļ»╝Ļ░ä ĻĖ┤ĻĖēņĀĢļ╣äĒīĆņØ┤ ļŗ┤ļŗ╣ĒĢ┤ņĢ╝ ļÉĀ ņĀĢļ╣äņÜöņ▓ŁļźĀ, ņÖäļŻīĒĢ┤ņĢ╝ ļÉśļŖö ņŗ£Ļ░äņØ┤ ļŗ¼ļØ╝ņ¦ĆĻ▓ī ļÉ£ļŗż. ņ”ē ņØ┤Ēāł, ņ░©ļŗ© ļō▒ņ£╝ļĪ£ ņĀĢļ╣äļź╝ ņŗżĒī©ĒĢ£ ĒÖĢļźĀļČäĒżļĪ£ ņĀĢļ╣äņÜöņ▓ŁļźĀņØ┤ ļ░£ņāØĒĢśĻ▓ī ļÉ£ļŗż. ņØ┤ļĢīņØś ņĀĢļ╣äņÜöņ▓ŁļźĀņØĆ ņŗØ (6)ņØä ĒåĄĒĢśņŚ¼ ļÅäņČ£ĒĢĀ ņłś ņ׳ļŗż.
ņĀäņØ┤ņ£©Ē¢ēļĀ¼ņØä ĻĄ¼ņä▒ĒĢśĻĖ░ ņ£äĒĢ£ ļ¬©ļŹĖ AņÖĆ ļÅÖņØ╝ĒĢśĻ▓ī ņāüĒā£(State)ļŖö 1ņ░©ņøÉ (ĻĖ┤ĻĖē ņĀĢļ╣ä ņÜöĻĄ¼ ņłś) ņ£╝ļĪ£ ĻĄ¼ņä▒ĒĢśņśĆļŗż. Fig. 5ļŖö ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äĒīĆ c1ņØ┤ 4ņØĖ Ļ▓ĮņÜ░ņÖĆ ļ»╝Ļ░ä ņĀĢļ╣äĒīĆņØ┤ c2ņØ┤ 3ņØĖ Ļ▓ĮņÜ░ņØ┤ļŗż. ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņÖĆ ļ»╝Ļ░ä ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äĻ░Ć Ļ░üĻ░üņØś ņĀĢļ╣äĒīĆņ£╝ļĪ£ ņ£╝ļĪ£ ņÜ┤ņśüļÉśļŖö Ļ▓āņØä ņĢī ņłś ņ׳ļŗż.
ĻĄ░ ļ░Å ļ»╝Ļ░ä ĻĖ┤ĻĖēņĀĢļ╣äņŗ£ņŖżĒģ£ņŚÉ iņØś ĻĖ┤ĻĖē ņĀĢļ╣äņÜöņ▓Ł Ļ▒┤ņØ┤ ņ׳ņØä ļĢī ĻĖ┤ĻĖē ņĀĢļ╣äļź╝ ņä▒Ļ│ĄĒĢĀ ĒÖĢļźĀņØä Ļ░üĻ░ü P j ms P j cs P c 1 m s P c 2 c s
Ļ░ü ņĀĢļ╣äņŗ£ņŖżĒģ£ņŚÉņä£ iņØś ĻĖ┤ĻĖē ņĀĢļ╣äņÜöņ▓Ł Ļ▒┤ņØ┤ ņ׳ņØä ļĢī ņĀĢļ╣äņÜöĻĄ¼ĻĖ░Ļ░ä ņØ┤ļé┤ņŚÉ ņĀĢļ╣äļź╝ ļ░øņ¦Ć ļ¬╗ĒĢĀ ĒÖĢļźĀ(Reneging Probability)ļŖö ņŗØ (7) Ōł╝ (9)ļź╝ ĒåĄĒĢśņŚ¼ ņé░ņČ£ĒĢĀ ņłś ņ׳ļŗż. ĻĘĖļ”¼Ļ│Ā iĻ▒┤ņØś ņĀĢļ╣äņÜöņ▓Ł Ļ▒┤ņłśĻ░Ć ņ׳ņØä ļĢī ĻĄ░ ļ░Å ļ»╝Ļ░äņØś ĻĖ┤ĻĖēņĀĢļ╣äņŗ£ņŖżĒģ£ņØ┤ ĻĖ┤ĻĖēņĀĢļ╣äļź╝ ņä▒Ļ│ĄĒĢĀ ĒÖĢļźĀņØĖ P c 1 m s P c 2 c s
ņŗØ (12)ļŖö ĻĄ░ ļ░Å ļ»╝Ļ░ä ĻĖ┤ĻĖēņĀĢļ╣äņŗ£ņŖżĒģ£ ļ¬©ļæÉ ĻĖ┤ĻĖēņĀĢļ╣äļź╝ ņŗżĒī©ĒĢĀ ĒÖĢļźĀņŚÉņä£ 1ņØä ļ║Ć Ļ░ÆņØ┤ ņĀäņ▓┤ ĻĖ┤ĻĖē ņĀĢļ╣äņØś ņä▒Ļ│ĄĒÖĢļźĀņØ┤ ļÉ£ļŗżļŖö ņØśļ»ĖņØ┤ļŗż.
ņłśņ╣śņŗżĒŚś ļ░Å Ļ▓░Ļ│╝ļČäņäØ
4.1. ņŗżĒŚśņĪ░Ļ▒┤
ļ│Ė ņŚ░ĻĄ¼ņØś ņŗżĒŚśņŚÉņä£ļŖö Matlab 2014aļź╝ ĒÖ£ņÜ®ĒĢśņŚ¼ ļČäņäØ ĒĢśņśĆņ£╝ļ®░, ņŻ╝ņÜö ņłśņ╣śļŖö ņØśļ»Ė ņ׳ļŖö Ļ▓░Ļ│╝ ļÅäņČ£ņØä ņ£äĒĢ┤ ĻĖ┤ĻĖē ņĀĢļ╣äĒŖ╣ņ¦ĢņØä ņĄ£ļīĆĒĢ£ Ļ│ĀļĀżĒĢ£ ļ¬©ņłś Ļ░ÆņØä ņé¼ņÜ®Ē¢łļŗż.
4.2 ļ¬©ļŹĖ A ļČäņäØĻ▓░Ļ│╝
Table 1ņØĆ ņ×æņĀä ņÜ┤ņÜ® ņżæ ĻĖ┤ĻĖē ņĀĢļ╣ä ļ░£ņāØļźĀ ╬╗ = 2, ņä£ļ╣äņŖżņ£© ╬╝ = 0.5, ņĀĢļ╣ä ņÖäļŻī ņÜöĻĄ¼ļźĀņØä ╬│ = 0.12ņ£╝ļĪ£ ņäżņĀĢĒĢśņŚ¼ ĻĖ┤ĻĖē ņĀĢļ╣äĒīĆņØś ļ│ĆĒÖöņŚÉ ļö░ļźĖ ĻĖ┤ĻĖē ņĀĢļ╣ä ņä▒Ļ│ĄĒÖĢļźĀņØä ļČäņäØĒĢ£ Ļ▓āņØ┤ļŗż. ĻĖ┤ĻĖē ņĀĢļ╣äĒīĆņØś ņłśņżĆ ņ”ØĻ░ĆņŚÉ ļö░ļØ╝ ĻĖ┤ĻĖē ņĀĢļ╣ä ņä▒Ļ│Ą ĒÖĢļźĀņØ┤ ņĢłņĀĢĒÖö(Stable)ļÉ©ņØä ņĢī ņłś ņ׳ļŗż. ņØ┤ļŖö ņ░©ļŗ©ĒÖĢļźĀņØĆ ņĀĢļ╣äĒīĆņØ┤ ņ”ØĻ░ĆĒĢĀņłśļĪØ ņ░©ļŗ©ĒÖĢļźĀņØĆ ņżäņ¢┤ļōżĻ▓ī ļÉśņ¦Ćļ¦ī ņØ┤Ēāł ĒÖĢļźĀņØś Ļ░ÉņåīĒÅŁņØĆ ņä£ļ╣äņŖżņ£©Ļ│╝ ņĀĢļ╣ä ņÖäļŻī ņÜöĻĄ¼ļźĀņŚÉ ĻĖ░ņØĖĒĢśņŚ¼ ļ░£ņāØĒĢśĻĖ░ ļĢīļ¼ĖņØ┤ļŗż. ĻĘĖļ”¼Ļ│Ā ņØ┤Ēāł ĒÖĢļźĀņØĆ ņĀĢļ╣äĒīĆņØś ņłśņżĆ ņ”ØĻ░ĆņŚÉ ļö░ļØ╝ ļ░£ņāØĒÅŁņØ┤ ļ»Ėļ»ĖĒĢśĻ▓ī ņ”ØĻ░ĆĒĢśĻ▓ī ļÉśļŖö ļŹ░ ņØ┤ļŖö ņ░©ļŗ©ĒÖĢļźĀņØ┤ ņżäņ¢┤ļō¼ņŚÉ ļö░ļØ╝ ņŗ£ņŖżĒģ£ņØś ņĀĢļ╣ä ņłśĒ¢ēņØ┤ ņ”ØĻ░ĆĒĢśĻ│Ā ņĀĢļ╣ä ņÖäļŻī ņÜöĻĄ¼ņŗ£Ļ░äņØĆ Ļ░ü ņĀĢļ╣äĒīĆņØś ņä£ļ╣äņŖżņ£©ņŚÉ ļ¦ÄņØĆ ņśüĒ¢źņØä ļ░øĻĖ░ ļĢīļ¼ĖņØ┤ļŗż.
Table┬Ā1.
Success probability of emergency maintenance according to server change
Table 1ņØś Ļ▓░Ļ│╝ļź╝ ļ░öĒāĢņ£╝ļĪ£ ĻĄ░ ņØśņé¼Ļ▓░ņĀĢĻČīņ×ÉļŖö ļ¬®Ēæ£ ņĀĢļ╣äĒÖĢļźĀņŚÉ ļö░ļØ╝ ĻĖ┤ĻĖē ņĀĢļ╣äĒīĆ ņłśļź╝ Ļ▓░ņĀĢĒĢĀ ņłś ņ׳ņØä Ļ▓āņØ┤ļ®░, ņØ┤ ņżæ ĻĄ░ ĻĖ┤ĻĖē ņĀĢļ╣äĒīĆņØś ņłśļź╝ Ļ│ĀļĀżĒĢśņŚ¼ ļ»╝Ļ░ä ĻĖ┤ĻĖē ņĀĢļ╣äĒīĆņØś ņłśļź╝ Ļ▓░ņĀĢĒĢĀ ņłś ņ׳ņØä Ļ▓āņØ┤ļŗż. ņśłļĪ£ ļ¬®Ēæ£ ĻĖ┤ĻĖē ņĀĢļ╣äņä▒Ļ│ĄļźĀņØä 60 %ļĪ£ ņäżņĀĢĒĢśĻ│Ā Ēśäņ×¼ ņĀĢļ╣äĒīĆņØś ņłśĻ░Ć 4ļĪ£ Ļ▓░ņĀĢļÉśņ¢┤ ņ׳ļŗżļ®┤ ļ»╝Ļ░ä ņĀĢļ╣äĒīĆņØś ņłśļŖö 4ļĪ£ ĒĢśļŖö Ļ▓āņØ┤ ņĄ£ņĀüņØ╝ Ļ▓āņØ┤ļŗż.
4.3 ļ¬©ļŹĖ B ļČäņäØĻ▓░Ļ│╝
ļ¬©ļŹĖ BņØś ĻĄ░ ņĀĢļ╣äņŗ£ņŖżĒģ£ņØś ļ¬©ņłś Ļ░ÆņØĆ ļČäņäØ Ļ░ÆņØś ņØ┤ĒĢ┤ļź╝ ļÅĢĻĖ░ ņ£äĒĢ┤ ļ¬©ļŹĖ AņØś ļ¬©ņłś Ļ░ÆņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļČäņäØĒĢśņśĆĻ│Ā Ļ▓░Ļ│╝ļŖö Table 1Ļ│╝ ļÅÖņØ╝ĒĢśļŗż. Table 2ļŖö ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äņŗ£ņŖżĒģ£ņŚÉņä£ ņØ┤Ēāł ļ░Å ņ░©ļŗ©ļÉ£ ņĀĢļ╣äĻ▒┤ņŚÉ ļīĆĒĢśņŚ¼ ļ»╝Ļ░ä ņĀĢļ╣äņŗ£ņŖżĒģ£ņŚÉņä£ ņä£ļ╣äņŖżĒĢśļŖö ĒŖ╣ņä▒ņØä Ļ│ĀļĀżĒĢśņŚ¼ ņ×æņĀä ņÜ┤ņÜ® ņżæ ĻĖ┤ĻĖē ņĀĢļ╣ä ļ░£ņāØļźĀ ╬╗ŌĆ▓ = 1.44, ņä£ļ╣äņŖżņ£© ╬╝ = 0.1, ņĀĢļ╣ä ņÖäļŻī ņÜöĻĄ¼ļźĀņØä ╬│= 0.33ņ£╝ļĪ£ ņäżņĀĢĒĢśņŚ¼ ĻĖ┤ĻĖē ņĀĢļ╣äĒīĆņØś ļ│ĆĒÖöņŚÉ ļö░ļźĖ ĻĖ┤ĻĖē ņĀĢļ╣ä ņä▒Ļ│ĄĒÖĢļźĀņØä ļČäņäØĒĢ£ Ļ▓āņØ┤ļŗż. ņä£ļ▓äņØś ņłśĻ░Ć ņ”ØĻ░ĆĒĢĀņłśļĪØ ņĢĮ 23 %ņØś ņĢłņĀĢĒÖĢĒā£ ĒÖĢļźĀņØä Ļ░¢ļŖö Ļ▓āņØä ņĢī ņłś ņ׳ļŗż.
Table┬Ā2.
Success probability of civilian emergency maintenance according to server change
ņ£äņØś ļÅäņČ£ļÉ£ Ļ▓░Ļ│╝ņÖĆ ņŗØ (12)ņØä ļ░öĒāĢņ£╝ļĪ£ ļČäņäØĒĢ£ ļ¬©ļŹĖ BņØś ņĀĢļ╣äņä▒Ļ│ĄĒÖĢļźĀ Ļ▓░Ļ│╝ļŖö Table 3Ļ│╝ Ļ░Öļŗż. Table 3Ļ│╝ ļÅÖņØ╝ĒĢ£ ļ░®ņŗØņ£╝ļĪ£ ĻĄ░Ļ│╝ ļ»╝Ļ░ä ĻĖ┤ĻĖēņĀĢļ╣äĒīĆņØś ņłśļź╝ ņ×ÉļŻīļź╝ ļ░öĒāĢņ£╝ļĪ£ ļŗżņ¢æĒĢ£ ļČäņäØņØ┤ Ļ░ĆļŖźĒĢĀ Ļ▓āņØ┤ļŗż.
Table┬Ā3.
Success probability of model A(c1 = 6)
| # of Server | # of civilian Server | Success Probability |
|---|---|---|
| 6 | 3 | 0.5200 |
| 4 | 0.5784 | |
| 5 | 0.6002 | |
| 6 | 0.6139 | |
| 7 | 0.6183 |
Table 3ņØś Ļ▓░Ļ│╝ļź╝ ļ░öĒāĢņ£╝ļĪ£ ĻĄ░ ņØśņé¼Ļ▓░ņĀĢĻČīņ×ÉļŖö ļ¬®Ēæ£ ņĀĢļ╣äņä▒Ļ│ĄĒÖĢļźĀņØä ĻĖ░ņżĆņ£╝ļĪ£ ļ»╝Ļ░ä ĻĖ┤ĻĖēņĀĢļ╣äĒīĆņØś ņłśļź╝ Ļ▓░ņĀĢĒĢĀ ņłś ņ׳ņØä Ļ▓āņØ┤ļŗż. ļ¦īņĢĮ ĻĄ░ ĻĖ┤ĻĖēņĀĢļ╣äĒīĆņØś ņłśĻ░Ć 6, ļ¬®Ēæ£ ņĀĢļ╣äņä▒Ļ│ĄĒÖĢļźĀņØ┤ 60 %ļØ╝Ļ│Ā ņäżņĀĢĒĢ£ļŗżļ®┤ ņĄ£ņĀü ļ»╝Ļ░ä ĻĖ┤ĻĖē ņĀĢļ╣äĒīĆņØś ņłśļŖö 5Ļ░Ć ļÉĀ Ļ▓āņØ┤ļŗż.
Ļ▓░ ļĪĀ
ļ│Ė ņŚ░ĻĄ¼ņŚÉņä£ļŖö Impatience ĒŖ╣ņä▒ņØ┤ ĒāĆ ļČäņĢ╝ņŚÉ ļ╣äĒĢ┤ ņāüļīĆņĀüņ£╝ļĪ£ ņŗ£Ļ░äņŚÉ ĻĄŁļ░®ļČäņĢ╝ņŚÉ ņżæņÜöĒĢśĻ│Ā, ĒŖ╣Ē׳ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņŚÉ ļ»╝Ļ░ä ņØĖļĀźĻ│╝ņØś ĒśæņŚģņØ┤ ņ”ØļīĆļÉśļŖö ņāüĒÖ®ņØä Ļ│ĀļĀżĒĢśņŚ¼ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņØś ĻĄ░ ļ░Å ļ»╝Ļ░ä ņĀĢļ╣äņØĖļĀźņØś ņĀüņĀĢ ĻĘ£ļ¬©, ĒÄĖņä▒ Ļ▓░ņĀĢņØä ņ£äĒĢ£ ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņØś ņä▒ļŖźļČäņäØ ļ¬©ļŹĖņØä ņĀ£ņŗ£ĒĢśņśĆĻ│Ā ņłśņ╣śļČäņäØņØä ĒåĄĒĢśņŚ¼ ĻĄ░Ļ│╝ ļ»╝Ļ░ä ĻĖ┤ĻĖēņĀĢļ╣äĒīĆņØś ņĀüņĀĢ ĻĘ£ļ¬©ļź╝ ļČäņäØĒĢśņśĆļŗż. ņØ┤ļ¤¼ĒĢ£ ņŚ░ĻĄ¼ļŖö ĻĄ░ ņØśņé¼Ļ▓░ņĀĢĻČīņ×ÉņŚÉĻ▓ī ĻĖ┤ĻĖēņĀĢļ╣äņ▓┤Ļ│äņØś ļ¬®Ēæ£ņä▒ļŖźņØä ļ¦īņĪ▒ĒĢĀ ņłś ņ׳ļŖö ĻĄ░Ļ│╝ ļ»╝Ļ░ä ņØĖļĀźņØś ņĀüņĀĢ ĻĘ£ļ¬© ņé░ņĀĢņØä ĒåĄĒĢśņŚ¼ ņ×æņĀäņĀäļĀźņØś ņĀäļ╣äĒā£ņäĖ(Readiness) Ē¢źņāüņØĆ ļ¼╝ļĪĀ ĻĄ░ ņĀĢļ╣äņśłņé░ņØä ĒÜ©ņ£©ņĀüņ£╝ļĪ£ ņé¼ņÜ®ĒĢśĻĖ░ ņ£äĒĢ£ ņżæņÜöĒĢ£ ņĀĢļ│┤ļź╝ ņĀ£Ļ│ĄĒĢĀ ņłś ņ׳ļŗżļŖö ņĀÉņŚÉņä£ ļ│Ė ņŚ░ĻĄ¼ņØś ņØśņØśĻ░Ć ņ׳ļŗż.