|
 |
- Search
| J. KIMS Technol > Volume 24(4); 2021 > Article |
|
Abstracts
This study describes the depth and straight motion control performance depending on control surface combinations of a supercavitating underwater vehicle. When an underwater vehicle experiences supercavitation, friction resistance can be minimized, thus achieving the effect of super-high-speed driving. Six degrees of freedom modeling of the underwater vehicle are performed and the guidance and control loops are designed with not only a cavitator and an elevator, but also a rudder and a differential elevator to improve the stability of the roll and yaw axis. The control performance based on the combination of control surfaces is analyzed by the root-mean-square error for keeping depth and straight motion.
мҙҲкіөлҸҷ(supercavitation)мқҙлһҖ нҠ№м • мҳЁлҸ„м—җм„ң м••л Ҙмқ„ лӮ®м¶ӨмңјлЎңмҚЁ м•ЎмІҙк°Җ кё°мІҙлЎң кё°нҷ”лҗң лІ„лё”лЎң кө¬м„ұлҗң кіөлҸҷмқҙ мҲҳмӨ‘мҡҙлҸҷмІҙ м „мІҙлҘј к°җмӢёлҠ” нҳ„мғҒмқ„ мқҳлҜён•ңлӢӨ. мқҙлҹ¬н•ң мҙҲкіөлҸҷ нҳ„мғҒмқ„ мқҙмҡ©н• кІҪмҡ° мЈјн–ү н•ӯл Ҙмқҳ лҢҖл¶Җ분мқ„ м°Ём§Җн•ҳлҠ” л§Ҳм°°м Җн•ӯмқ„ мөңмҶҢнҷ”н• мҲҳ мһҲм–ҙ мҙҲкі мҶҚ мЈјн–үмқҙлқјлҠ” нҡЁкіјлҘј м–»мқ„ мҲҳ мһҲлӢӨ[1вҖ“4]. мөңк·ј м„ м§„көӯл“Өмқ„ мӨ‘мӢ¬мңјлЎң кҙҖл Ё кё°мҲ мқҙ мһ¬мЎ°лӘ…лҗҳкі мһҲмңјл©°, мҙҲкіөлҸҷ мҲҳмӨ‘мҡҙлҸҷмІҙлҠ” лҹ¬мӢңм•„мҷҖ лҸ…мқјм—җм„ң к°ңл°ңлҗҳм—Ҳкі лҜёкөӯкіј мӨ‘көӯм—җм„ңлҸ„ к°ңл°ң мӨ‘мқё кІғмңјлЎң м•Ңл Өм ё мһҲлӢӨ. мҳҲлҘј л“Өм–ҙ 1960л…„лҢҖ кө¬мҶҢл Ём—җм„ң к°ңл°ңлҗң мҙҲкіөлҸҷ м–ҙлў° VA-111 ShkvalмқҖ 1977л…„кІҪл¶Җн„° мҡҙмҡ©лҗҳкі мһҲлӢӨ. лҜёкөӯмқҳ Juliet Marine Systems зӨҫлҠ” мҙҲкіөлҸҷ л°ңмғқ мҲҳмӨ‘ 추진л¶ҖлҘј мқҙмҡ©н•ң GHOST мҙҲкіөлҸҷ н•Ём •мқ„ 비лЎҜн•ҳм—¬ мҙҲкіөлҸҷ мһ мҲҳн•Ёмқҳ к°ңл°ңмқ„ кі„нҡҚн•ҳкі мһҲмңјл©°, л…ёлҘҙмӣЁмқҙ DSG зӨҫлҠ” мҙҲкіөлҸҷ нҳ„мғҒмқ„ мқҙмҡ©н•ң нғ„м•Ҫмқ„ к°ңл°ңн•ҳмҳҖлӢӨ.
кё°мЎҙм—җлҠ” мҙҲкіөлҸҷ мҲҳмӨ‘мҡҙлҸҷмІҙмқҳ 추진мӢңмҠӨн…ңкіј мң мІҙм—ӯн•ҷм Ғ м—°кө¬[5вҖ“8]м—җ мҙҲм җмқҙ л§һм¶°м ё мһҲм—ҲлӢӨл©ҙ, мөңк·јм—җлҠ” мҙҲкі мҶҚм—җм„ңмқҳ м•Ҳм •м„ұкіј мЈјн–үм„ұмқ„ 분м„қн•ҳкё° мң„н•ң лҸҷм—ӯн•ҷ лӘЁлҚёл§Ғ л°Ҹ м ңм–ҙ м—°кө¬к°Җ нҷңл°ңнһҲ мқҙлЈЁм–ҙм§Җкі мһҲлӢӨ[1вҖ“4]. Kim & Kim[1вҖ“3]мқҖ мў…л°©н–Ҙмқҳ к°ңлЈЁн”„ м„ұлҠҘ 분м„қ л°Ҹ мў…л°©н–Ҙм—җм„ңмқҳ мһҗм„ём ңм–ҙмҷҖ мӢ¬лҸ„м ңм–ҙ л°Ҹ мҡҙн•ӯмҳҒм—ӯ ліҙнҳём—җ кҙҖн•ң м—°кө¬кІ°кіјлҘј м ңмӢңн•ҳмҳҖлӢӨ. м°ёкі л¬ён—Ң[4]лҠ” нҡЎл°©н–Ҙм—җм„ңмқҳ к°ңлЈЁн”„ м„ұлҠҘм—җ кҙҖн•ң м—°кө¬кІ°кіјлҘј м ңмӢңн•ҳмҳҖмңјлӮҳ м§Ғ진м ңм–ҙлҘј мң„н•ң нҡЎм¶•/л°©н–Ҙ축 нҸҗлЈЁн”„ м ңм–ҙм—җ кҙҖн•ң м„ұлҠҘмқ„ м ңмӢңн•ҳм§Җ м•Ҡм•ҳлӢӨ. мқҙлҹ¬н•ң л°°кІҪмңјлЎң кі мҶҚ мғҒнғңм—җм„ңмқҳ нҡЎл°©н–Ҙкіј л°©н–Ҙ축 нҠ№м„ұмқ„ кі л Өн•ң м§Ғ진 л°Ҹ мӢ¬лҸ„ м ңм–ҙм—җ кҙҖн•ң м—°кө¬лҠ” лҜёл№„н•ң мӢӨм •мқҙл©°, мЎ°мў…л©ҙмңјлЎң нҷңмҡ© к°ҖлҠҘн•ң м „л°©мқҳ мәҗ비н…Ңмқҙн„°мҷҖ нӣ„л°©мқҳ м—ҳлҰ¬лІ мқҙн„°/лҹ¬лҚ”лҘј м–ҙл– н•ң мЎ°н•©мңјлЎң нҷңмҡ©н• кІғмқёк°Җм—җ лҢҖн•ң 분м„қмқҙ н•„мҡ”н•ҳлӢӨ.
мў…л°©н–Ҙмқҳ кІҪмҡ° н”јм№ҳк°Ғ л°Ҹ мӢ¬лҸ„м ңм–ҙлҘј мң„н•ҳм—¬ мәҗ비н…Ңмқҙн„°мҷҖ м—ҳлҰ¬лІ мқҙн„°мқҳ лҸҷмӢң нҷңмҡ©мқҙ к°ҖлҠҘн•ҳл©°, м§Ғ진м„ұлҠҘ н–ҘмғҒмқ„ мң„н•ҳм—¬ нӣ„л°©мқҳ лҹ¬лҚ”лҘј мқҙмҡ©н•ң л°©н–Ҙ축 м ңм–ҙлҘј кі л Өн• мҲҳ мһҲлӢӨ. нҠ№нһҲ, нӣ„л°©м—җ мһҘм°©лҗҳлҠ” мўҢмҡ° м—ҳлҰ¬лІ мқҙн„° н•ҖмқҖ мў…л°©н–Ҙ м ңм–ҙлҘј мң„н•ҳм—¬ лҸҷкё°нҷ”лҗң мҡҙмҡ©мқҙ к°ҖлҠҘн• лҝҗ м•„лӢҲлқј, мўҢмҡ° м—ҳлҰ¬лІ мқҙн„°лҘј н•ӯкіөкё°мқҳ м—җмқјлҹ¬лЎ кіј мң мӮ¬н•ҳкІҢ м°Ёл“ұ мЎ°мў…л©ҙ(differential control surface)мңјлЎң нҷңмҡ©н•ҳм—¬ нҡЎл°©н–Ҙ м ңм–ҙм—җ м Ғмҡ©н• мҲҳ мһҲлӢӨ. ліё м—°кө¬м—җм„ңлҠ” мқҙлҹ¬н•ң лӢӨм–‘н•ң мЎ°мў…л©ҙ мЎ°н•©м—җ л”°лҘё мҙҲкіөлҸҷ мҲҳмӨ‘мҡҙлҸҷмІҙмқҳ мӢ¬лҸ„ л°Ҹ м§Ғ진 м ңм–ҙмқҳ м„ұлҠҘмқ„ 분м„қн•ҳмҳҖмңјл©°, мҲҳм№ҳ мӢң뮬л Ҳмқҙм…ҳмқ„ нҶөн•ҳм—¬ кіөлҸҷмқҙ нҳ•м„ұлҗҳлҠ” мҙҲкё°мқҳ л¶Ҳм•Ҳм •н•ң кө¬к°„м—җм„ң мЎ°мў…л©ҙ мЎ°н•©мқ„ нҶөн•ң нҡЎм¶•кіј л°©н–Ҙ축 м ңм–ҙлҘј нҶөн•ҙ м§Ғ진м„ұлҠҘмқҙ н–ҘмғҒлҗ мҲҳ мһҲмқҢмқ„ нҷ•мқён•ҳмҳҖлӢӨ.
2мһҘм—җм„ңлҠ” мҙҲкіөлҸҷ мҲҳмӨ‘мҡҙлҸҷмІҙмқҳ 6мһҗмң лҸ„ лӘЁлҚёл§Ғмқ„ мқҙмҡ©н•ң мӢң뮬л Ҳмқҙм…ҳ нҷҳкІҪ кө¬м¶•мқ„ кё°мҲ н•ҳмҳҖкі , 3мһҘм—җм„ңлҠ” м§Ғ진주н–ү л°Ҹ мӢ¬лҸ„ м ңм–ҙлҘј мң„н•ң м ңм–ҙлІ•м№ҷ м„Өкі„лҘј кё°мҲ н•ҳмҳҖлӢӨ. лҳҗн•ң, 4мһҘм—җм„ңлҠ” мҲҳм№ҳ мӢң뮬л Ҳмқҙм…ҳмқ„ нҶөн•ң м•Ҳм •м„ұ л°Ҹ мЎ°мў…л©ҙ мЎ°н•©м—җ л”°лҘё мЈјн–үм„ұлҠҘмқ„ 분м„қн•ҳмҳҖкі 5мһҘм—җм„ңлҠ” кІ°лЎ мҲңмңјлЎң лӮҳм—ҙн•ҳмҳҖлӢӨ.
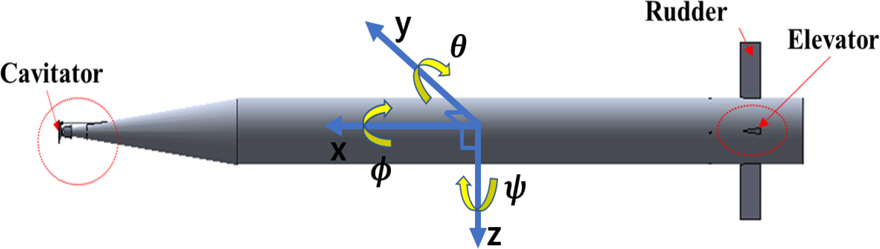
мҙҲкіөлҸҷ мҲҳмӨ‘мҡҙлҸҷмІҙмқҳ нҳ•мғҒмқҖ Fig. 1кіј к°ҷкі лҸҷм—ӯн•ҷ лӘЁлҚёл§ҒмқҖ MATLAB/Simulink нҷҳкІҪм—җм„ң мҲҳн–үлҗҳл©°, лҸҷм—ӯн•ҷ лӘЁлҚёмқҖ кіөлҸҷ, мәҗ비н…Ңмқҙн„°, н•Җ, мң мІҙл Ҙ лӘЁлҚёл§Ғ л“ұмңјлЎң кө¬м„ұлҗңлӢӨ.
мҲҳмӨ‘мҡҙлҸҷмІҙмқҳ 6мһҗмң лҸ„ мҡҙлҸҷл°©м •мӢқмқҖ мӢқ (1)кіј (2)лЎң н‘ңнҳ„лҗҳл©°, мһ‘мҡ©н•ҳлҠ” нһҳкіј лӘЁл©ҳнҠёлҠ” мјҖ비н…Ңмқҙн„°, н•Җ, мң мІҙл Ҙ л“ұмңјлЎң лӮҳлҲ„м–ҙ кі л ӨлҗңлӢӨ.
м—¬кё°м„ң, ()Thrust, ()Cavitator, ()Fins, ()Gravity, ()Wet, ()planing лҠ” к°Ғк°Ғ 추л Ҙ, мјҖ비н…Ңмқҙн„°, н•Җ, мӨ‘л Ҙ, мң мІҙл Ҙл°Ҹ н”Ңл ҲмқҙлӢқм—җ мқҳн•ң нһҳкіј лӘЁл©ҳнҠёлҘј мқҳлҜён•ңлӢӨ.
лҳҗн•ң, мҳӨмқјлҹ¬к°Ғмқ„ кі„мӮ°н•ҳкё° мң„н•ң мҲҳмӨ‘мҡҙлҸҷмІҙмқҳ мҡҙлҸҷм—ӯн•ҷ л°©м •мӢқмқҖ мӢқ (3)кіј к°ҷлӢӨ.
кіөлҸҷ лӘЁлҚёл§Ғм—җм„ң мӨ‘мҡ”н•ң нҢҢлқјлҜён„°лҠ” кіөлҸҷмҲҳ(Пғc)мқҙл©° мқјл°ҳм ҒмңјлЎң мӢқ (4)мҷҖ к°ҷмқҙ н‘ңнҳ„лҗңлӢӨ.
м—¬кё°м„ң pвҲһмҷҖ pcлҠ” лҸҷмқј мҲҳмӢ¬м—җм„ң к°–лҠ” мң мІҙмқҳ м •м••кіј кіөлҸҷ лӮҙ м••л ҘмқҙлӢӨ. ліё м—°кө¬м—җм„ңлҠ” мәҗ비н…Ңмқҙн„° л¶Җк·јм—җ к°ҖмҠӨмҷҖ кіөкё°лҘј мқёмң„м ҒмңјлЎң мЈјмһ…н•ҳм—¬ кіөлҸҷмқ„ нҳ•м„ұн•ҳмҳҖкі , 비көҗм Ғ м ҖмҶҚм—җм„ңлҸ„ мӢ мҶҚн•ҳкІҢ кіөлҸҷмқҙ нҳ•м„ұлҗҳлҠ” нҷҳкё° кіөлҸҷ лӘЁлҚёмқ„ лҸ„мһ…н•ңлӢӨ. кіөлҸҷмқҳ нҳ•мғҒмқ„ кІ°м •н•ҳкё° мң„н•ҙ Garabedian[7]кіј May[8]мқҳ кіөлҸҷ нҳ•мғҒ мӢқмқ„ мқҙмҡ©н•ҳмҳҖкі мҙҲкё° кіөлҸҷ мҲҳм—җм„ң мӢң뮬л Ҳмқҙм…ҳмқ„ мӢңмһ‘н•ҳм—¬ лӘ©н‘ң кіөлҸҷ мҲҳм—җ мҲҳл ҙлҗҳлҸ„лЎқ нҷҳкё° кіөлҸҷмқҳ к°ҖмҠӨкіөкёүмқҙ мқҙлЈЁм–ҙ진лӢӨкі к°Җм •н•ҳмҳҖлӢӨ. кіөлҸҷмқҳ кёёмқҙмҷҖ мөңлҢҖ л°ҳкІҪмқҖ мӢқ (5)-(6)лҘј нҶөн•ҙ кі„мӮ°лҗҳл©°, мқҙлҘј мқҙмҡ©н•ң мөңмў… кіөлҸҷ н”„лЎңнҢҢмқјмқҖ мӢқ (10)мқ„ нҶөн•ҙ кө¬н• мҲҳ мһҲлӢӨ.
м—¬кё°м—җм„ң RcмқҖ мәҗ비н…Ңмқҙн„° к¶Өм Ғм—җ мҲҳм§Ғмқё л°©н–ҘмңјлЎң нҳ•м„ұлҗң кіөлҸҷмқҳ л°ҳм§ҖлҰ„мқҙлӢӨ.
мәҗ비н…Ңмқҙн„°лҠ” л””мҠӨнҒ¬мқҳ нҳ•нғңлҘј к°Җм§Җл©° н”јм№ҳ 축мңјлЎңл§Ң нҡҢм „н•ҳлҠ” 1мһҗмң лҸ„ мҡҙлҸҷмқ„ н•ңлӢӨ. л¬јкіјмқҳ м ‘мҙүмңјлЎң мқён•ң н•ӯл Ҙ л°Ҹ м–‘л Ҙмқ„ л°ңмғқмӢңнӮӨл©°, мқҙлҘј нҷңмҡ©н•ҙ кіөлҸҷмқ„ нҳ•м„ұн•Ёкіј лҸҷмӢңм—җ мҲҳмӨ‘мҡҙлҸҷмІҙлҘј м ңм–ҙн•ңлӢӨ. ліё м—°кө¬м—җм„ңлҠ” мәҗ비н…Ңмқҙн„°м—җ мқҳн•ң н•ӯл Ҙкі„мҲҳлҠ” Kirschner[9]м—җ мқҳн•ң мӢӨн—ҳк°’ л“ұмқ„ м°ёкі н•ҳл©°, мәҗ비н…Ңмқҙм–ҙм—җ мқҳн•ң м–‘н•ӯл Ҙ мӢқкіј мөңмў… нһҳкіј лӘЁл©ҳнҠёлҠ” Kim & Kim[1вҖ“4]мқ„ м°ёкі н•ҳмҳҖлӢӨ.
Fig. 1кіј к°ҷмқҙ н•ҖмқҖ мҲҳмӨ‘ мҡҙлҸҷмІҙмқҳ нӣ„л©ҙм—җ мң„м№ҳн•ҳл©° 2к°ңмқҳ мҲҳнҸү н•ҖмқҖ м—ҳлҰ¬лІ мқҙн„°, 2к°ңмқҳ мҲҳм§Ғ н•ҖмқҖ лҹ¬лҚ”лқјкі м№ӯн•ңлӢӨ. н•Җм—җ мқҳн•ң нһҳкіј лӘЁл©ҳнҠё мӢқкіј кі„мҲҳлҠ” Kirschner[9]мқҳ мӢӨн—ҳк°’м—җ ліҙк°„лІ•мқ„ мқҙмҡ©н•ҳмҳҖмңјл©°, н•Җм—җ мһ‘мҡ©н•ҳлҠ” нһҳкіј лӘЁл©ҳнҠёлҠ” н•Җмқҳ л°ӣмқҢк°Ғ ОұfмҷҖ м•Ўм№Ё к№Ҡмқҙ dfм—җ л”°лқј кІ°м •лҗңлӢӨ. мһҗм„ён•ң кҙҖл Ё мӢқмқҖ Kim & Kim[1вҖ“4]мқ„ м°ёкі н• мҲҳ мһҲлӢӨ. к°Ғ н•Җм—җм„ң лҸҷмІҙ축мқ„ кё°мӨҖмңјлЎң нҡҢм „ н–үл ¬мқ„ мқҙмҡ©н•ҳл©ҙ н•Җм—җ мқҳн•ң лҸҷмІҙмқҳ л¬ҙкІҢмӨ‘мӢ¬м—җ мһ‘мҡ©н•ҳлҠ” нһҳкіј лӘЁл©ҳнҠёлҘј кө¬н• мҲҳ мһҲлӢӨ. м—¬кё°м„ң, н•Җ мўҢн‘ңкі„мқҳ мӨ‘мӢ¬мқҖ н•Җм—җ мһ‘мҡ©н•ҳлҠ” мң мІҙл Ҙмқҳ м••л Ҙ мӨ‘мӢ¬м—җ мң„м№ҳн•ҳлҜҖлЎң н•Җ мўҢн‘ңкі„мқҳ мӨ‘мӢ¬мқҖ н•Җмқҳ м•Ўм№Ё к№Ҡмқҙм—җ л”°лқј ліҖнҷ”н•ңлӢӨ. мҰү, н•Җмқҳ м•Ўм№ЁмқҖ кіөлҸҷмқҳ мӨ‘мӢ¬кіј л°ҳм§ҖлҰ„ л°Ҹ лҸҷмІҙмқҳ мӨ‘мӢ¬л§Ңмқ„ мқҙмҡ©н•ҳм—¬ мӢӨмӢңк°„мңјлЎң кө¬н•ҙ진лӢӨ.
мҙҲкіөлҸҷ мҲҳмӨ‘мҡҙлҸҷмІҙлҠ” мІңмқҙ мҳҒм—ӯм—җм„ңмқҳ л¶Җ분 кіөлҸҷ н•ҳм—җм„ңлӮҳ кіөлҸҷмқҙ мҷ„м„ұн•ң мқҙнӣ„м—җлҸ„ мң мІҙл Ҙмқҳ мҳҒн–Ҙмқ„ л°ӣлҠ”лҚ° мқҙлҠ” кіөлҸҷмӨ‘мӢ¬м¶• ліҖнҷ”м—җ мқҳн•ҙм„ң мқјл¶Җ лҸҷмІҙмҷҖ н•Җм—җм„ң л¬јкіјмқҳ м ‘мҙүмқҙ мқјм–ҙлӮҳкё° л•Ңл¬ёмқҙлӢӨ. лҸҷмІҙмқҳ м•Ўм№Ё л¶Җмң„м—җ мһ‘мҡ©н•ҳлҠ” мң мІҙл ҘмқҖ л¶Җл Ҙм—җ мқҳн•ң нһҳкіј лӘЁл©ҳнҠё, м••л Ҙм Җн•ӯ л°Ҹ л§Ҳм°°м Җн•ӯ, л¶Җк°Җм§Ҳлҹүм—җ мқҳн•ң мҳҒн–Ҙ л“ұмқҙ мһҲмңјл©°, мқҙм—җ лҢҖн•ң мһҗм„ён•ң мӢқмқҖ Kim & Kim[1вҖ“4]мқ„ м°ёкі н•ҳкё° л°”лһҖлӢӨ.
кіөлҸҷл©ҙмқҙ мғқм„ұлҗң л’Ө мӢңк°„мқҙ м§ҖлӮЁм—җ л”°лқј кіөлҸҷ мӨ‘мӢ¬м¶•мқҖ мЈјліҖ нқҗлҰ„мқҳ көҗлһҖ лҳҗлҠ” мӨ‘л Ҙмқҳ мҳҒн–Ҙм—җ л”°лқј ліҖнҷ”н•ңлӢӨ. ліё л…јл¬ём—җм„ңлҠ” мәҗ비н…Ңмқҙн„° л°ӣмқҢк°Ғкіј мӨ‘л Ҙмқҳ мҳҒн–Ҙмқ„ лӘЁлҚёл§Ғн•ЁмңјлЎңмҚЁ кіөлҸҷ мӨ‘мӢ¬м¶•м—җ мҳҒн–Ҙмқ„ мЈјлҠ” мҡ”мқёмқ„ кі л Өн•ңлӢӨ[1вҖ“4]. Fig. 2мҷҖ к°ҷмқҙ м•Ўм№ЁмқҖ кіөлҸҷ мӨ‘мӢ¬м¶•мқҙ мӨ‘л ҘмқҙлӮҳ мәҗ비н…Ңмқҙн„° л°ӣмқҢк°Ғм—җ мқҳн•ҙ ліҖнҷ”н• кІҪмҡ° YмҷҖ Z축м—җ 비лҢҖм№ӯмқҙ лҗҳкё° л•Ңл¬ём—җ н•Җмқҳ нһҳкіј лӘЁл©ҳнҠё, л¶Җл Ҙ, л§Ҳм°°л Ҙ, Morison нһҳмқ„ кі„мӮ°н•ҳлҠ” лҚ° мҳҒн–Ҙмқ„ лҒјм№ңлӢӨ.
Savchenko[5]мҷҖ Logvinovich[6]лҠ” н•ңм •лҗң кіөлҸҷ мҲҳмҷҖ Froude мҲҳ мЎ°кұҙм—җм„ң мқҙлҘј кІҪн—ҳм ҒмңјлЎң н‘ңнҳ„н•ҳмҳҖмңјл©°, Fig. 3мқҖ кіөлҸҷ мҲҳм—җ л”°лҘё кіөлҸҷмқҳ мӨ‘мӢ¬м¶• ліҖнҷ”лҘј мҶҚлҸ„ 80 m/sм—җм„ң 비көҗн–ҲлӢӨ. ліё л…јл¬ём—җм„ңлҠ” мөңмў…м ҒмңјлЎң Logvinovich[6]мқ„ нҷңмҡ©н–Ҳмңјл©°, кіөлҸҷмҲҳк°Җ 0.1мқ„ мқҙн•ҳлЎң лӮҙл Өк°ҖлҠ” кІҪмҡ° л‘җ лӘЁлҚёмқҳ м°Ёмқҙк°Җ лІҢм–ҙм§ҖлҠ” кІғмқ„ нҷ•мқён–ҲлӢӨ.
н”Ңл ҲмқҙлӢқмқҖ мҲҳмӨ‘мҡҙлҸҷмІҙк°Җ мҙҲкіөлҸҷ мЈјн–ү мӢң лҸҷмІҙмқҳ л’·л¶Җ분мқҙ кіөлҸҷ лІҪм—җ 충лҸҢн• л•Ң л°ңмғқн•ңлӢӨ. Dzielski[10]лҠ” н”Ңл ҲмқҙлӢқ м№ЁмҲҳ к№ҠмқҙмҷҖ мҡҙлҸҷмІҙ нӣ„лҜёмҷҖ кіөлҸҷл©ҙ мӮ¬мқҙмқҳ к°Ғм—җ мқҳн•ҙ н”Ңл ҲмқҙлӢқ нһҳмқ„ м •мқҳн•ң л°” мһҲлӢӨ. ліё л…јл¬ём—җм„ңлҠ” Dzielski[10]мқҳ мҲҳмӢқмқ„ м Ғмҡ©н–Ҳмқ„ л•Ң мҳҲмғҒ мқҙмғҒмңјлЎң нҒ° н”Ңл ҲмқҙлӢқмқҙ мҳҲмёЎлҗҳм–ҙ Yen[11]мқҙ м ңм•Ҳн•ң кІҪн—ҳмӢқмқ„ м Ғмҡ©н–ҲлӢӨ. н”Ңл ҲмқҙлӢқм—җ мқҳн•ң м–‘л Ҙкі„мҲҳлҠ” мӢқ (8)кіј к°ҷмңјл©°, мқҙлҠ” н”Ңл ҲмқҙлӢқ мҳҒм—ӯм—җм„ң нһҳкіј лӘЁл©ҳнҠёлҘј кі„мӮ°н•ҳлҠ”лҚ° мӮ¬мҡ©лҗңлӢӨ.
м—¬кё°м„ң F r = v 2 g R v e h h 0 2 R v e h Оұ
추л ҘмқҖ л¬ҙкІҢмӨ‘мӢ¬м—җм„ң лҸҷмІҙ축 кё°мӨҖ кё°мҲҳ л°©н–ҘмңјлЎңл§Ң мһ‘мҡ©н•ҳкё° л•Ңл¬ём—җ л¬ҙкІҢмӨ‘мӢ¬ мЈјмң„мқҳ лӘЁл©ҳнҠёлҠ” м—Ҷмңјл©°, ліё м—°кө¬м—җм„ңлҠ” мӢқ (9)мҷҖ к°ҷмқҙ мқјм •н•ң нҠёлҰј 추л Ҙмқҙ м Ғмҡ©лҗҳлҠ” кІғмңјлЎң к°Җм •н•ҳмҳҖлӢӨ.
мӨ‘л ҘмқҖ л¬ҙкІҢмӨ‘мӢ¬м—җм„ң мһ‘мҡ©н•ҳм—¬ мӢқ (10)кіј к°ҷмқҙ н”јм№ҳк°Ғ л°Ҹ лЎӨ к°Ғм—җ л”°лқј лҸҷмІҙ축мқ„ кё°мӨҖмңјлЎң ліҖнҷҳн• мҲҳ мһҲмңјл©° мӨ‘л Ҙм—җ мқҳн•ң лӘЁл©ҳнҠё мҳҒн–Ҙ л¬ҙмӢңн•ңлӢӨ.
мЎ°мў…л©ҙмқҳ кө¬лҸҷкё°лҠ” 1м°Ё м „лӢ¬н•ЁмҲҳлЎң м„Өкі„н•ҳмҳҖмңјл©° мӢқ (11)кіј к°ҷкі , лқјн”ҢлқјмҠӨ м—ӯліҖнҷҳмқ„ мҲҳн–үн•ҳл©ҙ мӢқ (12)мҷҖ к°ҷмқҙ м„Өкі„н• мҲҳ мһҲлӢӨ.
м—¬кё°м„ң, П„лҠ” мӢңмғҒмҲҳлҘј мқҳлҜён•ҳл©° xnмқҖ мһ…л Ҙмқҙкі , ynмқҖ кө¬лҸҷкё°лҘј кұ°міҗ лӮҳмҳӨлҠ” м¶ңл ҘмқҙлӢӨ. мӢңмғҒмҲҳлҠ” 0.2лЎң м„Өкі„н•ҳмҳҖлӢӨ.
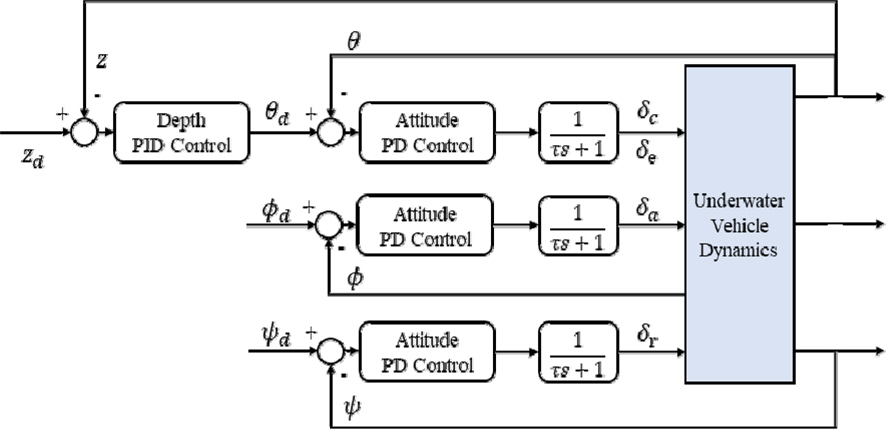
мҲҳмӨ‘мҡҙлҸҷмІҙ мЎ°мў…мқҖ мәҗ비н…Ңмқҙн„°мҷҖ н•Җмқ„ нҶөн•ҙ мҲҳн–үлҗҳл©°, нҠ№нһҲ н•ҖмқҖ м—ҳлҰ¬лІ мқҙн„°мҷҖ лҹ¬лҚ” к°Ғк°Ғ 1мҢҚмңјлЎң кө¬м„ұлҗҳм–ҙ мһҲлӢӨ. мәҗ비н…Ңмқҙн„°лҠ” лҸҷмІҙ м•һм—җм„ң к°ҖмһҘ нҒ° м–‘л Ҙкіј н•ӯл Ҙмқ„ л°ңмғқмӢңнӮӨл©° м§ҲлҹүмӨ‘мӢ¬м—җ лҢҖн•ң лӘЁл©ҳнҠё м•”мқҙ н•ҖліҙлӢӨ мғҒлҢҖм ҒмңјлЎң нҒ¬кё° л•Ңл¬ём—җ мў…л°©н–Ҙ м ңм–ҙм—җ мЈјлҸ„м Ғмқё м—ӯн• мқ„ н•ңлӢӨ. нӣ„л°© м—ҳлҰ¬лІ мқҙн„°лҠ” мәҗ비н…Ңмқҙн„°мҷҖ н•Ёк»ҳ н”јм№ҳк°Ғ м ңм–ҙлҘј мҲҳн–үн• лҝҗл§Ң м•„лӢҲлқј нҡЎл°©н–Ҙ м ңм–ҙлҘј мң„н•ң м°Ёл“ұ мЎ°мў…л©ҙмқҳ м—ӯн• мқ„ мҲҳн–үн•ҳлҠ” кІғмқҙ к°ҖлҠҘн•ҳлӢӨ. лҹ¬лҚ”лҠ” мҡ” л°©н–Ҙ м•Ҳм •нҷ”лҘј мң„н•ҙм„ң мӮ¬мҡ©лҗ мҲҳ мһҲмңјл©° нҠ№нһҲ мҙҲкё° кіөлҸҷмқҙ нҳ•м„ұлҗ л•Ң нҡЁкіјм Ғмқё м•Ҳм •м„ұ мҰқлҢҖ мӢңмҠӨн…ңмңјлЎңмҚЁ мӮ¬мҡ©лҗ мҲҳ мһҲлӢӨ. мӢ¬лҸ„ л°Ҹ мһҗм„ём ңм–ҙмқҳ м „мІҙ лё”лЎқм„ лҸ„лҠ” Fig. 4мҷҖ к°ҷлӢӨ.
мӢ¬лҸ„ м ңм–ҙкё°лҠ” PID м ңм–ҙкё°лЎң кө¬м„ұлҗң мҷёл¶ҖлЈЁн”„мқҙл©° мӢ¬лҸ„лҘј 추종н•ҳлҠ” н”јм№ҳк°Ғ мһҗм„ё лӘ…л №мқ„ мғқм„ұн•ңлӢӨ. мҷёл¶ҖлЈЁн”„лҠ” мӢ¬лҸ„ мҳӨм°Ё z ~
н”јм№ҳк°Ғ м ңм–ҙлҘј мң„н•ҳм—¬ мәҗ비н…Ңмқҙн„° л°Ҹ м—ҳлҰ¬лІ мқҙн„°к°Җ мӮ¬мҡ©лҗҳл©°, мәҗ비н…Ңмқҙн„°лҘј лӢЁлҸ…мңјлЎң мӮ¬мҡ©н• мҲҳлҸ„ мһҲкі м—ҳлҰ¬лІ мқҙн„°мҷҖ лі‘н–үн•ҳм—¬ мӮ¬мҡ©лҗ мҲҳлҸ„ мһҲлӢӨ. н”јм№ҳк°Ғ лӘ… л №мқҖ мӢ¬лҸ„ м ңм–ҙкё°лҘј нҶөн•ҙ мқҙмӨ‘ лЈЁн”„ кө¬мЎ°лЎң м „лӢ¬лҗңлӢӨ. мһҗм„ём ңм–ҙлҠ” н”јм№ҳк°Ғмқ„ м ңм–ҙн•ҳкі PD м ңм–ҙкё°лЎң лҗң лӮҙл¶ҖлЈЁн”„лҘј мқҙмҡ©н•ңлӢӨ. н”јм№ҳк°Ғ мҳӨм°Ё л°Ҹ лӮҙл¶ҖлЈЁн”„мқҳ м ңм–ҙкё° мөңмў… м¶ңл ҘмқҖ мӢқ (15) л°Ҹ (16)кіј к°ҷлӢӨ.
1мҢҚмқҳ лҹ¬лҚ”к°Җ мҡ”к°Ғ м ңм–ҙлҘј мң„н•ҙ мӮ¬мҡ©лҗ мҲҳ мһҲмңјл©°, мҡ”к°Ғ лӘ…л №мқҖ м§Ғ진주н–үмқ„ мң„н•ҳм—¬ 0мңјлЎң м„Өм •лҗңлӢӨ. мһҗм„ём ңм–ҙлҠ” мҡ”к°Ғмқ„ м ңм–ҙн•ҳкі PD м ңм–ҙкё°лЎң мқҙлЈЁм–ҙ진 лӮҙл¶ҖлЈЁн”„лҘј мӮ¬мҡ©н•ңлӢӨ. мҡ”к°Ғ мҳӨм°Ё л°Ҹ лӮҙл¶ҖлЈЁн”„ м ңм–ҙкё° мөңмў…м¶ңл ҘмқҖ мӢқ (17) л°Ҹ (18)кіј к°ҷлӢӨ.
1мҢҚмқҳ м—ҳлҰ¬лІ мқҙн„°лҠ” лЎӨк°Ғ м ңм–ҙлҘј мң„н•ң м°Ёл“ұ мЎ°мў…л©ҙ(differential)мңјлЎңмҚЁ мӮ¬мҡ©лҗ мҲҳ мһҲмңјл©°, м§Ғ진주н–үмқ„ мң„н•ҳм—¬ лЎӨк°Ғ лӘ…л №мқҖ 0мңјлЎң м„Өм •н•ңлӢӨ. мһҗм„ём ңм–ҙм—җм„ңлҠ” лЎӨк°Ғмқ„ м ңм–ҙн•ҳл©°, PD м ңм–ҙкё°лЎң кө¬м„ұлҗң лӮҙл¶ҖлЈЁн”„лҘј мӮ¬мҡ©н•ңлӢӨ. лЎӨк°Ғ мҳӨм°ЁмҷҖ лӮҙл¶ҖлЈЁн”„мқҳ м ңм–ҙкё° мөңмў…м¶ңл ҘмқҖ мӢқ (19) л°Ҹ (20)кіј к°ҷлӢӨ.
мӢ¬лҸ„추종 мң„м№ҳм ңм–ҙкё° л°Ҹ к°Ғ 축мқҳ мһҗм„ём ңм–ҙкё°м—җ мӮ¬мҡ©лҗҳлҠ” м ңм–ҙмқҙл“қмқҖ мӢңн–үм°©мҳӨлҘј нҶөн•ң м„ёл¶ҖмЎ°м •мқ„ кұ°міҗ м„Өкі„ лҗҳм—Ҳмңјл©° мқҙлҘј Table 1м—җ м ңмӢңн•ҳмҳҖлӢӨ.
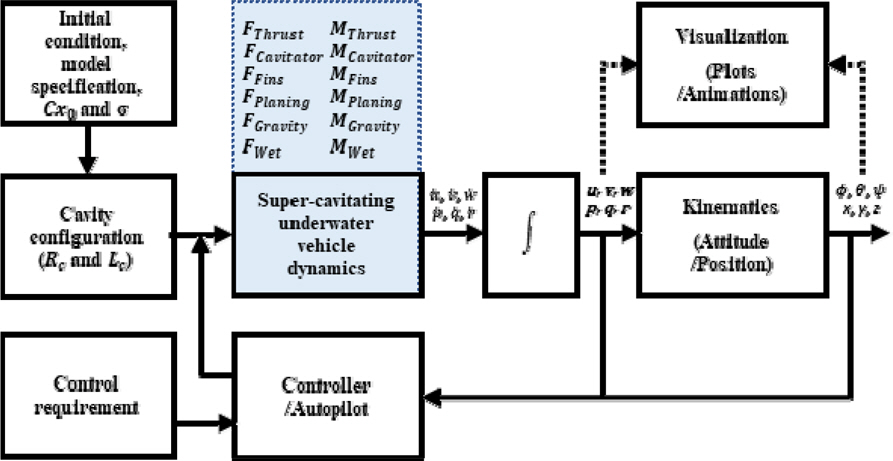
мҙҲкіөлҸҷ мҲҳмӨ‘мҡҙлҸҷмІҙмқҳ мӢң뮬л Ҳмқҙм…ҳ нҷҳкІҪмқҖ Fig. 5мҷҖ к°ҷлӢӨ. кіөлҸҷ мҲҳм—җ л”°лҘё кіөлҸҷмқҳ нҳ•м„ұмқҙ кі„мӮ°лҗҳкі , мқҙлҘј мқҙмҡ©н•ҳм—¬ кіөлҸҷм—җ мқҳн•ң лҸҷмІҙмқҳ м•Ўм№Ёмқҙ кІ°м •лҗңлӢӨ. мқҙлҘј кё°л°ҳмңјлЎң мҷёл¶Җ нһҳкіј лӘЁл©ҳнҠё(추л Ҙ, мӨ‘л Ҙ, мәҗ비н…Ңмқҙн„°, н•Җ, мң мІҙл Ҙ, н”Ңл ҲмқҙлӢқ л“ұ)к°Җ кі„мӮ°лҗҳкі , 6мһҗмң лҸ„ мҡҙлҸҷл°©м •мӢқмқ„ нҶөн•ҙ лҸҷмІҙ축м—җм„ңмқҳ мҶҚлҸ„мҷҖ нҡҢм „к°ҒмҶҚлҸ„к°Җ кІ°м •лҗңлӢӨ. мҡҙлҸҷ м—ӯн•ҷмӢқмқ„ мқҙмҡ©н•ҳм—¬ мҳӨмқјлҹ¬к°ҒмңјлЎң н‘ңнҳ„лҗң 3축мқҳ мһҗм„ёмҷҖ NED мўҢн‘ңкі„м—җм„ңмқҳ мҲҳмӨ‘мҡҙлҸҷмІҙ мң„м№ҳлҘј мөңмў…кІ°м •н•ҳкІҢ лҗңлӢӨ.
мӢңк°„ мҳҒм—ӯм—җм„ңмқҳ м Ғ분мқ„ нҶөн•ҳм—¬ лҸҷмІҙ축 3축 мҶҚлҸ„, 3축 мһҗм„ё к°ҒмҶҚлҸ„, 3축 мҳӨмқјлҹ¬ мһҗм„ёк°Ғ, 3축 мң„м№ҳлЎң кө¬м„ұлҗң 12к°ңмқҳ мғҒнғңліҖмҲҳк°Җ кІ°м •лҗҳкі , мқҙ мӨ‘ мқјл¶ҖлҘј н”јл“ңл°ұ мӢ нҳёлЎң мқҙмҡ©н•ҳм—¬ м ңм–ҙкё°лҘј м„Өкі„н•ҳмҳҖлӢӨ. мӢң뮬л Ҳмқҙм…ҳм—җм„ң мӮ¬мҡ©н•ң мһ…л Ҙк°’кіј мҙҲкё°к°’мқҖ Table 2мҷҖ к°ҷлӢӨ.
Input and initial value
кө¬лҸҷкё°мқҳ мӢңмғҒмҲҳлҠ” 0.2лЎң м„Өм •н•ҳмҳҖмңјл©°, 0.7 мқҙмғҒмқҳ кІҪмҡ° м ңм–ҙм„ұлҠҘмқҙ нҳ„кІ©нһҲ лӮ®м•„м§җмқ„ нҷ•мқён•ҳмҳҖлӢӨ. лҚ”л¶Ҳм–ҙ мәҗ비н…Ңмқҙн„°мқҳ мһ…л Ҙм—җлҠ” Вұ 3В°, лҹ¬лҚ” л°Ҹ м—ҳлҰ¬лІ мқҙн„°м—җлҠ” к°Ғк°Ғ Вұ 10В°мқҳ кө¬лҸҷкё° нҸ¬нҷ”лҘј м„Өм •н•ҳмҳҖлӢӨ.
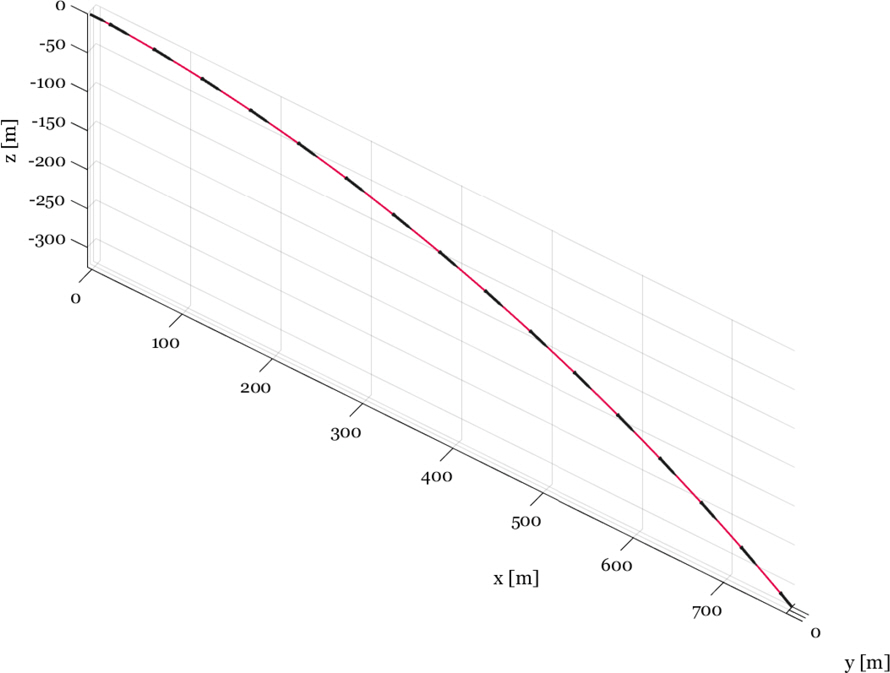
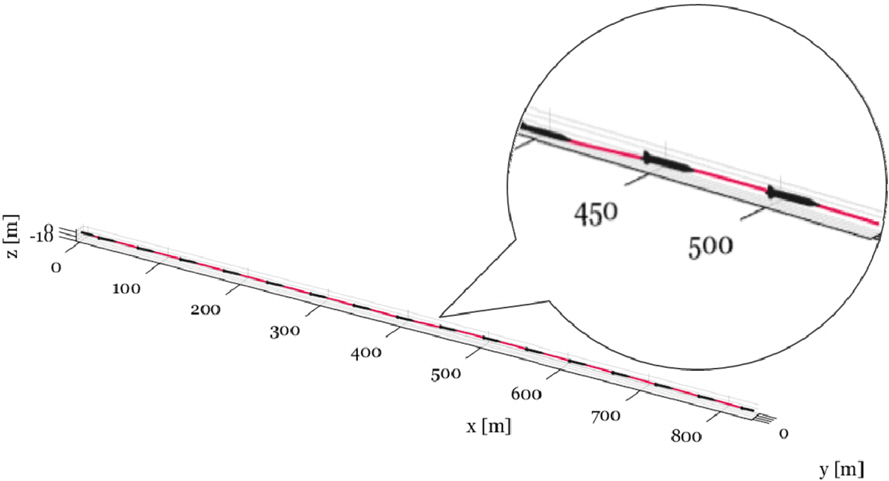
лЁјм Җ м–ҙл– н•ң мЎ°мў…л©ҙлҸ„ мӮ¬мҡ©н•ҳм§Җ м•Ҡкі , мҙҲкё° мЎ°кұҙм—җм„ң 10,000Nмқҳ кі м •лҗң 추л Ҙл§Ңмқ„ к°Җн•ҳм—¬ м§Ғ진м„ұлҠҘмқ„ 분м„қн–ҲлӢӨ. лҸҷмІҙ кёёмқҙлҘј лӘЁл‘җ лҚ®лҠ” кіөлҸҷмқҙ 1мҙҲ мқҙлӮҙм—җ мғқм„ұлҗҳм—Ҳмңјл©° мқҙлЎң мқён•ҙ л¶Җл Ҙкіј мң мІҙл Ҙмқҙ кёүкІ©нһҲ к°җмҶҢн•ҳмҳҖкі , мқҙнӣ„ Fig. 6кіј к°ҷмқҙ мӨ‘л Ҙм—җ мқҳн•ҙ м№Ёк°•н•ҳлҠ” к¶Өм Ғмқҙ нҳ•м„ұлҗҳм—ҲлӢӨ.
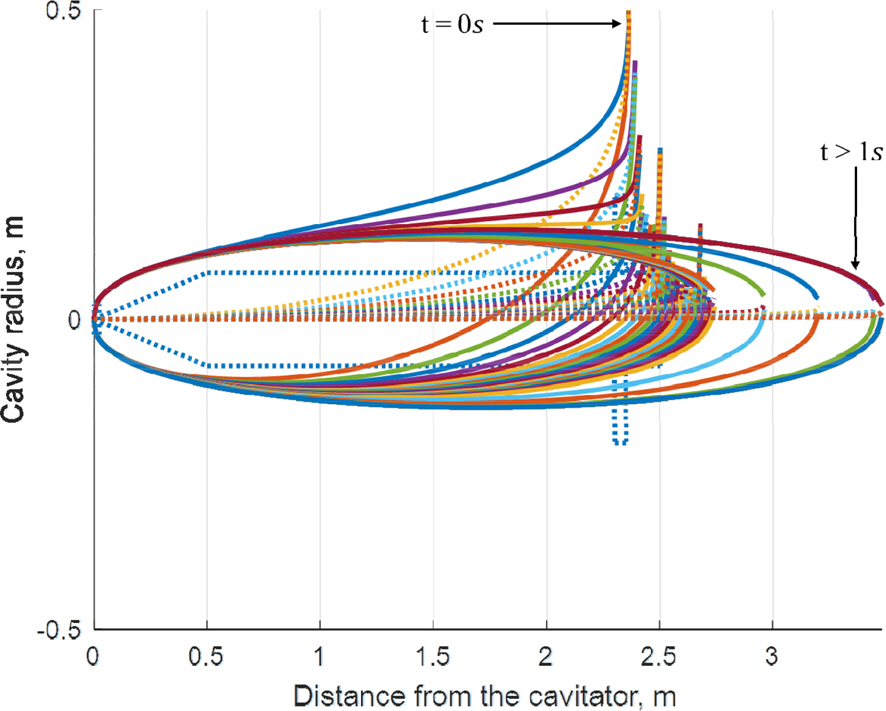
Fig. 7мқҖ мӢңк°„мқҙ м§ҖлӮЁм—җ л”°лҘё кіөлҸҷмқҳ нҳ•мғҒмқ„ лӮҳнғҖлӮёлӢӨ. мҙҲкё°м—җ м ҖмҶҚмқҳ лҶ’мқҖ кіөлҸҷмҲҳм—җм„ңлҠ” л¶Җл Ҙм—җ мқҳн•ң кіөлҸҷ мӨ‘мӢ¬м¶•мқҳ мғҒмҠ№мқҙ нҒ¬кІҢ л°ңмғқн•ҳкІҢ лҗҳкі , мӢңк°„мқҙ м§ҖлӮЁм—җ л”°лқј кі мҶҚм—җм„ңлҠ” м•Ҳм •лҗң кіөлҸҷмқҙ нҳ•м„ұлҗңлӢӨ. мқҙлҹ¬н•ң 비лҢҖм№ӯ кіөлҸҷ нҳ•м„ұмқҖ н•Җкіј н”Ңл ҲмқҙлӢқм—җ мҳҒн–Ҙмқ„ мЈјм–ҙ л¶Ҳм•Ҳм •н•ң нһҳкіј лӘЁл©ҳнҠёлҘј л°ңмғқмӢңнӮЁлӢӨ.
мәҗ비н…Ңмқҙн„°л§Ңмқ„ мқҙмҡ©н•ң кІҪмҡ°лҘј мӢңмһ‘мңјлЎң м—ҳлҰ¬лІ мқҙн„°мҷҖ лҹ¬лҚ”, м°Ёл“ұ мЎ°мў…л©ҙмқ„ 추к°Җ нҷңмҡ©н•ҳм—¬ мҙқ л„Ө к°Җм§Җмқҳ мЎ°мў…л©ҙ мЎ°н•©мқ„ кө¬мғҒн•ҳмҳҖмңјл©° кІ°кіјлҠ” лӢӨмқҢкіј к°ҷлӢӨ.
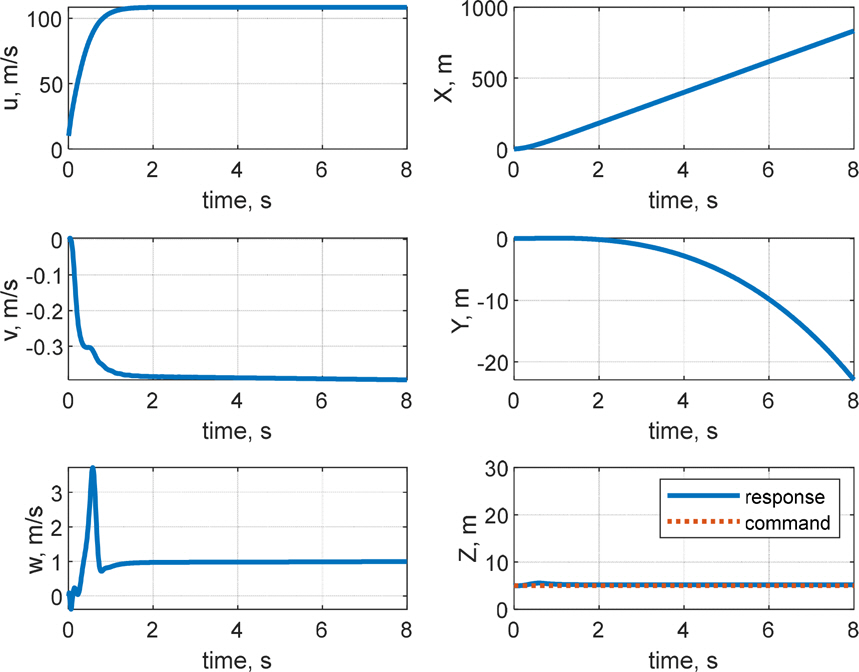
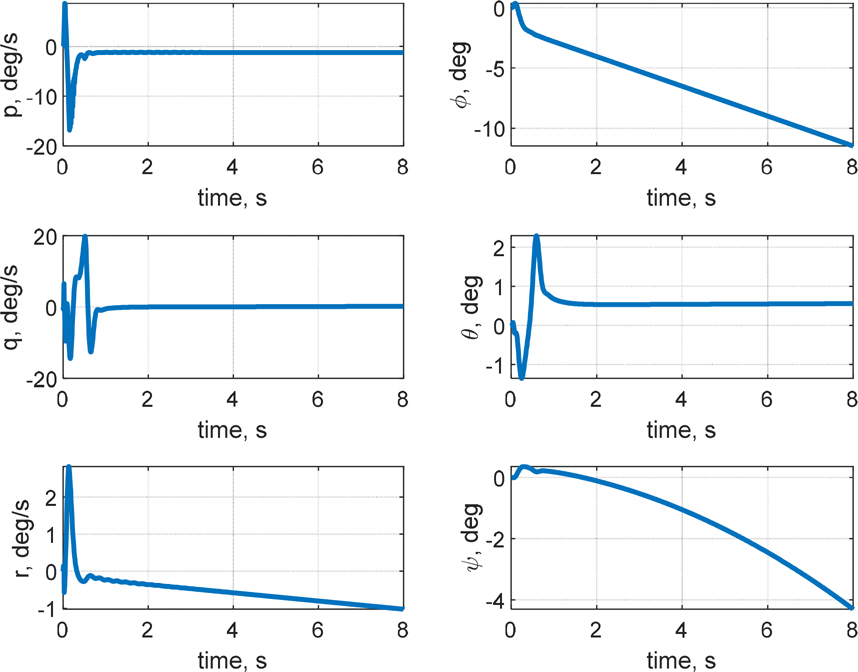
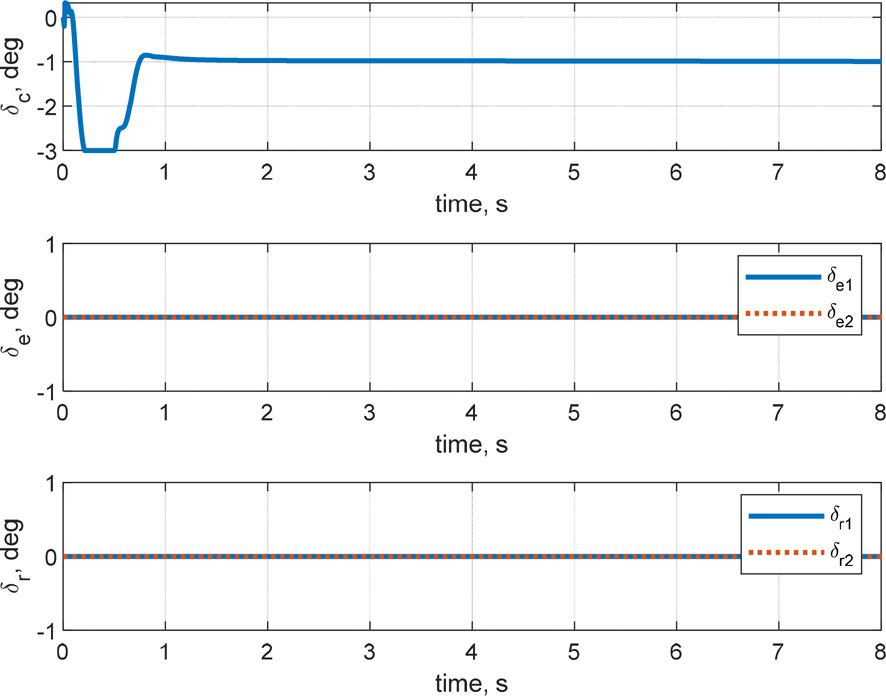
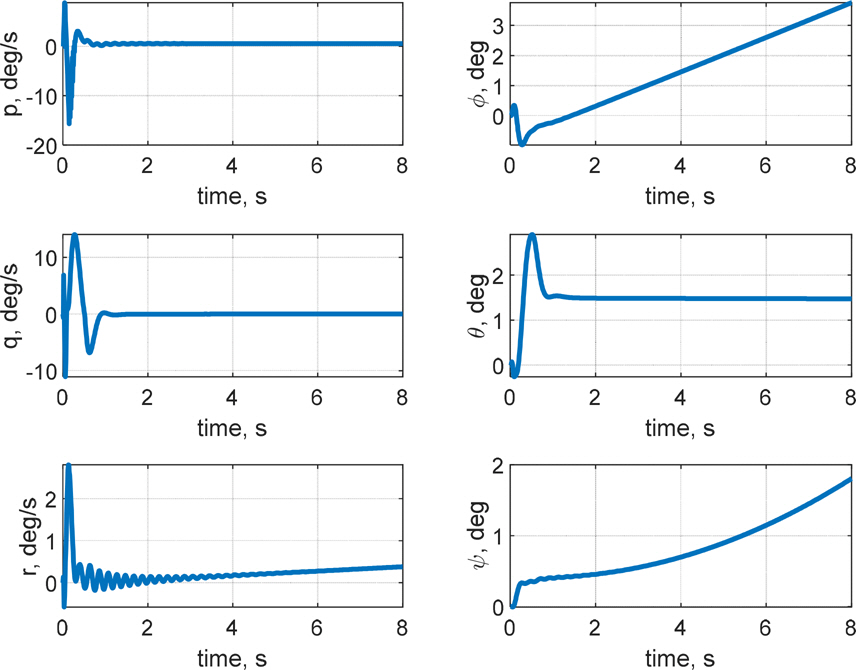
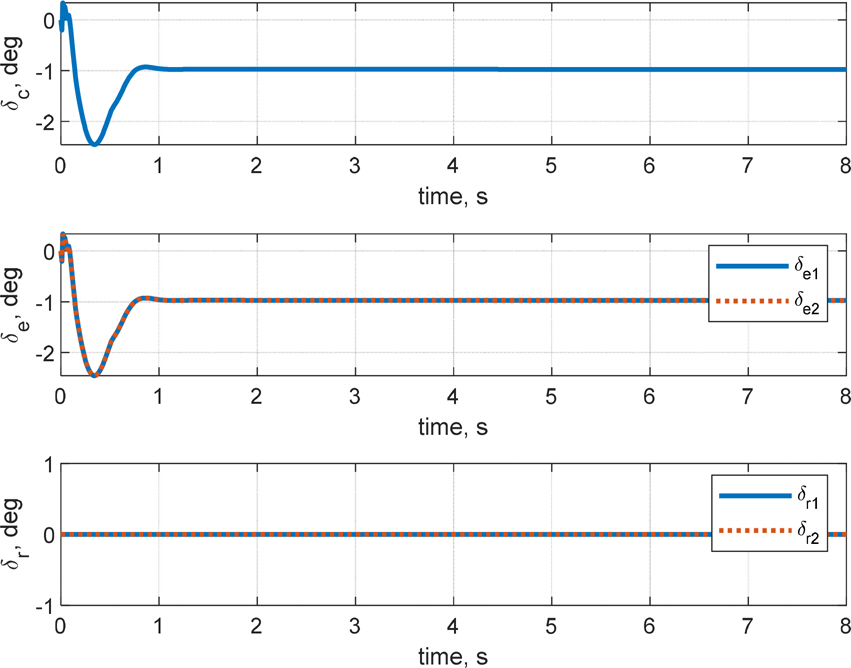
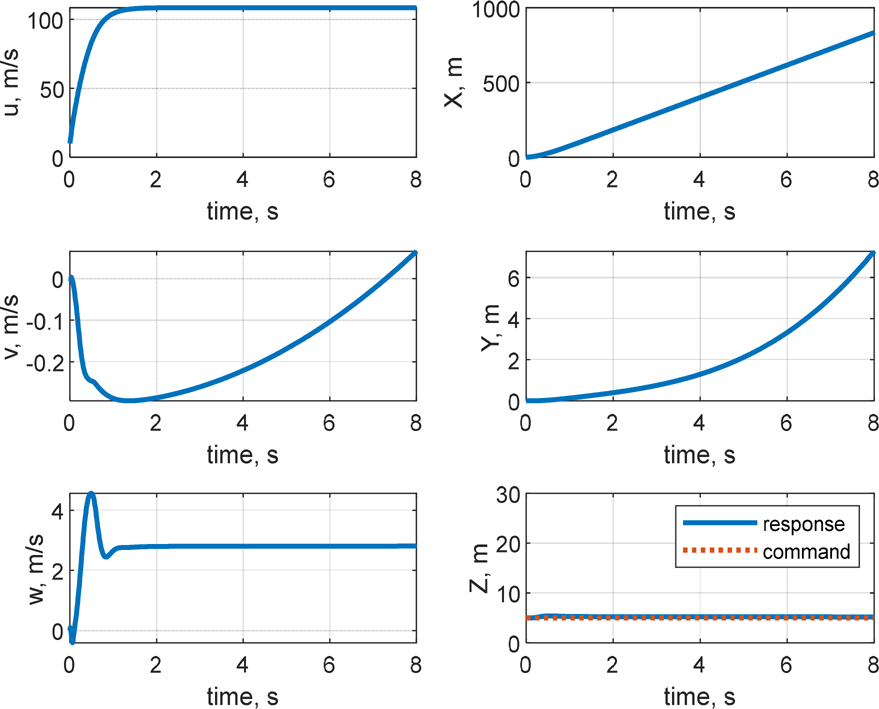
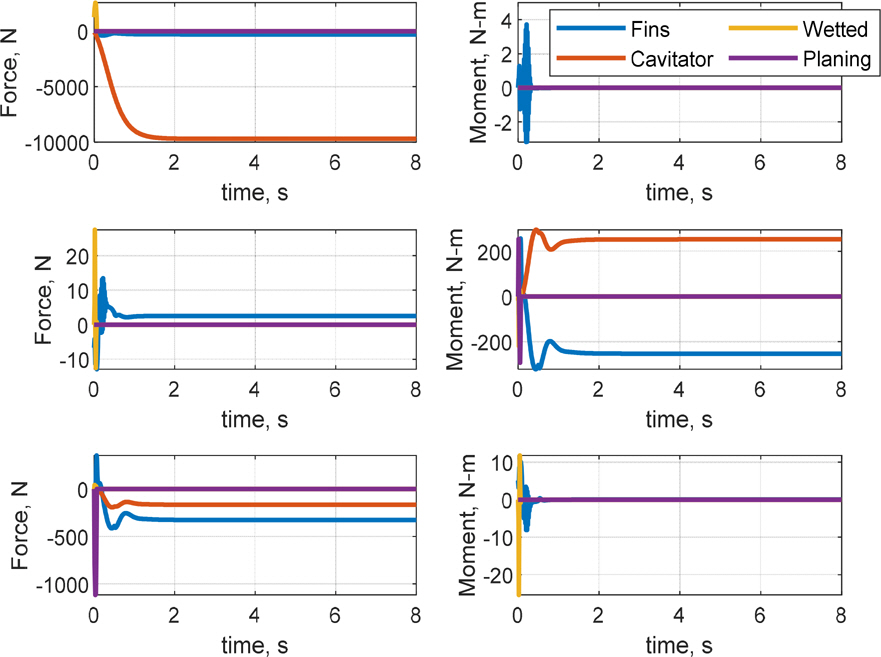
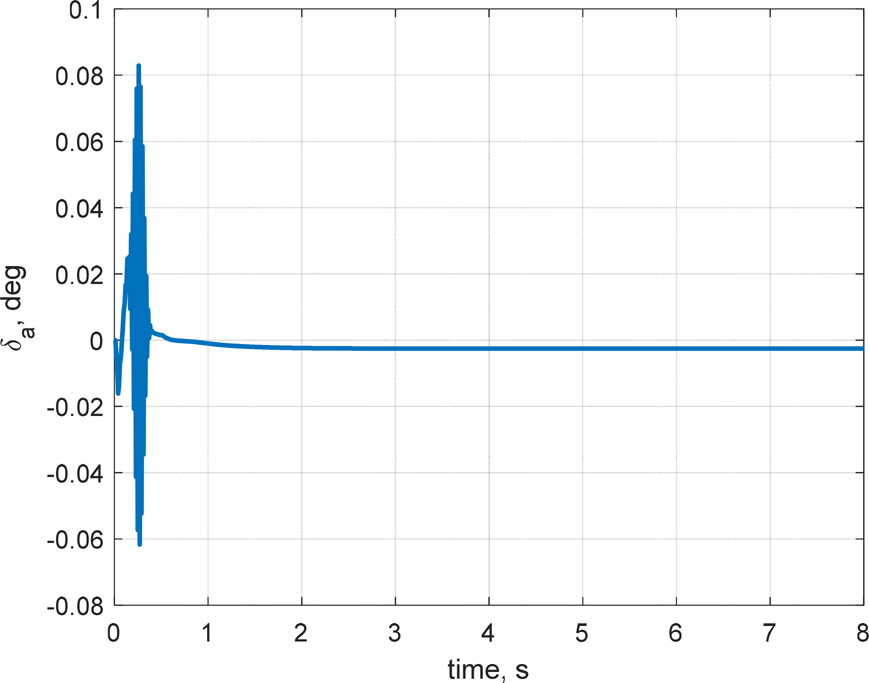
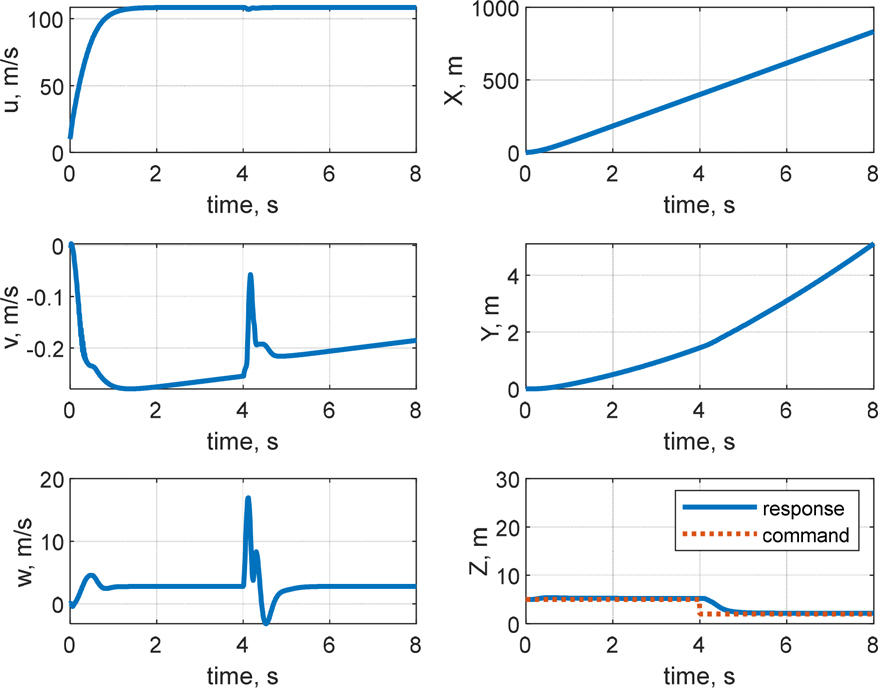
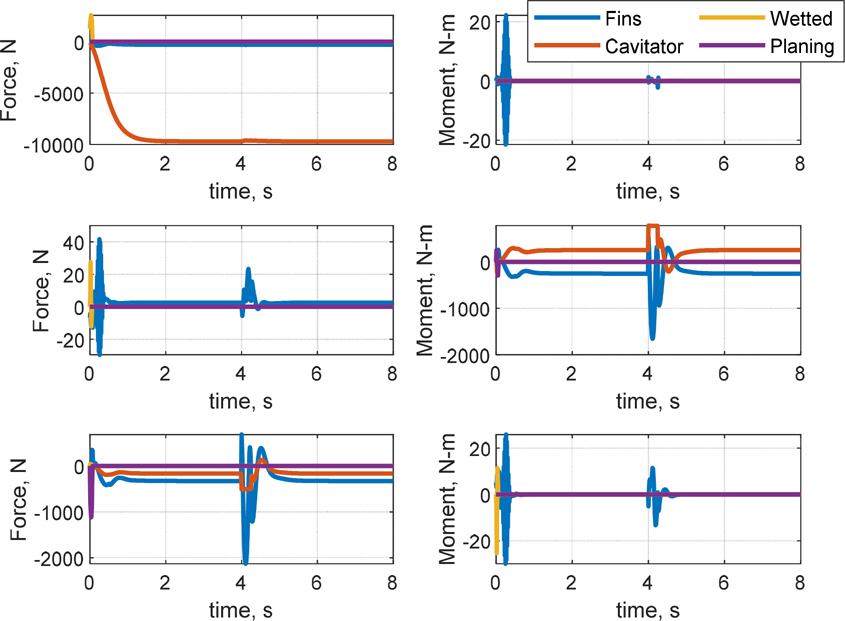
кі м „м ңм–ҙ кё°л°ҳмқҳ мқҙмӨ‘ лЈЁн”„ кө¬мЎ°лҘј м Ғмҡ©н•ҳм—¬ мәҗ비н…Ңмқҙн„°л§Ңмқ„ мқҙмҡ©н•ң мІңмқҙ кө¬к°„ м ңм–ҙ л°Ҹ мӢ¬лҸ„ м ңм–ҙ мҲҳн–үн•ҳмҳҖмңјл©°, мҲҳмӨ‘мҡҙлҸҷмІҙк°Җ мІңмқҙ кө¬к°„ л°Ҹ мҙҲкіөлҸҷ мғҒнғңлҘј м§ҖлӮҳ м •мғҒмғҒнғңм—җ лҸ„лӢ¬н•ң нӣ„ мқјм •н•ң нҠёлҰј к°’мқ„ к°Җм§җмқ„ нҷ•мқён•ҳмҳҖлӢӨ. мӢ¬лҸ„ мҳӨм°Ёк°Җ RMSE кё°мӨҖ м•Ҫ 0.21 m лЎң мӨҖмҲҳн•ң м„ұлҠҘмқ„ ліҙмҳҖмңјлӮҳ мўҢмёЎ лЎӨкіј м„ нҡҢ лӘЁл©ҳнҠёк°Җ л°ңмғқн•ҳмҳҖкі , мўҢмёЎ лЎӨк°Ғкіј н—Өл”©к°Ғ л“ңлҰ¬н”„нҠё(Fig. 10)лЎң мқён•ҙ мөңмў…мңјлЎң Fig. 8кіј Fig. 9м—җм„ң к°ҷмқҙ мўҢмёЎмңјлЎң м•Ҫ 22 m л°Җл ӨлӮ¬лӢӨ. Fig. 11мқ„ ліҙл©ҙ, кіөлҸҷмқҙ нҳ•м„ұлҗҳлҠ” мҙҲкё°м—җ Planingм—җ мқҳн•ң z축 нһҳмқҙ м§Җл°°м ҒмңјлЎң л°ңмғқн•ҳкі , мқҙнӣ„м—җлҠ” м•Ўм№Ёлҗң н•Җмқҳ нһҳкіј лӘЁл©ҳнҠёк°Җ м»Өм§ҖкІҢ лҗңлӢӨ. мҙҲкё°м—җ кіөлҸҷмқҙ нҳ•м„ұлҗҳл©ҙм„ң лҹ¬лҚ”мқҳ мғҒн•ҳ м•Ўм№Ёк№Ҡмқҙк°Җ лӢ¬лқјм§Җл©ҙм„ң мў…л°©н–Ҙ лҝҗ м•„лӢҲлқј нҡЎл°©н–Ҙкіј л°©н–Ҙ축 лӘЁл©ҳнҠёк°Җ нҳ•м„ұлҗҳкі мқҙм—җ л”°лқј мһҗм„ёліҖнҷ”к°Җ мғқкё°л©ҙм„ң мәҗ비н…Ңмқҙн„°лӮҳ н”Ңл ҲмқҙлӢқкіј к°ҷмқҖ лӢӨлҘё мҡ”мқём—җ мқҳн•ң мҷёл Ҙкіј лӘЁл©ҳнҠёк°Җ л°ңмғқн•ҳкІҢ лҗңлӢӨ. Fig. 11м—җм„ң WettedлЎң н‘ңнҳ„лҗң мң мІҙл ҘмқҖ л¶Җл Ҙ, л§Ҳм°°л Ҙ, Morrison нһҳмңјлЎң кө¬м„ұлҗҳлҠ”лҚ°, кіөлҸҷмқҙ нҳ•м„ұлҗЁм—җ л”°лқј л¶Җл ҘмӨ‘мӢ¬мқҙ л’ӨлЎң мқҙлҸҷн•ҳкІҢ лҗҳкі , мҙҲкё°м—җ м–‘мқҳ н”јм№ҳк°Ғмқ„ к°Җм§Ҳ кІҪмҡ° л¶Җл Ҙмқҙ м–‘мқҳ xл°©н–Ҙ нһҳмқ„ к°Җм§ҖкІҢ лҗңлӢӨ. мқҙлҘј м ңм–ҙн•ҳкё° мң„н•ҳм—¬ мҙҲкё° мӢңк°„м—җ мәҗ비н…Ңмқҙн„°к°Җ кө¬лҸҷлҗҳлҠ” кІғмқ„ Fig. 12м—җм„ң нҷ•мқён• мҲҳ мһҲлӢӨ. кІ°кіјм ҒмңјлЎң, л°©н–Ҙ축 л°Ҹ нҡЎм¶•мқ„ м ңм–ҙн•ҳм§Җ м•Ҡмңјл©ҙ м§Ғ진м„ұлҠҘмқҙ мҲҳмӢӯ мҙҲ м•Ҳм—җ мҲҳмӢӯ лҜён„°лҘј л°Җл ӨлӮ м •лҸ„лЎң м Җн•ҳлҗЁмқ„ нҷ•мқён•ҳмҳҖкі , мқҙлҠ” кі§ лҹ¬лҚ”мҷҖ м—ҳлҰ¬лІ мқҙн„°лҘј мқҙмҡ©н•ң л°©н–Ҙ축 л°Ҹ нҡЎм¶• м ңм–ҙмқҳ н•„мҡ”м„ұмқ„ мӢңмӮ¬н•ңлӢӨ.
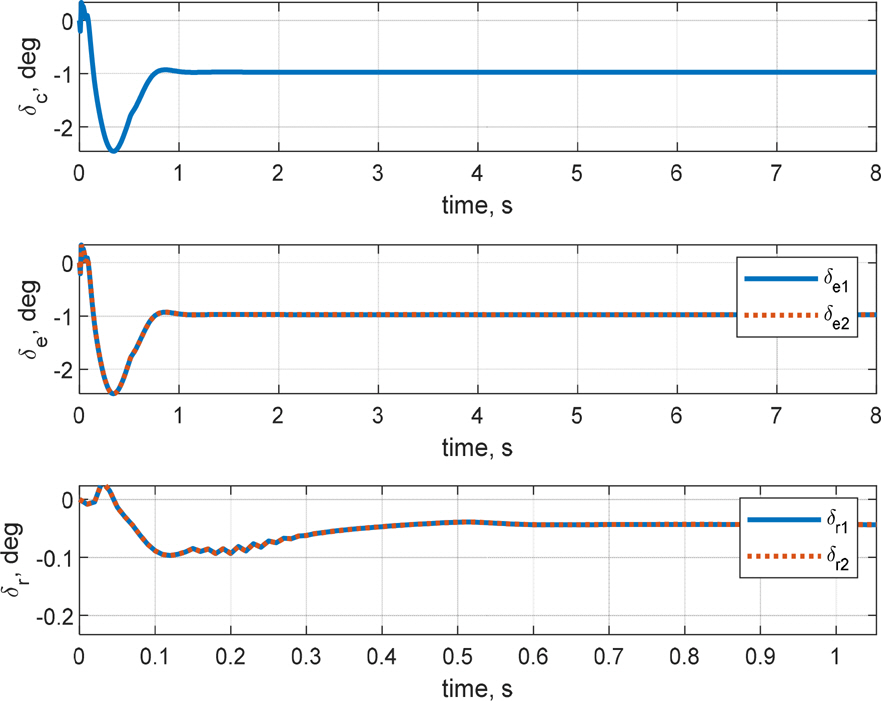
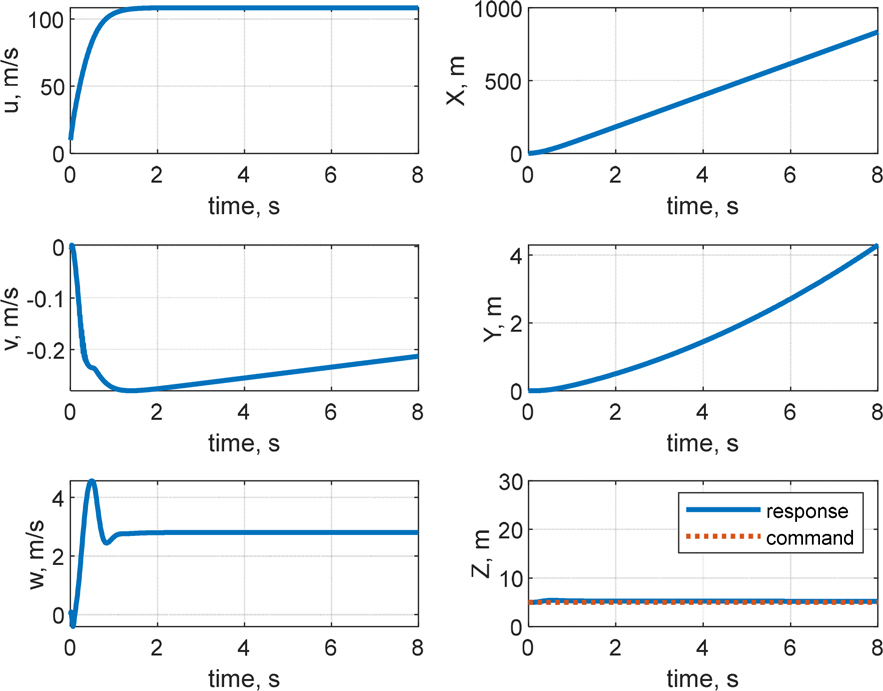
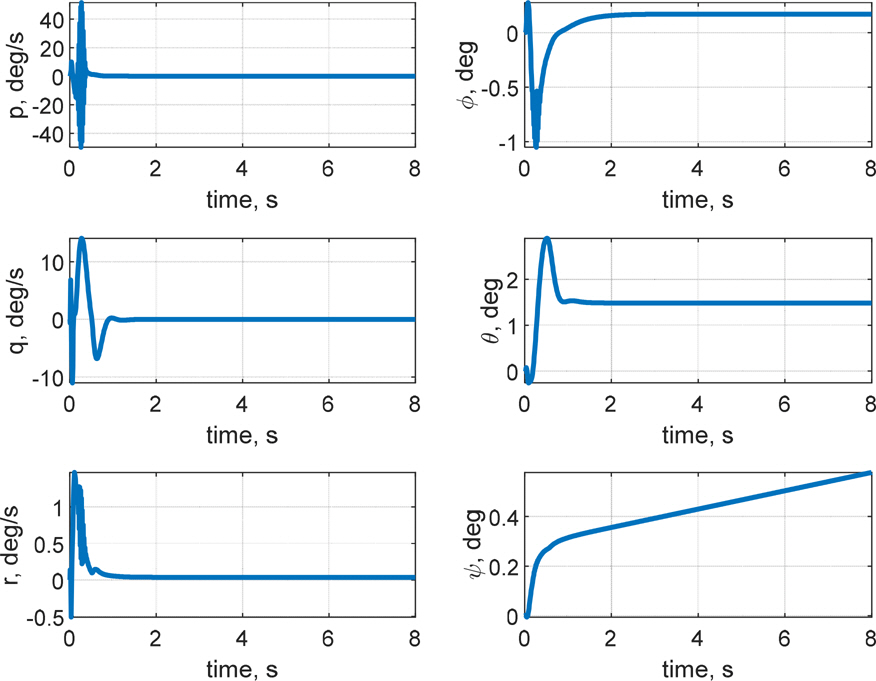
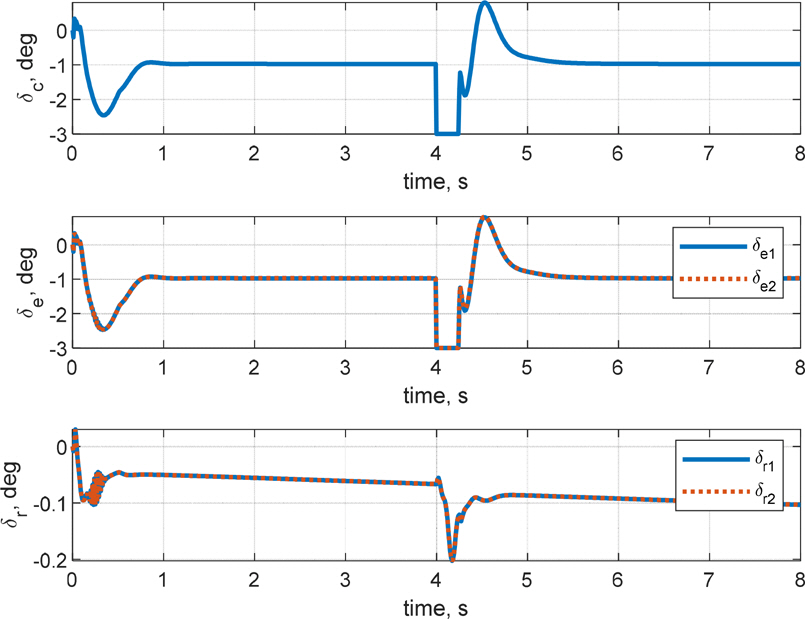
4.1.1 н•ӯмқҳ мәҗ비н…Ңмқҙн„°л§Ңмқ„ мқҙмҡ©н•ң кІҪмҡ°мҷҖ 비көҗн•ҳм—¬ RMSEлЎң ліё мӢ¬лҸ„ м ңм–ҙм„ұлҠҘмқҖ кұ°мқҳ лҸҷмқјн•ң мҲҳмӨҖмқҙл©°, RMSE кё°мӨҖ м§Ғ진м„ұлҠҘмқҖ м•Ҫ 58 % н–ҘмғҒлҗҳм—ҲлӢӨ. Fig. 13мқҳ y축 мң„м№ҳ л°ҳмқ‘мқ„ ліҙл©ҙ 8мҙҲ лҸҷм•Ҳ м•Ҫ 9лҜён„° мўҢмёЎмңјлЎң л°Җл ӨлӮҳлҠ” кІғмқ„ ліј мҲҳ мһҲлӢӨ. Fig. 16кіј к°ҷмқҖ м—ҳлҰ¬лІ мқҙн„°м—җм„ң л°ңмғқн•ҳлҠ” мў…л°©н–Ҙ м ңм–ҙл Ҙмқҙ мҙҲкё° мәҗ비н…Ңмқҙн„°мқҳ ліҖмң„ мҡ”кө¬лҸ„лҘј к°җмҶҢмӢңнӮӨлҠ” нҡЁкіјлҘј л°ңмғқмӢңмј°кі , мқҙлЎң мқён•ҙ кіөлҸҷмқҙ нҳ•м„ұлҗҳлҠ” мҙҲкё°мқҳ м§Ғ진м„ұлҠҘмқҙ н–ҘмғҒлҗҳм—ҲлӢӨ. к·ёлҹ¬лӮҳ Fig. 14вҲј15м—җм„ң ліј мҲҳ мһҲл“Ҝмқҙ м—ҳлҰ¬лІ мқҙн„°мқҳ кІёмҡ©мңјлЎң мқён•ҙ мҙҲкё°м—җ л°©н–Ҙ축 нһҳкіј лӘЁл©ҳнҠём—җ мқҳн•ң 진лҸҷмқҙ л§Һмқҙ л°ңмғқн•ҳкІҢ лҗҳм—Ҳкі , мқҙлЎң мқён•ҙ л°©н–Ҙ축 к°ҒмҶҚлҸ„мҷҖ мёЎл©ҙ мҶҚлҸ„м—җ 진лҸҷмқҙ л°ңмғқн•ҳмҳҖлӢӨ. Fig. 14мқҳ лЎӨк°Ғкіј н—Өл”©к°Ғмқ„ ліҙл©ҙ мӢңк°„м—җ л”°лқј нқҗлҘҙлҠ” кІғмқ„ мӮҙнҺҙліј мҲҳ мһҲлӢӨ.
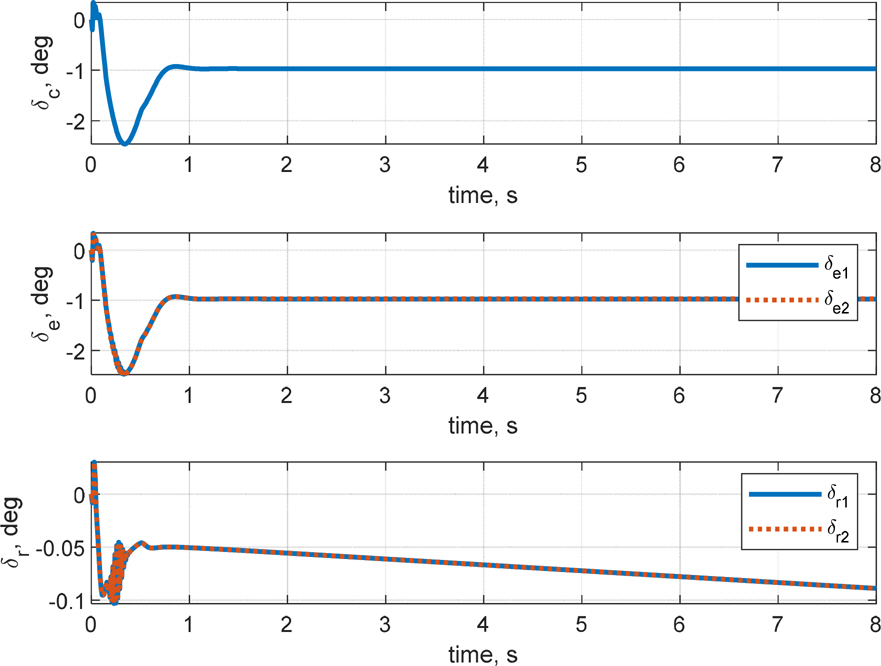
4.1.2 н•ӯм—җм„ң кё°мҲ н•ң л°”мҷҖ к°ҷмқҙ мәҗ비н…Ңмқҙн„°мҷҖ м—ҳлҰ¬лІ мқҙн„°лҘј лҸҷмӢңм—җ мӮ¬мҡ©н•ҳлҠ” кІҪмҡ° л°©н–Ҙ축 진лҸҷ л°ңмғқн•ҳ лҜҖлЎң 진лҸҷ к°җмҶҢлҘј мң„н•ҙ н•ӯкіөкё°м—җ нқ”нһҲ м Ғмҡ©лҗҳлҠ” мҡ”лҢҗнҚј(yaw damper)лҘј мқ‘мҡ©н•ҳм—¬ м„Өкі„н•ҳмҳҖлӢӨ. мқҙлҠ” мҡ”к°Ғмқҳ м•Ҳм •м„ұ мҰқлҢҖлҘј мң„н•ҳм—¬ мҡ”к°ҒмҶҚлҸ„лҘј н”јл“ңл°ұн•ҳлҠ” кІғмқ„ лң»н•ңлӢӨ. к·ё кІ°кіј 4.1.2 н•ӯліҙлӢӨ RMSE м„ұлҠҘмңјлЎң м•Ҫ 22 %мқҳ м§Ғ진м„ұлҠҘмқҙ н–ҘмғҒлҗҳм—Ҳмңјл©°, 4.1.1 н•ӯкіј 비көҗн•ҳл©ҙ м•Ҫ 68 %к°Җ н–ҘмғҒлҗҳм—ҲлӢӨ. Fig. 17мқҳ мӢ¬лҸ„мң м§Җ м„ұлҠҘкіј y축 ліҖмң„ л°ҳмқ‘мқ„ нҶөн•ҙ м§Ғ진м„ұлҠҘ нҷ•мқёмқҙ к°ҖлҠҘн•ҳлӢӨ. нҠ№нһҲ мҡ” лҢҗнҚјмқҳ мӮ¬мҡ©(Fig. 20мқҳ лҹ¬лҚ”ліҖмң„)мңјлЎң мҙҲкё°м—җ л°©н–Ҙ축 нһҳкіј лӘЁл©ҳнҠё(Fig. 19мқҳ z축 л°ҳмқ‘)лЎң мқён•ң н•Җмқҳ 진лҸҷмқҙ к°җмҶҢн•ҳмҳҖкі , мқҙлЎң мқён•ҙ л°©н–Ҙ축 к°ҒмҶҚлҸ„мҷҖ мёЎл©ҙ мҶҚлҸ„м—җ 진лҸҷмқҙ к°җмҶҢн•ҳмҳҖлӢӨлҠ” кІғмқ„ Fig. 18м—җм„ң нҷ•мқён• мҲҳ мһҲлӢӨ. к·ёлҹ¬лӮҳ м—¬м „нһҲ лЎӨ축мқҳ мҙҲкё° 진лҸҷмқҙ лӮЁм•„мһҲкі , лЎӨк°Ғ л°ҳмқ‘мқҙ нқҗлҘҙлҠ” кІғмқ„ ліј мҲҳ мһҲлӢӨ. мқҙлҠ” м—ҳлҰ¬лІ мқҙн„°лҘј м°Ёл“ұ мЎ°мў…л©ҙмңјлЎң мӮ¬мҡ©н• н•„мҡ”м„ұмқ„ мӢңмӮ¬н•ңлӢӨ.
л§Ҳм§Җл§үмңјлЎң лЎӨ 축мқҳ м•Ҳм •м„ұ мҰқлҢҖ л°Ҹ м§Ғ진м„ұлҠҘ н–ҘмғҒмқ„ мң„н•ҳм—¬ м—ҳлҰ¬лІ мқҙн„°лҘј differential мЎ°мў…л©ҙ(мўҢмҡ° м—ҳлҰ¬лІ мқҙн„°лҘј л°ҳлҢҖлЎң мҡҙмҡ©)мңјлЎң нҷңмҡ©н•ҳмҳҖлӢӨ. Fig. 21мқҳ 3м°Ёмӣҗ к¶Өм Ғмқ„ ліҙл©ҙ м§Ғ진м„ұлҠҘмқҙ н–ҘмғҒлҗҳлҠ” кІғмқ„ нҷ•мқён• мҲҳ мһҲмңјл©°, Fig. 22мқҳ y축 мң„м№ҳл°ҳмқ‘мқ„ ліҙл©ҙ 8мҙҲк°„ м•Ҫ 4лҜён„° мҲҳмӨҖм—җм„ң м§Ғ진м„ұлҠҘмқ„ мң м§Җн•ҳкі мһҲлӢӨ. Fig. 23мқҳ мһҗм„ёк°ҒмҶҚлҸ„мҷҖ мһҗм„ёк°Ғ л°ҳмқ‘м—җм„ңлҸ„ мқҙм „ кІҪмҡ°ліҙлӢӨ м•Ҳм •нҷ”лҗҳм—Ҳмңјл©°, лЎӨк°Ғкіј н—Өл”©к°ҒмқҖ 1лҸ„ м •лҸ„мқҳ мҲҳмӨҖм—җм„ң м ңм–ҙлҗҳкі мһҲлӢӨ. Fig. 25мқҳ мЎ°мў…л©ҙ ліҖмң„лҘј ліҙл©ҙ м°Ёл“ұмЎ°мў…л©ҙмқҳ к°’мқҖ лӢӨлҘё мЎ°мў…л©ҙмқҳ ліҖмң„ліҙлӢӨ мғҒлҢҖм ҒмңјлЎң мһ‘м§Җл§Ң мҙҲкё° мӢңк°„м—җм„ңмқҳ лЎӨк°Ғ нқҗлҰ„мқ„ нҶөм ңн•ҳл©ҙм„ң м „мІҙм Ғмқё м§Ғ진м„ұлҠҘм—җ кё°м—¬н•ҳмҳҖлӢӨ. Fig. 24лҠ” н•ҙлӢ№мӢңк°„ лҸҷм•Ҳ м°Ё л“ұмЎ°мў…л©ҙ лҸҷмһ‘мңјлЎң мқён•ҙ Finм—җ мқҳн•ң лӘЁл©ҳнҠёк°Җ лӢӨлҘё caseл“ӨліҙлӢӨ мҰқк°Җн•ҳмҳҖмқҢмқ„ м•Ң мҲҳ мһҲлӢӨ. Fig. 26мқҖ м—ҳлҰ¬лІ мқҙн„°м—җ лҢҖн•ң м°Ёл“ұмЎ°мў…л©ҙ к°’мқ„ лі„лҸ„лЎң ліҙм—¬мЈјкі мһҲмңјл©°, мҙҲкё° мӢңк°„м—җ кё°лҜјн•ҳкІҢ лҸҷмһ‘н•ҳм—¬ лЎӨк°Ғмқ„ м ңм–ҙн•ҳкі , мҙҲкё° мӢңк°„ мқҙнӣ„м—җлҸ„ мқјм •н•ң нҠёлҰјк°’мңјлЎң мҲҳл ҙн•ҳм—¬ лЎӨк°Ғмқҙ нқҗлҘҙлҠ” нҳ„мғҒмқ„ нҡЁкіјм ҒмңјлЎң нҶөм ңн•ҳкі мһҲлӢӨ.
мӢ¬лҸ„ л°Ҹ м§Ғ진м„ұлҠҘмқ„ 분м„қн•ҳкё° мң„н•ҙ 4к°Җм§Җ мЎ°н•©м—җ лҢҖн•ң мӢ¬лҸ„추종 мҳӨм°ЁмҷҖ м§Ғ진м„ұлҠҘ мҳӨм°ЁлҘј Table 3м—җ мҡ”м•Ҫн–ҲлӢӨ. мӢ¬лҸ„추종мқҳ кІҪмҡ° л„Ө кІҪмҡ°к°Җ нҒ° м°Ёмқҙк°Җ м—ҶмңјлӮҳ, м§Ғ진м„ұлҠҘмқҳ кІҪмҡ° мәҗ비н…Ңмқҙн„°л§Ңмқ„ мӮ¬мҡ©н•ҳлҠ” кІҪмҡ°ліҙлӢӨ лҹ¬лҚ”мҷҖ м°Ёл“ұ мЎ°мў…л©ҙмқ„ нҳјмҡ©н•ң кІҪмҡ°к°Җ мҡ°мҲҳн•Ёмқ„ нҷ•мқён–ҲлӢӨ. нҠ№нһҲ м°Ёл“ұмЎ°мў… к°ңл…җмқ„ м—ҳлҰ¬лІ мқҙн„°м—җ м Ғмҡ©н• кІҪмҡ° лҹ¬лҚ”лҘј лҸ„мһ…н•ң кІҪмҡ°ліҙлӢӨ лҚ” нҒ° к°ңм„ нҡЁкіјлҘј м–»мқ„ мҲҳ мһҲлҠ” кІғмқ„ мәҗ비н…Ңмқҙн„°л§Ңмқ„ мӮ¬мҡ©н•ң кІҪмҡ° лҢҖ비 к°ңм„ мңЁ(%)лҘј мҰқк°ҖмңЁмқ„ ліҙл©ҙ м•Ң мҲҳ мһҲлӢӨ.
Control performance analysis
Fig. 12лҘј ліҙл©ҙ мәҗ비н…Ңмқҙн„°л§Ңмқ„ мӮ¬мҡ©н• кІҪмҡ° мҙҲл°ҳл¶Җ 0.3мҙҲ м •лҸ„мқҳ мӢңк°„лҸҷм•Ҳ нҸ¬нҷ”лҗҳл©°, мқҙнӣ„ лӢӨлҘё мЎ°мў…л©ҙмқ„ мЎ°н•©н• кІҪмҡ°м—җлҠ” нҸ¬нҷ”лҗҳм§Җ м•ҠлҠ” кІғмқ„ нҷ•мқён• мҲҳ мһҲлӢӨ.мәҗ비н…Ңмқҙн„°лҠ” мҙҲкё° кіөлҸҷмғқм„ұм—җлҸ„ мӨ‘мҡ”н•ҳкІҢ кҙҖм—¬н•ҳкі мһҲкё° л•Ңл¬ём—җ мЎ°мў…л Ҙмқ„ мӢ¬н•ҳкІҢ мӮ¬мҡ©н• кІҪмҡ° мӢңмҠӨн…ңмқҳ 진лҸҷнҠ№м„ұмқҙ м•Ҳ мўӢм•„м§Җкі л§Өмҡ° л№ лҘё мӢңк°„м—җ л¶Ҳм•Ҳм •н•ҳкІҢ л§Ңл“ңлҠ” нҠ№м„ұмқ„ к°Җм§Җкі мһҲлӢӨ. мӢӨм ң мҡҙмҡ© мӢңм—җлҠ” мҙҲкіөлҸҷ мҲҳмӨ‘мҡҙлҸҷмІҙмқҳ мҶҚлҸ„ нҠ№м„ұм—җ л”°лқј нҸ¬нҷ” м •лҸ„лҘј мЎ°м Ҳн•ҙм•ј н• н•„мҡ”м„ұмқҙ мһҲлӢӨ.
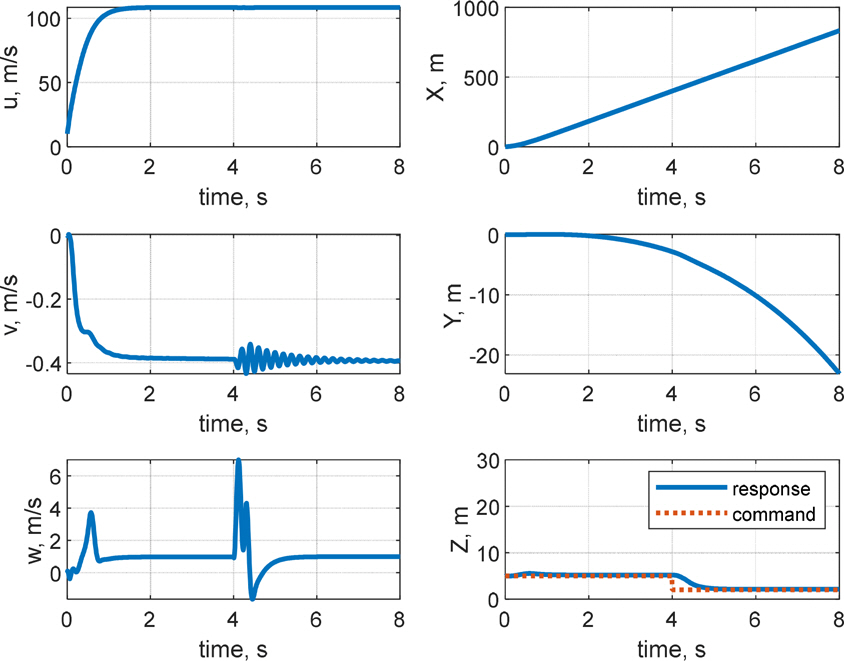
ліё м—°кө¬м—җм„ң м ңм•Ҳлҗң мЎ°мў…л©ҙ мЎ°н•©мқҳ к°ҖліҖ мӢ¬лҸ„ лӘ…л №мқҳ 추종 м„ұлҠҘмқ„ нҢҢм•…н•ҳкё° мң„н•ҳм—¬ 4мҙҲ м „м—җлҠ” 5 mмқҳ лӘ…л №, мқҙнӣ„м—җлҠ” 2 mмқҳ лӘ…л №мқ„ мқёк°Җн•ҳмҳҖмңјл©°, мЎ°мў…л©ҙмқ„ лӘЁл‘җ нҳјмҡ©н•ҳм—¬ м Ғмҡ©н• кІҪмҡ° 4мҙҲм—җ к°ҖліҖкі лҸ„ лӘ…л №мқҙ мқёк°Җлҗҳкі , м•Ҳм •м ҒмңјлЎң мӢ¬лҸ„ 2 mм—җ мҲҳл ҙн•ҳлҠ” кІғмқ„ Fig. 27кіј Fig. 28м—җм„ң нҷ•мқён• мҲҳ мһҲлӢӨ. Fig. 29лҠ” мһҗм„ёк°ҒмҶҚлҸ„мҷҖ мһҗм„ёк°Ғмқ„ ліҙм—¬мЈјл©°, к°ҖліҖ кі лҸ„лҘј 추종н•ҳкё° мң„н•ҳм—¬ 4мҙҲм—җ н”јм№ҳк°Ғ ліҖнҷ”к°Җ л°ңмғқлҗҳкі м»Өн”Ңл§ҒмңјлЎң мқён•ң лӢӨлҘё 축м—җм„ңмқҳ мҡҙлҸҷлҸ„ кҙҖм°°лҗңлӢӨ. лЎӨмқҖ м°Ёл“ұмЎ°мў…л©ҙмңјлЎң мқён•ҙ 0лҸ„ к·јмІҳм—җм„ң мң м§Җлҗҳкі мһҲмңјл©°, н—Өл”©к°Ғ лҳҗн•ң лҹ¬лҚ”м—җ мқҳн•ҙ 1лҸ„ мқҙлӮҙм—җм„ң м ңм–ҙлҗҳкі мһҲлӢӨ. Fig. 30мқҖ 4мҙҲмқҳ к°ҖліҖкі лҸ„ 추종мқ„ мң„н•ң мҷёл Ҙкіј мҷёл¶ҖлӘЁл©ҳнҠёмқҳ кёүкІ©н•ң ліҖнҷ”лҘј ліҙм—¬мЈјкі мһҲмңјл©°, Fig. 31вҖ“32лҠ” кіөлҸҷнҳ•м„ұ мҙҲкё°мҷҖ к°ҖліҖкі лҸ„ 추종 мӢңмқҳ м°Ёл“ұмЎ°мў…л©ҙмқҳ кё°лҜјн•ң лӘ…л №мқ„ ліҙм—¬мӨҖлӢӨ.
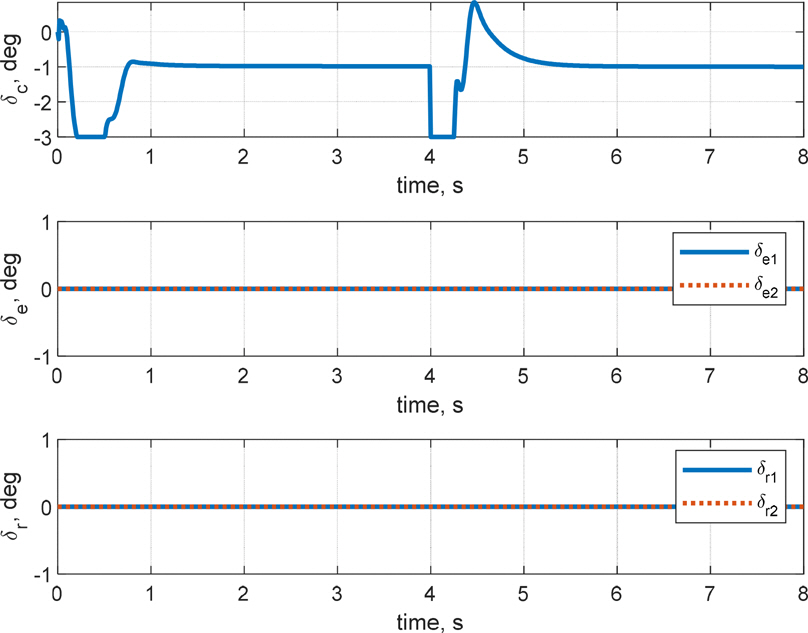
Fig. 33вҲј36мқҖ мәҗ비н…Ңмқҙн„°л§Ңмқ„ м Ғмҡ©н•ң к°ҖліҖ кі лҸ„추종 кІ°кіјлҘј ліҙм—¬мЈјкі мһҲлӢӨ. Fig. 33мқҳ кҙҖм„ұмўҢн‘ңкі„ мң„м№ҳ л°Ҹ лҸҷмІҙ축 мҶҚлҸ„мҷҖ Fig, 34мқҳ мһҗм„ёл°ҳмқ‘кіј Fig. 35мқҳ мҷёл Ҙкіј лӘЁл©ҳнҠёлҘј ліҙл©ҙ, мәҗ비н…Ңмқҙн„°л§Ң мӮ¬мҡ©н•ң кІҪмҡ° к°ҖліҖкі лҸ„к°Җ мқёк°Җлҗң нӣ„мқҳ л°ҳмқ‘мқҙ мғҒлӢ№нһҲ л¶Ҳм•Ҳм •н•ҳкі м§„лҸҷмқҙ л§ҺмқҖ кІғмқ„ ліј мҲҳ мһҲлӢӨ. нҠ№нһҲ Y축 мң„м№ҳ к·ёлһҳн”„лҘј ліҙл©ҙ, 4.3м Ҳм—җм„ң л…јмқҳн•ң л°”мҷҖ к°ҷмқҙ л°©н–Ҙ축 л°Ҹ нҡЎм¶•мқ„ м ңм–ҙн•ҳм§Җ м•Ҡмңјл©ҙ м§Ғ진м„ұлҠҘмқҙ м•Ҫ 20 m мқҙмғҒ л°Җл ӨлӮ м •лҸ„лЎң м Җн•ҳлҗЁмқ„ нҷ•мқён• мҲҳ мһҲлӢӨ.
кІ°кіјм ҒмңјлЎң ліё м—°кө¬лҘј нҶөн•ҙм„ң м„Өкі„лҗң лӢӨмӨ‘ мЎ°мў…л©ҙ мЎ°н•©мқ„ нҶөн•ң PID лӢӨмӨ‘лЈЁн”„ м ңм–ҙкө¬мЎ°к°Җ к°ҖліҖ мӢ¬лҸ„ лӘ…л №мқ„ 추종н•ҳлҠ” лҚ°лҸ„ нҡЁкіјм ҒмңјлЎң м Ғмҡ©лҗ мҲҳ мһҲмқҢмқ„ нҷ•мқён•ҳмҳҖлӢӨ.
ліё м—°кө¬м—җм„ңлҠ” мҙҲкіөлҸҷ мҲҳмӨ‘мҡҙлҸҷмІҙмқҳ 6мһҗмң лҸ„ лӘЁлҚёл§Ғкіј мһҗм„ё л°Ҹ мӢ¬лҸ„ м ңм–ҙлҘј мң„н•ң м ңм–ҙкё°лҘј м„Өкі„н•ҳмҳҖлӢӨ. лҳҗн•ң, мқҙлҘј мқҙмҡ©н•ҳм—¬ мӢң뮬л Ҳмқҙм…ҳ нҷҳкІҪмқ„ кө¬м¶•н•ҳмҳҖмңјл©° мҙҲкіөлҸҷ мҲҳмӨ‘мҡҙлҸҷмІҙмқҳ мЎ°мў…л©ҙ мЎ°н•©м—җ лҢҖн•ң м•Ҳм •м„ұ н•ҙм„қ л°Ҹ мЈјн–үм„ұлҠҘмқ„ 분м„қн•ҳмҳҖлӢӨ. мәҗ비н…Ңмқҙн„°лҝҗл§Ң м•„лӢҲлқј м—ҳлҰ¬лІ мқҙн„°, лҹ¬лҚ” л°Ҹ м°Ёл“ұ мЎ°мў…л©ҙмқ„ лҸҷмӢңм—җ м Ғмҡ©н•ң кІҪмҡ° л°©н–Ҙ축 л°Ҹ нҡЎм¶•мқҳ м•Ҳм •нҷ”лЎң мқён•ҙ мӢ¬лҸ„ м ңм–ҙм„ұлҠҘмқҙ м„ұкіөм ҒмңјлЎң н–ҘмғҒлҗЁмқ„ нҷ•мқён•ҳмҳҖлӢӨ. лӢӨл§Ң, н•Җмқҳ мң мІҙкі„мҲҳлӮҳ н”Ңл ҲмқҙлӢқ нһҳм—җ лҢҖн•ҳм—¬ л¬ён—ҢлҚ°мқҙн„°к°Җ нҷңмҡ©лҗң л¶Җ분м—җ мһҲм–ҙм„ңлҠ” лӘЁлҚёл§Ғ л¶Ҳнҷ•мӢӨм„ұмқҙ м–ҙлҠҗ м •лҸ„ лҗҳлҠ”м§Җ к°ҖлҠ н•ҳкё°к°Җ нҳ„мһ¬лЎңм„ңлҠ” м–ҙл өлӢӨлҠ” м җмқ„ кі л Өн•ҙм•ј н•ңлӢӨ. ліё м—°кө¬мқҳ кІ°кіјлҠ” н–Ҙнӣ„ мҙҲкіөлҸҷ мҲҳмӨ‘мҡҙлҸҷмІҙмқҳ м ңм–ҙкё°лІ• к°ңл°ң мӢңм—җ мЎ°мў…л©ҙкіј мЎ°мў…л Ҙ 분배 л“ұ м ңм–ҙкё° м„Өкі„ л°Ҹ кІҖмҰқмқ„ мң„н•ң 분м„қ лҸ„кө¬лЎңмҚЁ нҷңмҡ©лҗ мҲҳ мһҲмңјл©° к°ңл…җ м„Өкі„ мӢңмқҳ м„Өкі„ кІҖнҶ мһҗлЈҢлЎңмҚЁлҸ„ м°ёкі лҗ мҲҳ мһҲмқ„ кІғмңјлЎң кё°лҢҖлҗңлӢӨ.
References
[1] S. H. Kim and N. Kim, "Study on Dynamics Modeling and Depth Control for a Supercavitating Underwater Vehicle in Transition Phase," Journal of the Society of Naval Architects of Korea, Vol. 51, No. 1, pp. 88вҖ“98, 2014.

[2] S. H. Kim and N. Kim, "Hydrodynamics and Modeling of a Ventilated Supercavitating Body in Transition Phase," Journal of Hydrodynamics, Vol. 27, No. 5, pp. 763вҖ“772, 2015.

[3] N. Kim, A Study on L1 Adaptive Control based Operation Envelope Protection for a Supercavitating Underwater Vehicle, Ph.D. Dissertation, Seoul National University. 2018.
[4] S. Kim and N. Kim, "Integrated Dynamics Modeling for Supercavitating Vehicle Systems," International Journal of Naval Architecture and Ocean Engineering, Vol. 7, No. 2, pp. 346вҖ“363, 2015.

[5] Y. N. Savchenko, Expermental Investigation of Supercavitating Motion of Bodies, UKRAINIAN ACADEMY OF SCIENCES KIEV INST OF HYDROMECHANICS. 2001.
[6] G. V. Logvinovich and V. V. Serebryakov, On Methods of Calculating form of Slender Axisymmetric Cavities, J. Hydromech 32. pp. 47вҖ“54, 1975.
[7] P. R. Garabedian, "Calculation of Axially Symmetric Cavities and Jets," Pacific Journal of Mathematics, Vol. 6, No. 4, pp. 611вҖ“684, 1956.

[8] A. May, Water Entry and the Cavity-Running Behavior of Missiles(No. SEAHAC/TR-75-2), Navsea Hydroballistics Advisory Committee Silver Spring Md. 1975.
[9] I. N. Kirschner, D. C. Kring, A. W. Stokes, N. E. Fine and J. S. Uhlman Jr, "Control Strategies for Supercavitating Vehicles," Journal of Vibration and Control, Vol. 8, No. 2, pp. 219вҖ“242, 2002.

[10] J. E. Dzielski, "Longitudinal Stability of a Supercavitating Vehicle," IEEE Journal of Oceanic Engineering, Vol. 36, No. 4, pp. 562вҖ“570, 2011.

[11] Timothy Yen et al, "Investigation of Cylinder Planing on a Flat Free Surface," 11th International Conference on Fast Sea Transportation FAST, Vol. 2011, 2011.