|
 |
- Search
| J. KIMS Technol > Volume 24(4); 2021 > Article |
|
Abstracts
Raman spectrometers are studied and developed for the military purposes because of their nondestructive inspection capability to capture unique spectral features induced by molecular structures of colorless and odorless chemical warfare agents(CWAs) in any phase. Raman spectrometers often suffer from random noise caused by their detector inherent noise, background signal, etc. Thus, reducing the random noise in a measured Raman spectrum can help detection algorithms to find spectral features of CWAs and effectively detect them. In this paper, we propose a denoising autoencoder for Raman spectra with a loss function for sample efficient learning using noisy dataset. We conduct experiments to compare its effect on the measured spectra and detection performance with several existing noise reduction algorithms. The experimental results show that the denoising autoencoder is the most effective noise reduction algorithm among existing noise reduction algorithms for Raman spectrum based standoff detection of CWAs.
ĒÖöņāØļ░® ņāüĒÖ® ļ░£ņāØ ņŗ£ ĒÖöĒĢÖņĀü ņ£äĒśæņ£╝ļĪ£ ņØĖĒĢ£ Ēö╝ĒĢ┤ļź╝ ņĄ£ņåīĒÖöĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ĒÖöĒĢÖļ¼╝ņ¦łņØś ņŗĀņåŹĒĢ£ ĒāÉņ¦Ć ļ░Å ļīĆņ▓śĻ░Ć ĒĢäņÜöĒĢśļŗż. ĒĢśņ¦Ćļ¦ī ņ£ĀļÅģņä▒ ĒÖöĒĢÖņ×æņÜ®ņĀ£ ņżæņŚÉļŖö ļ¼┤ņāē, ļ¼┤ņĘ©ņØś ĒŖ╣ņä▒ņØä Ļ░Ćņ¦ä ļ¼╝ņ¦łņØ┤ ļ¦ÄĻĖ░ ļĢīļ¼ĖņŚÉ Ļ░Ćņŗ£Ļ┤æņäĀ ņØ┤ņÖĖņØś Ēīīņן ļīĆņŚŁņŚÉņä£ ĒÖöĒĢÖņ×æņÜ®ņĀ£ļź╝ ņ░ŠļŖö ļ╣äņĀæņ┤ēņŗØ ĒāÉņ¦ĆĻĖ░ņłĀņØś ĒĢäņÜöņä▒ņØ┤ ņĀÉņĀÉ ļīĆļæÉļÉśĻ│Ā ņ׳ļŗż[1].
ĻĘĖļ¤¼ĒĢ£ ĒāÉņ¦ĆĻĖ░ņłĀ ņżæ ĒĢśļéśļĪ£ņŹ©, ļ¬©ļōĀ ņāüĒā£ņØś ļ¼╝ņ¦łņØä ļ╣äĒīīĻ┤┤ņĀüņ£╝ļĪ£ ļČäņäØĒĢĀ ņłś ņ׳ļŖö ļ╣äņĀæņ┤ēņŗØ ļØ╝ļ¦ī ļČäĻ┤æĻ│ä(Raman Spectrometer)Ļ░Ć ņŚ░ĻĄ¼ļÉśĻ│Ā ņ׳ļŗż[2]. ļØ╝ļ¦ī ļČäĻ┤æĻ│äļŖö ļĀłņØ┤ņĀĆļź╝ ļ¼╝ņ¦łņŚÉ ņĪ░ņé¼ĒĢĀ ļĢī ļ░£ņāØĒĢśļŖö ļ¼╝ņ¦łņØś ļØ╝ļ¦ī ņé░ļ×ĆĻ┤æņØä ņĖĪņĀĢĒĢśļŖö ņןļ╣äņØ┤ļŗż. ļØ╝ļ¦ī ņé░ļ×ĆĻ┤æņØś ņŖżĒÄÖĒŖĖļ¤╝ņØ┤ ļ¼╝ņ¦łņØś ļČäņ×ÉĻĄ¼ņĪ░ ļ░Å ĒŖ╣ņä▒ņŚÉ ļö░ļØ╝ Ļ│Āņ£ĀĒĢ£ ĒśĢĒā£ļź╝ ļØĀĻĖ░ ļĢīļ¼ĖņŚÉ ļØ╝ļ¦ī ļČäĻ┤æĻ│äļŖö ĒÖöĒĢÖņ×æņÜ®ņĀ£ ĒāÉņ¦ĆņŚÉ ņ£ĀņÜ®ĒĢśĻ▓ī ņé¼ņÜ®ļÉĀ ņłś ņ׳ļŗż[3]. ĻĄ¼ņ▓┤ņĀüņ£╝ļĪ£, ņ£ĀļÅģņä▒ ĒÖöĒĢÖņ×æņÜ®ņĀ£Ļ░Ć ņ¦ĆĒæ£ļ®┤ņŚÉ ņé┤ĒżļÉ£ ņāüĒÖ®ņŚÉņä£ ņØ┤ļź╝ ņŗĀņåŹĒ׳ ĒāÉņ¦ĆĒĢśĻĖ░ ņ£äĒĢ┤ ņ░©ļ¤ēņŚÉ ļØ╝ļ¦ī ļČäĻ┤æĻ│äļź╝ Ēāæņ×¼ĒĢśņŚ¼ ņ░©ļ¤ē ņØ┤ļÅÖ ņżæņŚÉ ņ¦ĆĒæ£ļ®┤ņØś ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØä ņĖĪņĀĢĒĢśĻ│Ā ĒÖöĒĢÖņ×æņÜ®ņĀ£ņŚÉ ņśżņŚ╝ļÉ£ ņśüņŚŁņØä ĒīÉļŗ©ĒĢśļŖö ņŗ£ņŖżĒģ£[4]ņØ┤ ĻĄ░ņé¼ņĀüņ£╝ļĪ£ ņŚ░ĻĄ¼ļÉśĻ│Ā ņ׳ļŗż.
ļØ╝ļ¦ī ļČäĻ┤æĻ│äļĪ£ ĒÜŹļōØĒĢ£ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØĆ ļ░░Ļ▓Į ņŗĀĒśĖ, Ļ▓ĆņČ£ĻĖ░ņØś ļé┤ņ×¼ņĀüņØĖ ļ¼ĖņĀ£ ļō▒ ņŚ¼ļ¤¼ ņØ┤ņ£ĀļĪ£ ņØĖĒĢ┤ ņ×ĪņØī ņä▒ļČäņØä ĒżĒĢ©ĒĢśĻ│Ā ņ׳ļŗż[5]. ņØ┤ļ¤¼ĒĢ£ ņ×ĪņØī ņä▒ļČä ļĢīļ¼ĖņŚÉ ļØ╝ļ¦ī ļČäĻ┤æĻ│äļŖö ĒÖöĒĢÖņ×æņÜ®ņĀ£ņØś ļ¬ģĒÖĢĒĢ£ ĒŖ╣ņ¦Ģ ĒīīĒśĢņØä ĒÖĢļ│┤ĒĢśĻĖ░ ņ¢┤ļĀĄļŗż[6]. ļö░ļØ╝ņä£ ļ╣äņĀæņ┤ēņŗØ ļØ╝ļ¦ī ļČäĻ┤æĻ│ä ĻĖ░ļ░ś ņ£ĀļÅģņä▒ ĒÖöĒĢÖņ×æņÜ®ņĀ£ ĒāÉņ¦Ć ņŗ£ņŖżĒģ£ņŚÉņä£ ņŗżņÜ®ņĀüņØĖ ĒāÉņ¦Ćņä▒ļŖźņØä ĒÖĢļ│┤ĒĢśĻĖ░ ņ£äĒĢ┤ņä£ļŖö ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņŚÉņä£ ļ×£ļŹż ņ×ĪņØīņØä ņĀ£Ļ▒░ĒĢśļŖö Ļ│╝ņĀĢņØ┤ ĒĢäņÜöĒĢśļŗż.
ļØ╝ļ¦ī ļČäĻ┤æĻ│äļĪ£ ņĖĪņĀĢĒĢ£ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØś ņ×ĪņØīņØä ņĀ£Ļ▒░ĒĢśļŖö ļ░®ļ▓Ģņ£╝ļĪ£ļŖö ĻĖ░ņĪ┤ ņ┤łļČäĻ┤æ ņŖżĒÄÖĒŖĖļ¤╝ ņŚ░ĻĄ¼ņØś ņ×ĪņØīņĀ£Ļ▒░ ĻĖ░ļ▓ĢņØä ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ņØæņÜ®ĒĢśļŖö ņŚ░ĻĄ¼[5,7ŌĆō9]ļź╝ ņŻ╝ļĪ£ ņ░ŠņĢäļ│╝ ņłś ņ׳ļŗż. ĒĢśņ¦Ćļ¦ī ņØ╝ļČĆ ļØ╝ļ¦ī ļČäĻ┤æĻ│ä ņĀüņÜ® ļČäņĢ╝ņŚÉņä£ļŖö ĻĖ░ņĪ┤ ņ┤łļČäĻ┤æ ņŖżĒÄÖĒŖĖļ¤╝ņØś ņ×ĪņØīņĀ£Ļ▒░ ņŚ░ĻĄ¼ņÖĆ ņ░©ņØ┤ļź╝ ļ│┤ņØ┤ļŖö ļČĆļČäņØ┤ ņ׳ļŗż. ņØ╝ļ░śņĀüņ£╝ļĪ£ ņ┤łļČäĻ┤æ ņŖżĒÄÖĒŖĖļ¤╝ņØś ņ×ĪņØīņĀ£Ļ▒░ļŖö ļ│ĄņłśņØś ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│ĖņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņ×ĪņØīņØä ņĀ£Ļ▒░ĒĢśļŖö ļ░®ļ▓ĢņØ┤ ņŻ╝ļź╝ ņØ┤ļŻ¼ļŗż[10]. ļ░śļ®┤ņŚÉ ņ░©ļ¤ē ņØ┤ļÅÖ ņżæņŚÉ ņ¦ĆĒæ£ļ®┤ņŚÉ ņé┤ĒżļÉ£ ĒÖöĒĢÖņ×æņÜ®ņĀ£ņØś ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØä ņĖĪņĀĢĒĢśļŖö ĒāÉņ¦Ć ņŗ£ņŖżĒģ£ņØś ņŚ░ĻĄ¼ņŚÉņä£ļŖö ņŗżņĀüņÜ® ņāüĒÖ®ņØä Ļ░ĆņĀĢĒĢĀ ļĢī ļÅÖņØ╝ ļīĆņāüņŚÉ ļīĆĒĢ┤ ļ│ĄņłśņØś ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│ĖņØä ĒÜŹļōØĒĢśĻĖ░ ņ¢┤ļĀżņÜ░ļ»ĆļĪ£ ļŗ©ņØ╝ ņŖżĒÄÖĒŖĖļ¤╝ļ¦īņØä ņØ┤ņÜ®ĒĢ£ ņ×ĪņØīņĀ£Ļ▒░ ĻĖ░ļ▓ĢņØä ņĀüņÜ®ĒĢśļŖö ņŚ░ĻĄ¼[11]Ļ░Ć ņØ┤ļŻ©ņ¢┤ņ¦äļŗż. ļö░ļØ╝ņä£ ĻĖ░ņĪ┤ ņ┤łļČäĻ┤æ ņŖżĒÄÖĒŖĖļ¤╝ ņŚ░ĻĄ¼ņŚÉņä£ ļŗ©ņØ╝ ņŖżĒÄÖĒŖĖļ¤╝ļ¦īņ£╝ļĪ£ ņ×ĪņØīņØä ņĀ£Ļ▒░ĒĢśĻĖ░ ņ£äĒĢ£ ņ×ĪņØīņĀ£Ļ▒░ ĻĖ░ļ▓ĢņØĖ Savitzky-Golay ĒĢäĒä░(S-G filter), ĒæĖļ”¼ņŚÉ ļ│ĆĒÖś, ņØ┤ļÅÖ ĒÅēĻĘĀ, ņżæĻ░äĻ░Æ ĒĢäĒä░ ļō▒ņØä ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ņØæņÜ®ĒĢśļŖö ņŚ░ĻĄ¼[5,7ŌĆō9]Ļ░Ć ņłśĒ¢ēļÉśņŚłļŗż.
ņŗ¼ņĖĄ ĒĢÖņŖĄņØś ļ░£ņĀäĻ│╝ ĒĢ©Ļ╗ś ņØĖĻ│Ą ņŗĀĻ▓Įļ¦Ø ĻĖ░ļ░ś ņ×ĪņØīņĀ£Ļ▒░ ĻĖ░ļ▓ĢņØĖ denoising autoencoder(DAE)ļź╝ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØś ņ×ĪņØīņĀ£Ļ▒░ņŚÉ ņĀüņÜ®ĒĢśļŖö ņŚ░ĻĄ¼[12]ļÅä ņłśĒ¢ēļÉśņŚłļŗż. DAE ņØś ĒĢÖņŖĄņØä ņ£äĒĢ┤ņä£ļŖö ņ×ĪņØīņØ┤ ņŚåļŖö Ēæ£ļ│ĖĻ│╝ ņ×ĪņØīņØ┤ ņ׳ļŖö Ēæ£ļ│ĖņØä ļ¬©ļæÉ ļ│┤ņ£ĀĒĢ£ ļŹ░ņØ┤Ēä░ņģŗņØä ĒÖĢļ│┤ĒĢ┤ņĢ╝ ĒĢ£ļŗż[13]. ĒĢ┤ļŗ╣ ņŚ░ĻĄ¼ņŚÉņä£ļŖö ļåÆņØĆ ņČ£ļĀźņØś ļĀłņØ┤ņĀĆļĪ£ ņĖĪņĀĢĒĢ£ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØä ņ×ĪņØīņØ┤ ņŚåļŖö Ēæ£ļ│Ėņ£╝ļĪ£ Ļ░ĆņĀĢĒĢśĻ│Ā, ļé«ņØĆ ņČ£ļĀźņØś ļĀłņØ┤ņĀĆļĪ£ ņĖĪņĀĢĒĢ£ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØä ņ×ĪņØīņØ┤ ņ׳ļŖö Ēæ£ļ│Ėņ£╝ļĪ£ Ļ░ĆņĀĢĒĢśņŚ¼ DAEļź╝ ĒĢÖņŖĄĒĢ£ļŗż[12]. ĒĢśņ¦Ćļ¦ī ņāüĻĖ░ ņĀæĻĘ╝ļ▓ĢņØĆ ņä£ļĪ£ ļŗżļźĖ ņČ£ļĀźņØä Ļ░Ćņ¦ä ļæÉ Ļ░£ ņØ┤ņāüņØś ļĀłņØ┤ņĀĆļź╝ ļ│┤ņ£ĀĒĢ£ ņāüĒÖ®ņŚÉņä£ļ¦ī ņ£ĀĒÜ©ĒĢśļ®░, ļŗ©ņØ╝ ņČ£ļĀź ļĀłņØ┤ņĀĆļ¦ī ļ│┤ņ£ĀĒĢ£ Ļ▓ĮņÜ░ ņāüĻĖ░ ņĀæĻĘ╝ļ▓ĢņØä ņĀüņÜ®ĒĢĀ ņłś ņŚåļŗżļŖö ĒĢ£Ļ│äņĀÉņØä Ļ░Ćņ¦ĆĻ│Ā ņ׳ļŗż.
ļ│Ė ļģ╝ļ¼ĖņØĆ ļŗ©ņØ╝ ņČ£ļĀź ļĀłņØ┤ņĀĆļ¦ī ļ│┤ņ£ĀĒĢ£ ņāüĒÖ®ņŚÉņä£ ĒÖĢļ│┤ĒĢĀ ņłś ņ׳ļŖö ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ļŹ░ņØ┤Ēä░ņģŗņ£╝ļĪ£ DAEļź╝ ĒÜ©ņ£©ņĀüņ£╝ļĪ£ ĒĢÖņŖĄĒĢśĻĖ░ ņ£äĒĢ£ ļ░®ļ▓ĢņØä ņĀ£ņĢłĒĢ£ļŗż. ļŗ©ņØ╝ ņČ£ļĀź ļĀłņØ┤ņĀĆļĪ£ ņĖĪņĀĢĒĢ£ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│ĖņŚÉļŖö ņ×ĪņØīņØ┤ ņĪ┤ņ×¼ĒĢśļ®░, ņ×ĪņØīņØ┤ ņ׳ļŖö ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│Ėļ¦īņ£╝ļĪ£ ņ×ĪņØīņĀ£Ļ▒░ ĻĖ░ļŖźņØä ĒĢÖņŖĄĒĢśĻĖ░ ņ£äĒĢ£ ļ░®ļ▓Ģņ£╝ļĪ£ņŹ© ļŹ░ņØ┤Ēä░ņģŗ ļé┤ ņØĖĻĘ╝ Ēæ£ļ│ĖņØś ņĀĢļ│┤ļź╝ Ēæ£ļ│Ė ĒÜ©ņ£©ņĀüņ£╝ļĪ£ ĒÖ£ņÜ®ĒĢśļŖö ņåÉņŗż ĒĢ©ņłśļź╝ ņĀ£ņĢłĒĢ£ļŗż. ņØ┤ļź╝ ĒåĄĒĢ┤ ņØ┤ļÅÖ ņżæņØĖ ņ░©ļ¤ēņŚÉņä£ ļØ╝ļ¦ī ļČäĻ┤æĻ│äļĪ£ ņ¦ĆĒæ£ļ®┤ņŚÉ ņé┤ĒżļÉ£ ĒÖöĒĢÖņ×æņÜ®ņĀ£ņØś ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØä ņĖĪņĀĢĒĢśļŖö ĒāÉņ¦Ć ņŗ£ņŖżĒģ£ņØä ņ£äĒĢ£ DAE ĻĖ░ļ░ś ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØä ĻĄ¼ĒśäĒĢ£ļŗż. ņŗżĒŚśņØä ĒåĄĒĢ┤ ĻĖ░ņĪ┤ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śĻ│╝ ļ╣äĻĄÉĒĢśņŚ¼ ņ×ĪņØīņĀ£Ļ▒░ ņĀä/Ēøä ļØ╝ļ¦ī ņŗĀĒśĖņØś ņä▒ņ¦ł ļ│ĆĒÖöļź╝ ļČäņäØĒĢ£ļŗż. ļéśņĢäĻ░Ć Ļ░ü ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śļ¦łļŗż ĒāÉņ¦Ć ņĢīĻ│Āļ”¼ņ”śņØä ņĀüņÜ®ĒĢśņŚ¼ ņ×ĪņØīņĀ£Ļ▒░ ņĀä/Ēøä ĒāÉņ¦Ćņä▒ļŖź ļ│ĆĒÖöļź╝ ļČäņäØĒĢ£ļŗż. ņŗżĒŚś Ļ▓░Ļ│╝, DAE ĻĖ░ļ░ś ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØĆ ļŗżļźĖ ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņŚÉ ļ╣äĒĢ┤ ĒāÉņ¦Ć ņä▒ļŖź Ē¢źņāüņŚÉ Ļ░Ćņן ĒÜ©Ļ│╝ņĀüņØĖ Ļ▓āņØä ĒÖĢņØĖĒĢśņśĆļŗż.
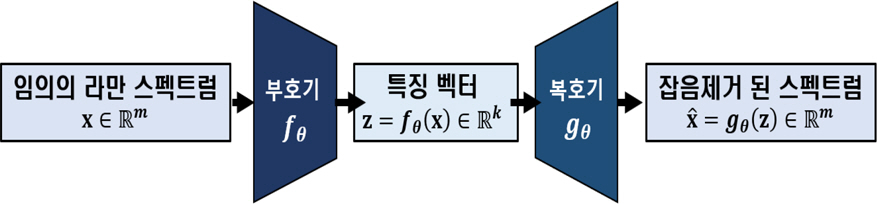
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö ļŗ©ņØ╝ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņĀĢļ│┤ļ¦īņØä ņØ┤ņÜ®ĒĢśņŚ¼ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØś ņ×ĪņØīņØä ņĀ£Ļ▒░ĒĢśĻĖ░ ņ£äĒĢ£ ņĢīĻ│Āļ”¼ņ”śņØä ņäżļ¬ģĒĢ£ļŗż. ļ╣äņĀæņ┤ēņŗØ ļØ╝ļ¦ī ļČäĻ┤æĻ│äļĪ£ ņĖĪņĀĢĒĢ£ NĻ░£ņØś ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│ĖņØä Ļ░Ćņ¦ä ļŹ░ņØ┤Ēä░ņģŗņØ┤ ņ┤Ø C ņóģņØś ĒÖöĒĢÖņ×æņÜ®ņĀ£ļź╝ ĒżĒĢ©ĒĢśĻ│Ā ņ׳ņ£╝ļ®░, Ļ░ü ĒÖöĒĢÖņ×æņÜ®ņĀ£ ļ¦łļŗż N i , ŌĆē i = 0 , ŌĆ” , C ŌĆē - 1 N = Ōłæ i = 0 C - 1 N i x Ōłł R m s Ōłł R + m v Ōłł R m
ņŚ¼ĻĖ░ņä£ ņ×ĪņØī ņŗĀĒśĖ vļź╝ Ļ░ĆņÜ░ņŗ£ņĢł ļ×£ļŹż ļ▓ĪĒä░ v~N(0, Qn)ļØ╝ Ļ░ĆņĀĢĒĢĀ ļĢī, ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņĖĪņĀĢ ņŗĀĒśĖ xļŖö Ļ░ĆņÜ░ņŗ£ņĢł ļ×£ļŹż ļ▓ĪĒä░ x~N(s, Qn)ņØ┤ļŗż. ĻĘĖļ”¼Ļ│Ā Q n Ōłł R m ├Ś m
ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØĆ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņĖĪņĀĢ ņŗĀĒśĖ xļź╝ ņ×ģļĀźļ░øņĢä, ņŗĀĒśĖ xļ│┤ļŗż ļåÆņØĆ ņŗĀĒśĖļīĆņ×ĪņØīļ╣ä(Signal-to-Noise Ratio, SNR)ļź╝ Ļ░Ćņ¦ä ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ŅüŻ x ^ Ōłł R m z = f ╬ś ( x ) Ōłł R k x ^ = g ╬ś ( z )
ĻĖ░ņĪ┤ DAE[12]ļŖö ļŗżņØī ņåÉņŗż ĒĢ©ņłśļź╝ ņĄ£ņåīĒÖöĒĢśļŖö ļ░®Ē¢źņ£╝ļĪ£ ĒĢÖņŖĄĒĢ£ļŗż,
ņŚ¼ĻĖ░ņä£ y Ōłł R m
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ ņĀ£ņĢłĒĢśļŖö DAE ĻĖ░ļ░ś ņ×ĪņØīņĀ£Ļ▒░ ĻĖ░ļ▓ĢņØĆ ņ×ĪņØīņØä Ļ░Ćņ¦ä ļŹ░ņØ┤Ēä░ņģŗņŚÉņä£ ņ×ĪņØīņĀ£Ļ▒░ ĻĖ░ļŖźņØä ĒĢÖņŖĄĒĢśļŖö ļ¼ĖņĀ£ļź╝ ĒĢ┤Ļ▓░ĒĢśĻĖ░ ņ£äĒĢ┤ ļÅÖņØ╝ĒĢ£ ļīĆņāüņŚÉ ļīĆĒĢ┤ ņŚ¼ļ¤¼ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│ĖņØä ņĖĪņĀĢĒĢ£ Ēøä, Ēæ£ļ│Ė Ļ░ä Ļ│ĄĒåĄ ņĀĢļ│┤ļź╝ ĒÖ£ņÜ®ĒĢ£ļŗż. ĻĄ¼ņ▓┤ņĀüņ£╝ļĪ£, ļŹ░ņØ┤Ēä░ņģŗ ļé┤ iļ▓łņ¦Ė ĒÖöĒĢÖņ×æņÜ®ņĀ£ņŚÉ ļīĆĒĢ£ jļ▓łņ¦Ė ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│Ė xi,jņÖĆ ĒĢ┤ļŗ╣ ĒÖöĒĢÖņ×æņÜ®ņĀ£ņØś ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│Ė k-1Ļ░£ļĪ£ ĻĄ¼ņä▒ļÉ£ ņ¦æĒĢ® X i , j ŌĆē = ŌĆē { X i , ŌĆē l ŌĆē Ōłł ŌĆē ŌäØ m | l ŌĆē = j - k - 1 2 + ╬│ , ŌĆē 0 ŌĆē Ōēż ŌĆē ╬│ Ōēż ŌĆē k - 1 , ŌĆē ╬│ ŌĆē Ōłł Ōäż ŌĆē } X ^ i , j ┬Ā = ┬Ā { x ^ i , l ┬Ā Ōłł R m | x ^ i , l = g ╬ś ( f ╬ś ( x i , l ) ) , ┬Ā x i , l Ōłł X i , j }
ņŚ¼ĻĖ░ņä£ N>0 ņØĆ ļŹ░ņØ┤Ēä░ņģŗ ļé┤ Ēæ£ļ│ĖņØś ņ┤Ø Ļ░£ņłśļź╝ ņØśļ»ĖĒĢ£ļŗż. ņāüĻĖ░ ņåÉņŗż ĒĢ©ņłśļĪ£ ņØĖĒĢ┤ DAEļŖö Ļ░ü ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│Ė xi,jļ¦łļŗż ņØĖĻĘ╝ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│ĖļōżņØś ņ¦æĒĢ® Xi,jņŚÉņä£ Ļ│ĄĒåĄņĀüņØĖ ĒŖ╣ņ¦ĢņØä ņČöņĀĢĒĢśļÅäļĪØ ĒĢÖņŖĄĒĢ£ļŗż. ņŚ¼ĻĖ░ņä£ ņåÉņŗż ĒĢ©ņłśļź╝ ĒÅēĻĘĀņĀ£Ļ│▒ņśżņ░©(mean square error)ļĪ£ Ļ│äņé░ĒĢ£ ņØ┤ņ£ĀļŖö ĒÅēĻĘĀņĀłļīĆņśżņ░©(mean absolute error)ļ│┤ļŗż ĒÅēĻĘĀņĀ£Ļ│▒ņśżņ░©Ļ░Ć ņŗżĒŚśņĀüņ£╝ļĪ£ ļŹö ņóŗņØĆ ņä▒ļŖźņØä ļ│┤ņØ┤ĻĖ░ ļĢīļ¼ĖņØ┤ļŗż.
ļśÉ ļŗżļźĖ ļ¼ĖņĀ£ļŖö ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ļŹ░ņØ┤Ēä░ņģŗ ļé┤ ĒÖśĻ▓Į ļŗżņ¢æņä▒ ļ░Å Ēæ£ļ│ĖņØś ņ¢æņØ┤ ņĀ£ĒĢ£ņĀüņØ┤ļØ╝ļŖö Ļ▓āņØ┤ļŗż. ņĀ£ĒĢ£ņĀüņØĖ ĒÖśĻ▓ĮņŚÉņä£ ņĖĪņĀĢĒĢ£ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│Ėļ¦īņ£╝ļĪ£ ņØ╝ļ░śņĀüņØĖ ļŹ░ņØ┤Ēä░ņŚÉ ļīĆĒĢ┤ņä£ļÅä ņ£ĀĒÜ©ĒĢ£ ņ×ĪņØīņĀ£Ļ▒░ ņä▒ļŖźņØä ĒĢÖņŖĄņŗ£ĒéżĻĖ░ ņ£äĒĢ┤ ļŗżņØīĻ│╝ Ļ░ÖņØĆ triplet ņåÉņŗż ĒĢ©ņłś[14] LTripletļź╝ ņĀüņÜ®ĒĢ£ļŗż,
ņŚ¼ĻĖ░ņä£ zj = f╬Ė(xj)ļŖö jļ▓łņ¦Ė ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│Ė xjņŚÉ ļīĆĒĢ£ DAEņØś ĒŖ╣ņ¦Ģ ļ▓ĪĒä░ņØ┤ļŗż. p j Ōłł R k n j Ōłł R k
ņŗØ (3)ņØś ņåÉņŗżĒĢ©ņłśļŖö ļÅÖņØ╝ ĒÖöĒĢÖņ×æņÜ®ņĀ£ņØś ĒŖ╣ņ¦Ģļ▓ĪĒä░ Ļ░ä ņ£ĀĒü┤ļ”¼ļō£ Ļ▒░ļ”¼ļŖö ņĄ£ņåīĒÖöĒĢśĻ│Ā, ņä£ļĪ£ ļŗżļźĖ ĒÖöĒĢÖņ×æņÜ®ņĀ£ņØś ĒŖ╣ņ¦Ģļ▓ĪĒä░ Ļ░ä ņ£ĀĒü┤ļ”¼ļō£ Ļ▒░ļ”¼ļź╝ ņĄ£ļīĆĒÖöĒĢ£ļŗż. ņØ┤ļź╝ ĒåĄĒĢ┤ DAEņØś ļČĆĒśĖĻĖ░ f╬ĖĻ░Ć ņ×ģļĀźļÉ£ ĒÖöĒĢÖņ×æņÜ®ņĀ£ņØś ĒŖ╣ņä▒ņØä ĒŖ╣ņ¦Ģļ▓ĪĒä░ņŚÉ ļ░śņśüĒĢśļÅäļĪØ ņ¦üņĀæņĀüņ£╝ļĪ£ ĒĢÖņŖĄņŗ£Ēé©ļŗż. Ļ▓░Ļ│╝ņĀüņ£╝ļĪ£ ĒĢÖņŖĄ ļŹ░ņØ┤Ēä░ņģŗņŚÉ ņŚåļŖö ĒÖśĻ▓ĮņŚÉņä£ ņĖĪņĀĢĒĢ£ ļØ╝ļ¦ī ņŗĀĒśĖņŚÉ ļīĆĒĢ┤ņä£ļÅä DAEĻ░Ć ņ×ģļĀźļÉ£ ĒÖöĒĢÖņ×æņÜ®ņĀ£ļź╝ ņØĖņ¦ĆĒĢśĻ│Ā, ņ×ĪņØīņØ┤ ņŚåļŖö ĒÖöĒĢÖņ×æņÜ®ņĀ£ņØś ņŖżĒÄÖĒŖĖļ¤╝ņØä ļ│ĄņøÉĒĢĀ ņłś ņ׳ļÅäļĪØ ļ¦īļōĀļŗż. triplet ņåÉņŗż ĒĢ©ņłśņŚÉ ļīĆĒĢ£ ļŹö ņ×ÉņäĖĒĢ£ ņäżļ¬ģņØĆ Ļ┤ĆļĀ© ļģ╝ļ¼Ė[14]ņØä ņ░ĖĻ│ĀĒĢ£ļŗż.
ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ ņĀ£ņĢłĒĢśļŖö DAEļŖö ņŗØ (2)ņÖĆ ņŗØ (3)ņØś ņäĀĒśĢ Ļ▓░ĒĢ®ņ£╝ļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦ä ļŗżņØī ņåÉņŗż ĒĢ©ņłśļĪ£ ĒĢÖņŖĄĒĢ£ļŗż,
ņŚ¼ĻĖ░ņä£ ╬╗ConsistencyņÖĆ ╬╗TripletņØĆ Ļ░ü ņåÉņŗżĒĢ©ņłśņØś Ļ░Ćņżæņ╣śņØ┤ļŗż.
2ņןņŚÉņä£ ņäżļ¬ģĒĢ£ DAE ĻĖ░ļ░ś ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØä ņŗżņĀ£ ņĖĪņĀĢĒĢ£ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ ņĀüņÜ®ĒĢśĻ│Ā ņä▒ļŖźņØä ĒÅēĻ░ĆĒĢ£ļŗż. ņŗżĒŚś ņ×ÉļŻīļŖö ņé╝ņ¢æĒÖöĒĢÖņŚÉņä£ ņĀ£ņ×æĒĢ£ ļ╣äņĀæņ┤ēņŗØ ņ×ÉņÖĖņäĀ ļØ╝ļ¦ī ļČäĻ┤æ ņןļ╣ä KRAMS[2]ļĪ£ ņĖĪņĀĢĒĢ£ļŗż. ņĢäņŖżĒīöĒŖĖ, ņĮśĒü¼ļ”¼ĒŖĖ, ņ£Āļ”¼ ņ┤Ø 3ņóģņØś ļ░░Ļ▓Į ļ¼╝ņ¦ł ņ£äņŚÉ GF(cyclosarin), HN3(nitrogen mustard), MES(mecetronium ethylsulfate) ņ┤Ø 3ņóģņØś ĒÖöĒĢÖņ×æņÜ®ņĀ£ļź╝ ņĢĮ 2 ┬ĄŌäō ļ¦īĒü╝ ļ┐īļ”░ ļŗżņØī 292.92 cm-1 Ōł╝ 3654.98 cm-1ņØś Ēīīņłś ļ▓öņ£äņŚÉņä£ 1024Ļ░£ Ļ░ÆņŚÉ ļīĆĒĢ£ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØä ņĖĪņĀĢĒĢ£ļŗż. Ļ░ü ļ░░Ļ▓Įļ¼╝ņ¦ł ļ░Å ĒÖöĒĢÖņ×æņÜ®ņĀ£ļ¦łļŗż 500Ļ░£ņØś ņŖżĒÄÖĒŖĖļ¤╝ņØä ņĖĪņĀĢĒĢśņŚ¼ ĒĢÖņŖĄ ļŹ░ņØ┤Ēä░ņģŗņØä ĻĄ¼ņä▒ĒĢ£ļŗż. ņØ┤Ēøä, Ļ░ü ļ░░Ļ▓Įļ¼╝ņ¦ł ļ░Å ĒÖöĒĢÖņ×æņÜ®ņĀ£ļ¦łļŗż 100Ļ░£ņØś ņŖżĒÄÖĒŖĖļ¤╝ņØä ņČöĻ░ĆļĪ£ ņĖĪņĀĢĒĢśņŚ¼ ņŗ£ĒŚś ļŹ░ņØ┤Ēä░ņģŗņØä ĻĄ¼ņä▒ĒĢ£ļŗż.
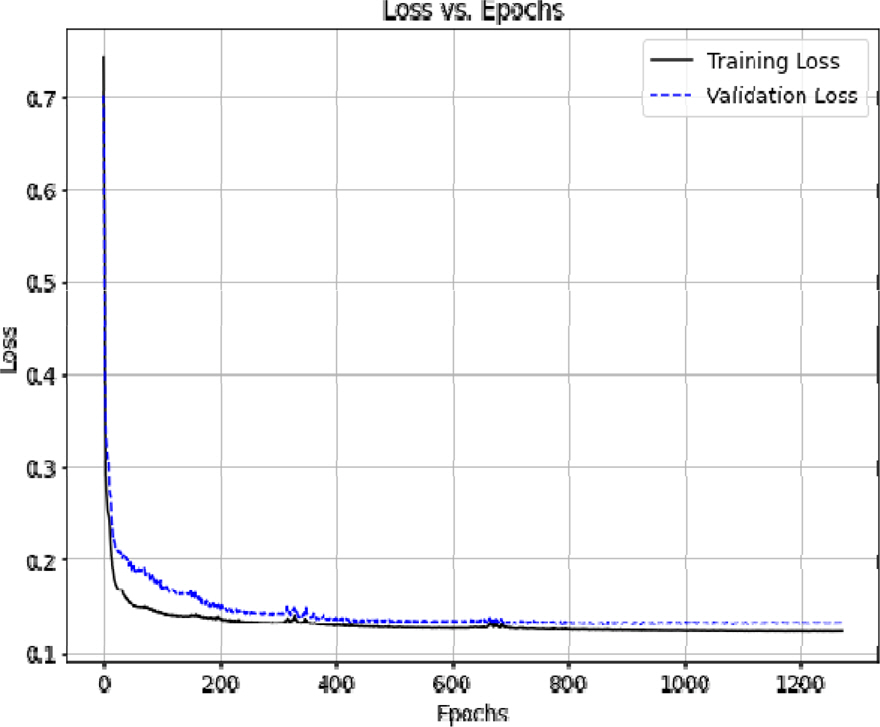
DAEļŖö Ļ░üĻ░ü 3ņĖĄ ņŗĀĻ▓Įļ¦Øņ£╝ļĪ£ ņØ┤ļŻ©ņ¢┤ņ¦ä ļČĆĒśĖĻĖ░ņÖĆ ļ│ĄĒśĖĻĖ░ļĪ£ ĻĄ¼ņä▒ļÉśņ¢┤ ņ׳ņ£╝ļ®░, Ļ░ü ņĖĄņØś ņäżņĀĢņØĆ Table 1Ļ│╝ Ļ░Öļŗż. ņŗØ (2)ņØś ņ£łļÅäņÜ░ Ēü¼ĻĖ░ kļŖö 3ņ£╝ļĪ£ ņäżņĀĢĒĢśņśĆļŗż. ņŚ¼ĻĖ░ņä£ kņØś Ēü¼ĻĖ░ļŖö DAE ņä▒ļŖźņŚÉ Ēü░ ņśüĒ¢źņØä ļ»Ėņ╣śņ¦Ć ņĢŖņ£╝ļ®░, kĻ░Ć ņ╗żņ¦łņłśļĪØ ĒĢÖņŖĄ ņŗ£Ļ░äņØ┤ ļŖśņ¢┤ļé£ļŗż. DAEļŖö ļ░░Ļ▓Įļ¼╝ņ¦ł ļ░Å ĒÖöĒĢÖņ×æņÜ®ņĀ£ļ¦łļŗż 500Ļ░£ņØś ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│ĖņØä ņĖĪņĀĢĒĢśņŚ¼ ĒÖĢļ│┤ĒĢ£ ĒĢÖņŖĄ ļŹ░ņØ┤Ēä░ņģŗņ£╝ļĪ£ ĒĢÖņŖĄĒĢ£ļŗż. GPUļŖö NVIDIA Titan Xļź╝ ņé¼ņÜ®ĒĢśļ®░, ņĮöļō£ļŖö Python3 ĒÖśĻ▓ĮņŚÉņä£ Tensorflowļź╝ ņØ┤ņÜ®ĒĢśņŚ¼ ĻĄ¼ĒśäĒĢ£ļŗż. ņŗØ (3)ņØś ╬▒ļŖö 0.5ļĪ£ ņäżņĀĢĒĢśĻ│Ā, ņŗØ (4)ņØś ╬╗Consistency, ╬╗TripletļŖö 1ļĪ£ ņäżņĀĢĒĢ£ļŗż. ĒĢÖņŖĄļźĀņØĆ 10-3, ņĀĢĻĘ£ĒÖöļŖö L2 ņĀĢĻĘ£ĒÖöņØ┤ļ®░ ņĀĢĻĘ£ĒÖö Ļ│äņłś ╬╗ļŖö 10-6, ļō£ļĪŁņĢäņøā ĒÖĢļźĀņØĆ 0.35ļĪ£ ņäżņĀĢĒĢ£ļŗż. ļśÉĒĢ£ ĒĢÖņŖĄļźĀ ņŖżņ╝ĆņżäņØĆ Stochastic Gradient Descent with Warm Restarts(SGDR)[15]ņØä ņé¼ņÜ®ĒĢśĻ│Ā ņĄ£ņĀüĒÖöĻĖ░ļ▓ĢņØĆ Adaptive moment estimation(Adam)[16]ņØä ņé¼ņÜ®ĒĢ£ļŗż. ņāüĻĖ░ ĒīīļØ╝ļ»ĖĒä░ ņäżņĀĢ ĒĢśņŚÉ ņ┤Ø 1270 epochņØä Ļ▒░ņ│É 30ļČä ļÅÖņĢł ĒĢÖņŖĄņØä ņłśĒ¢ēĒĢśņśĆļŗż. ĒĢÖņŖĄ Ļ│╝ņĀĢ ņżæ ĒĢÖņŖĄ ņåÉņŗż ĒĢ©ņłśņÖĆ Ļ▓Ćņ”Ø ņåÉņŗż ĒĢ©ņłśņØś ļ│ĆĒÖö ĻĘĖļלĒöäļŖö Fig. 2ņÖĆ Ļ░Öļŗż. ĒĢÖņŖĄņØ┤ ņ¦äĒ¢ēļÉ©ņŚÉ ļö░ļØ╝ ĒĢÖņŖĄ ņåÉņŗż ĒĢ©ņłś Ļ░ÆņØ┤ ņĢĮ 0.12ļĪ£ ņłśļĀ┤ĒĢśĻ│Ā Ļ▓Ćņ”Ø ņåÉņŗż ĒĢ©ņłś Ļ░ÆņØĆ 0.13ņ£╝ļĪ£ ņłśļĀ┤ĒĢ£ļŗż.
ĒĢÖņŖĄņØ┤ ņÖäļŻīļÉ£ DAEņØś ņä▒ļŖźņØä ĒÖĢņØĖĒĢśĻĖ░ ņ£äĒĢ┤ ĻĖ░ņĪ┤ņØś ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śĻ│╝ ņä▒ļŖźņØä ļ╣äĻĄÉĒĢ£ļŗż. ļŗ©ņØ╝ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņĀĢļ│┤ļ¦īņ£╝ļĪ£ ņ×ĪņØīņØä ņĀ£Ļ▒░ĒĢśĻĖ░ ņ£äĒĢ┤ ņŚ░ĻĄ¼ļÉ£ ņĢīĻ│Āļ”¼ņ”śņ£╝ļĪ£ļŖö S-G ĒĢäĒä░[5], ĒæĖļ”¼ņŚÉ ļ│ĆĒÖś[7], ņØ┤ļÅÖ ĒÅēĻĘĀ[8], ņżæĻ░äĻ░Æ ĒĢäĒä░[9]Ļ░Ć ņ׳ļŗż.
S-G ĒĢäĒä░(Savitzky-Golay filter, S-G filter) ĻĖ░ļ░ś ņ×ĪņØīņĀ£Ļ▒░ ĻĖ░ļ▓ĢņØĆ ņŖżĒÄÖĒŖĖļ¤╝ ļé┤ņØś ĒĢ£ ņĀÉņØä ĻĖ░ņżĆņ£╝ļĪ£ ņØĖĻĘ╝ kĻ░£ņØś ņĀÉņØä ņäĀĒāØĒĢśĻ│Ā, ņØ┤ļź╝ ĻĘ╝ņé¼ĒĢśļŖö nņ░© ļŗżĒĢŁņŗØņØä ņ░ŠņØīņ£╝ļĪ£ņŹ© ņ×ĪņØī ņä▒ļČäņØ┤ ņĀ£Ļ▒░ļÉ£ ņŖżĒÄÖĒŖĖļ¤╝ Ļ░ÆņØä ņČöņĀĢĒĢ£ļŗż[5]. ņ£łļÅäņÜ░ņŚÉ ļōżņ¢┤Ļ░ł ņŖżĒÄÖĒŖĖļ¤╝ Ļ░ÆņØś Ļ░£ņłś kņÖĆ ļŗżĒĢŁņŗØ ņ░©ņłś nņØä ņØ┤ņÜ®ĒĢśņŚ¼ Ļ│äņłśĒ¢ēļĀ¼ MņØä Ļ│äņé░ĒĢĀ ņłś ņ׳Ļ│Ā, ņŖ¼ļØ╝ņØ┤ļö® ņ£łļÅäņÜ░(sliding window) ļ░®ņŗØņ£╝ļĪ£ ļ¬©ļōĀ ņŖżĒÄÖĒŖĖļ¤╝ Ļ░ÆņŚÉ ļīĆĒĢ┤ Ļ│äņłśĒ¢ēļĀ¼ MĻ│╝ ĒĢ®ņä▒Ļ│▒(convolution) ņŚ░ņé░ņØä ņĀüņÜ®ĒĢ©ņ£╝ļĪ£ņŹ© ņ×ĪņØīņØ┤ ņĀ£Ļ▒░ļÉ£ ņŖżĒÄÖĒŖĖļ¤╝ X ^
ĒæĖļ”¼ņŚÉ ļ│ĆĒÖś(Fourier Transform, FT) ĻĖ░ļ░ś ņ×ĪņØīņĀ£Ļ▒░ ĻĖ░ļ▓ĢņØĆ ņØ╝ļ░śņĀüņ£╝ļĪ£ ļ×£ļŹż ņ×ĪņØīņŚÉņä£ Ļ│ĀņŻ╝Ēīīņłś ņä▒ļČäņØ┤ ņŗĀĒśĖņŚÉ ņśüĒ¢źņØä ļ¦ÄņØ┤ ņżĆļŗżļŖö ĒŖ╣ņ¦ĢņØä ĻĖ░ļ░śņ£╝ļĪ£, ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņŚÉ Ļ│ĀņåŹ ĒæĖļ”¼ņŚÉ ļ│ĆĒÖśņØä ņĀüņÜ®ĒĢśņŚ¼ ņŻ╝Ēīīņłś ņśüņŚŁņŚÉņä£ Ēæ£ĒśäĒĢ£ Ēøä, kĻ░£ņØś ņĀĆņŻ╝Ēīīņłś ņä▒ļČäņØä ņĘ©ĒĢśĻ│Ā Ļ│ĀņåŹ ĒæĖļ”¼ņŚÉ ņŚŁļ│ĆĒÖśņØä ņĀüņÜ®ĒĢśņŚ¼ ņ×ĪņØīņØ┤ ņĀ£Ļ▒░ļÉ£ ņŖżĒÄÖĒŖĖļ¤╝ X ^
ņØ┤ļÅÖ ĒÅēĻĘĀ(Moving Average, MA) ĻĖ░ļ░ś ņ×ĪņØīņĀ£Ļ▒░ ĻĖ░ļ▓ĢņØĆ ņŖżĒÄÖĒŖĖļ¤╝ ļé┤ņØś ĒĢ£ ņĀÉņØä ĻĖ░ņżĆņ£╝ļĪ£ ņØĖĻĘ╝ kĻ░£ņØś ņĀÉņØä ņäĀĒāØĒĢśĻ│Ā, ĒĢ┤ļŗ╣ ņĀÉļōżņØś ĒÅēĻĘĀĻ░ÆņØä Ļ│äņé░ĒĢśņŚ¼ ņ×ĪņØī ņä▒ļČäņØ┤ ņĀ£Ļ▒░ļÉ£ ņŖżĒÄÖĒŖĖļ¤╝ Ļ░ÆņØä ņČöņĀĢĒĢ£ļŗż[8]. ņŖ¼ļØ╝ņØ┤ļö® ņ£łļÅäņÜ░ ļ░®ņŗØņ£╝ļĪ£ ļ¬©ļōĀ ņŖżĒÄÖĒŖĖļ¤╝ Ļ░ÆņŚÉ ļīĆĒĢ┤ ņ£łļÅäņÜ░ ļé┤ ĒÅēĻĘĀĻ░ÆņØä Ļ│äņé░ĒĢśņŚ¼ ņ×ĪņØīņØ┤ ņĀ£Ļ▒░ļÉ£ ņŖżĒÄÖĒŖĖļ¤╝ ŅüŻ X ^
ņżæĻ░äĻ░Æ ĒĢäĒä░(Median Filter, MF) ĻĖ░ļ░ś ņ×ĪņØīņĀ£Ļ▒░ ĻĖ░ļ▓ĢņØĆ ņŖżĒÄÖĒŖĖļ¤╝ ļé┤ņØś ĒĢ£ ņĀÉņØä ĻĖ░ņżĆņ£╝ļĪ£ ņØĖĻĘ╝ kĻ░£ņØś ņĀÉņØä ņäĀĒāØĒĢśĻ│Ā, ĒĢ┤ļŗ╣ ņĀÉļōżņØś ņżæĻ░äĻ░ÆņØä Ļ│äņé░ĒĢśņŚ¼ ņ×ĪņØī ņä▒ļČäņØ┤ ņĀ£Ļ▒░ļÉ£ ņŖżĒÄÖĒŖĖļ¤╝ Ļ░ÆņØä ņČöņĀĢĒĢ£ļŗż[9]. ņŖ¼ļØ╝ņØ┤ļö® ņ£łļÅäņÜ░ ļ░®ņŗØņ£╝ļĪ£ ļ¬©ļōĀ ņŖżĒÄÖĒŖĖļ¤╝ Ļ░ÆņŚÉ ļīĆĒĢ┤ ņ£łļÅäņÜ░ ļé┤ ņżæĻ░äĻ░ÆņØä Ļ│äņé░ĒĢśņŚ¼ ņ×ĪņØīņØ┤ ņĀ£Ļ▒░ļÉ£ ņŖżĒÄÖĒŖĖļ¤╝ X ^
ņĀĢļ”¼ĒĢśļ®┤, ļ│Ė ļģ╝ļ¼ĖņŚÉņä£ļŖö Ļ░ü ļ░░Ļ▓Įļ¼╝ņ¦ł ļ░Å ĒÖöĒĢÖņ×æņÜ®ņĀ£ļ¦łļŗż 100Ļ░£ņØś ņŖżĒÄÖĒŖĖļ¤╝ņØä ņĖĪņĀĢĒĢ£ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņŗ£ĒŚś ļŹ░ņØ┤Ēä░ņģŗņØä ņØ┤ņÜ®ĒĢśņŚ¼ ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØä ņĀüņÜ®ĒĢśņ¦Ć ņĢŖņØĆ Ļ▓ĮņÜ░ņØĖ RawņÖĆ ĒĢ©Ļ╗ś S-G filter, FT, MA, MF, DAE (C), DAE (CT) 6Ļ░£ņØś ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØä ņĀüņÜ®ĒĢ£ Ļ▓ĮņÜ░ļź╝ ĒĢ®ņ│É ņ┤Ø 7Ļ░£ņØś Ļ▓ĮņÜ░ņŚÉ ļīĆĒĢ┤ ņŗĀĒśĖ ĒŖ╣ņä▒ ļ░Å ņ×æņÜ®ņĀ£ ĒāÉņ¦Ć ņä▒ļŖźņØä ĒÖĢņØĖĒĢ£ļŗż. ņŚ¼ĻĖ░ņä£ DAE (C)ļŖö ņŗØ (2)ņØś ņåÉņŗż ĒĢ©ņłś LConsistencyļ¦īņ£╝ļĪ£ ĒĢÖņŖĄĒĢ£ DAEļź╝ ņØśļ»ĖĒĢśĻ│Ā, DAE (CT)ļŖö ņŗØ (4)ļź╝ ļö░ļØ╝ LConsistencyņÖĆ LTriplet ļ¬©ļæÉ ņØ┤ņÜ®ĒĢśņŚ¼ ĒĢÖņŖĄĒĢ£ DAEļź╝ ņØśļ»ĖĒĢ£ļŗż. ļæÉ Ļ░Ćņ¦Ć Ļ▓ĮņÜ░ņŚÉ ļīĆĒĢ┤ DAEņØś ņä▒ļŖźņØä ļ╣äĻĄÉĒĢ©ņ£╝ļĪ£ņŹ© ņŗØ (3) ņåÉņŗż ĒĢ©ņłś LTripletņØś ĒÜ©Ļ│╝ļź╝ ĒÖĢņØĖĒĢ£ļŗż. ņØ┤ļĢī Ļ░ü ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”ś ļ│ä ĒīīļØ╝ļ»ĖĒä░ļŖö ļŗżņØī Table 2ņÖĆ Ļ░ÖņØ┤ ņäżņĀĢĒĢ£ļŗż.
ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØś ņ×ĪņØīņĀ£Ļ▒░ ņä▒ļŖźņØä ļ╣äĻĄÉĒĢśĻĖ░ ņ£äĒĢ┤ ļ©╝ņĀĆ ņ×ĪņØīņĀ£Ļ▒░ ņĀä/Ēøä ņŖżĒÄÖĒŖĖļ¤╝ņØś ĒśĢĒā£ļź╝ ļ╣äĻĄÉĒĢ£ļŗż. ļ╣äĻĄÉ ļīĆņāüņ£╝ļĪ£ ņé¼ņÜ®ĒĢśļŖö ĒÖöĒĢÖņ×æņÜ®ņĀ£ļŖö ņŗĀĻ▓Į ĒÖöĒĢÖņ×æņÜ®ņĀ£ņØś ņØ╝ņóģņØĖ GFņØ┤ļŗż. GFņØś ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØĆ 458 Ōł╝ 1705 cm-1 ļīĆņŚŁĻ│╝ 2626 Ōł╝ 3093 cm-1 ļīĆņŚŁņŚÉ ĒŖ╣ņ¦Ģ ĒīīĒśĢņØä ļ│┤ņ£ĀĒĢśĻ│Ā ņ׳ļŗż. Fig. 3ņØĆ ņĢäņŖżĒīöĒŖĖ ļ░░Ļ▓ĮņŚÉ ļīĆĒĢ┤ ņĖĪņĀĢĒĢ£ GF ņ×æņÜ®ņĀ£ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│ĖĻ│╝ Ļ░ü ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”ś ņĀüņÜ® Ļ▓░Ļ│╝ļź╝ ļ│┤ņŚ¼ņżĆļŗż. Fig. 3 (a)ļŖö ņĢäņŖżĒīöĒŖĖ ļ░░Ļ▓Į ņ£ä GF ņ×æņÜ®ņĀ£ņØś ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØä ņĖĪņĀĢĒĢ£ Ēæ£ļ│ĖņØ┤ļŗż. Fig. 3 (b) Ōł╝ (g)ļŖö Ļ░ü ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØä ņĀüņÜ®ĒĢśņŚ¼ ĒÜŹļōØĒĢ£ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ņØ┤ļŗż. Fig. 3 (a)ņØś ņŖżĒÄÖĒŖĖļ¤╝ ĒśĢĒā£ņÖĆ Fig. 3 (b) Ōł╝ (g)ņØś ņ×ĪņØīņØ┤ ņĀ£Ļ▒░ļÉ£ ņŖżĒÄÖĒŖĖļ¤╝ ĒśĢĒā£ļź╝ ļ╣äĻĄÉĒĢśļ®┤ ņŖżĒÄÖĒŖĖļ¤╝ Ļ░ÆņØś ļČäņé░ņØ┤ Ļ░ÉņåīĒĢ£ Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. Fig. 3 (a) Ōł╝ (g) ņżæņŚÉņä£ ņŖżĒÄÖĒŖĖļ¤╝ Ļ░ÆņØś ļČäņé░ņØ┤ ņĀ£ņØ╝ ņ×æņØĆ Ļ▓āņØĆ Fig. 3 (f) Ōł╝ (g)ņØś DAE (C)ņÖĆ DAE (CT)ļĪ£ ņ×ĪņØīņØ┤ ņĀ£Ļ▒░ļÉ£ ļØ╝ļ¦ī ņŗĀĒśĖņØ┤ļŗż.
Ļ░ü ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØ┤ ĒÖöĒĢÖņ×æņÜ®ņĀ£ ĒāÉņ¦Ć ņä▒ļŖźņŚÉ ļ»Ėņ╣śļŖö ņśüĒ¢źņØä ĒÅēĻ░ĆĒĢśĻĖ░ ņ£äĒĢ┤ ņØ╝ļ░ś ņÜ░ļÅäļ╣ä Ļ▓ĆņĀĢ(Generalized Likelihood Ratio Test, GLRT)[17] ĒāÉņ¦Ć ņĢīĻ│Āļ”¼ņ”śņØä ņé¼ņÜ®ĒĢśĻ│Ā, ņĀäņ▓┤ ņĀĢĒÖĢļÅä(Overall Accuracy, OA)ļź╝ ņé¼ņÜ®ĒĢ£ļŗż.
ĒāÉņ¦Ć ņĢīĻ│Āļ”¼ņ”śņØĖ GLRTļŖö ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ x ļź╝ ņäĀĒśĢ ļČĆļČäĻ│ĄĻ░ä ļ¬©ļŹĖ[11]ļĪ£ Ļ░ĆņĀĢĒĢ£ Ēøä, Ļ▓ĆņĀĢĒåĄĻ│ä T(X)ļź╝ ļŗżņØī ņŗØņØä ļö░ļØ╝ Ļ│äņé░ĒĢ£ļŗż.
ņŚ¼ĻĖ░ņä£ ņ¦üĻĄÉ Ēł¼ņśü Ē¢ēļĀ¼ P 1 K Ōłł R m ├Ś m , ┬Ā P 1 K b g Ōłł R m ├Ś m P 1 K = I - K ( K T K ) - 1 K , ┬Ā P 1 K b g = I - K b g ( K b g T K b g ) - 1 K b g K Ōłł R m ├Ś ( C + B ) K b g Ōłł R m ├Ś B
ĒāÉņ¦Ć ņä▒ļŖźņ¦ĆĒæ£ņØĖ OAļŖö ļ¬©ļōĀ ņóģļźśņØś ĒÖöĒĢÖņ×æņÜ®ņĀ£ņŚÉ ļīĆĒĢ£ ĒāÉņ¦Ć ņĀĢĒÖĢļÅäļź╝ ņØśļ»ĖĒĢśļ®░, ļŗżņØīĻ│╝ Ļ░ÖņØ┤ Ļ│äņé░ĒĢ£ļŗż.
ņŚ¼ĻĖ░ņä£ hjŌłł{0, 1}ļŖö jļ▓łņ¦Ė ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│ĖņØ┤ ņ×æņÜ®ņĀ£ņØĖņ¦Ć ņĢäļŗīņ¦Ć ļéśĒāĆļé┤ļŖö ņ░ĖĻ░ÆņØ┤ļ®░, h ^ j Ōłł { 0 , ┬Ā 1 }
Table 3ņØĆ ļ¬©ļōĀ ĒÖöĒĢÖņ×æņÜ®ņĀ£ņŚÉ ļīĆĒĢ┤ Ļ░ü ļ░░Ļ▓Į ļ¼╝ņ¦łļ¦łļŗż GLRTņŚÉ ļīĆĒĢ£ ĒāÉņ¦Ć ņä▒ļŖźņ¦ĆĒæ£ Ļ│äņé░ Ļ▓░Ļ│╝ļź╝ ļ│┤ņŚ¼ņżĆļŗż. ņ¢┤ļ¢ĀĒĢ£ ļ░░Ļ▓ĮņŚÉņä£ļÅä ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØä ņĀüņÜ®ĒĢśļ®┤ ĒāÉņ¦Ć ņä▒ļŖźņØ┤ Rawļ│┤ļŗż Ē¢źņāüļÉśļŖö Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż. ĒŖ╣Ē׳ DAE (CT)ļŖö ļ¬©ļōĀ ĒāÉņ¦Ć ņä▒ļŖźņ¦ĆĒæ£ņŚÉņä£ ļŗżļźĖ ņĢīĻ│Āļ”¼ņ”śļ│┤ļŗż Ēø©ņö¼ Ē¢źņāüļÉ£ ņłśņ╣śļź╝ ļ│┤ņØĖļŗż. ņŗØ (2)ņØś ņåÉņŗż ĒĢ©ņłś LConsistencyļ¦ī ņĀüņÜ®ĒĢ£ DAE (C)ļÅä ĻĖ░ņĪ┤ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņŚÉ ļ╣äĒĢ┤ ļåÆņØĆ ņä▒ļŖź ņłśņ╣śļź╝ ļ│┤ņØ┤ņ¦Ćļ¦ī, ņŗØ (3)ņØś ņåÉņŗż ĒĢ©ņłś LTripletĻ╣īņ¦Ć ņĀüņÜ®ĒĢ£ DAE (CT)ļ│┤ļŗżļŖö ļé«ņØĆ ņä▒ļŖź ņłśņ╣śļź╝ ļ│┤ņØĖļŗż.
ļ│Ė ņŗżĒŚśņŚÉņä£ļŖö ĒĢÖņŖĄņ×ÉļŻī Ļ░£ņłśņŚÉ ļö░ļźĖ DAE ņä▒ļŖźļ│ĆĒÖöļź╝ ĒÖĢņØĖĒĢ©ņ£╝ļĪ£ņŹ© ņåÉņŗż ĒĢ©ņłś LTripletņØś ĒÜ©Ļ│╝ļź╝ ĒÖĢņØĖĒĢ£ļŗż. Fig. 4ļŖö ĒĢÖņŖĄ ļŹ░ņØ┤Ēä░ņģŗ ļé┤ Ļ░ü ņ×æņÜ®ņĀ£ ļŗ╣ ņŖżĒÄÖĒŖĖļ¤╝ Ēæ£ļ│ĖņØś Ļ░£ņłśļź╝ ļ│ĆĒÖöņŗ£Ēéżļ®┤ņä£ DAEļź╝ ĒĢÖņŖĄņŗ£ĒéżĻ│Ā, GLRT ĒāÉņ¦Ć ņĀĢĒÖĢļÅäļź╝ ļ╣äĻĄÉĒĢ£ Ļ▓░Ļ│╝ņØ┤ļŗż. ņ×æņÜ®ņĀ£ ļŗ╣ 100Ōł╝500Ļ░£ņØś ĒĢÖņŖĄņ×ÉļŻīļź╝ ņé¼ņÜ®ĒĢĀ ļĢīņŚÉļŖö ĒĢÖņŖĄņ×ÉļŻī Ļ░£ņłśĻ░Ć ļŖśņ¢┤ļé©ņŚÉ ļö░ļØ╝ ņä▒ļŖź Ē¢źņāüņØä ļ│┤ņØ┤ļ®░, ņØ┤ļĢī DAE (CT)ņØś ņä▒ļŖźņłśņ╣śĻ░Ć DAE (C)ļ│┤ļŗż ļåÆņØĆ Ļ▓āņØä ĒÖĢņØĖĒĢĀ ņłś ņ׳ļŗż.
ļ│Ė ļģ╝ļ¼ĖņØĆ ļŗ©ņØ╝ ņČ£ļĀź ļĀłņØ┤ņĀĆļ¦ī ļ│┤ņ£ĀĒĢ£ ņĀ£ĒĢ£ņĀüņØĖ ņāüĒÖ®ņŚÉņä£ ļ╣äņĀæņ┤ēņŗØ ļØ╝ļ¦ī ļČäĻ┤æĻ│ä ņŗ£ņŖżĒģ£ņØä ņ£äĒĢ£ denoising autoencoder ĻĖ░ļ░ś ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØä ņĀ£ņĢłĒĢ£ļŗż. ņØ┤ļź╝ ņ£äĒĢ┤ ļŹ░ņØ┤Ēä░ņģŗ ļé┤ Ēæ£ļ│Ė Ļ░ä Ļ│ĄĒåĄ ņĀĢļ│┤ļź╝ ĒÖ£ņÜ®ĒĢśĻ│Ā, ļ®öĒŖĖļ”Ł ļ¤¼ļŗØ ĻĖ░ļ▓ĢņØä ņĀüņÜ®ĒĢśņŚ¼ Ēæ£ļ│ĖņØ┤ ņĀ£ĒĢ£ņĀüņØĖ ļŹ░ņØ┤Ēä░ņģŗņØä ĒÜ©ņ£©ņĀüņ£╝ļĪ£ ĒÖ£ņÜ®ĒĢśĻĖ░ ņ£äĒĢ£ ņåÉņŗż ĒĢ©ņłśļź╝ ņĀ£ņĢłĒĢ£ļŗż. ņŗżĒŚśņØä ĒåĄĒĢ┤ denoising autoencoder ĻĖ░ļ░ś ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śĻ│╝ ĻĖ░ņĪ┤ ļØ╝ļ¦ī ņŖżĒÄÖĒŖĖļ¤╝ ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”śņØĖ Savitzky-Golay filter, Fourier transform, moving average, median filter Ļ░ä ļ╣äĻĄÉļź╝ ņłśĒ¢ēĒĢ£ļŗż. ņŗżĒŚś Ļ▓░Ļ│╝, ļ╣äĻĄÉ ļīĆņāü ņ×ĪņØīņĀ£Ļ▒░ ņĢīĻ│Āļ”¼ņ”ś ņżæ ņĀ£ņĢłĒĢ£ ņåÉņŗż ĒĢ©ņłśļĪ£ ĒĢÖņŖĄĒĢ£ denoising autoencoderĻ░Ć ĒÖöĒĢÖņ×æņÜ®ņĀ£ ĒāÉņ¦Ć ņä▒ļŖź Ē¢źņāüņŚÉ ņĀ£ņØ╝ ĒÜ©Ļ│╝ņĀüņØĖ Ļ▓āņ£╝ļĪ£ ļéśĒāĆļé£ļŗż.
References
[1] A. W. Fountain 3 et al, Long Range Standoff Detection of Chemical, Biological and Explosive Hazards on Surfaces, Proc. SPIE 7679, Micro- and Nanotechnology Sensors, Systems, and Applications II, 76790H. 2010.
[2] Y. C. Ha, J. H. Lee, Y. J. Koh, S. K. Lee and Y. K. Kim, "Development of an Ultraviolet Raman Spectrometer for Standoff Detection of Chemicals," Current Optics and Photonics, Vol. 1, No. 3, pp. 247ŌĆō251, 2017.
[3] S. Wallin et al, "Laser-based Standoff Detection of Explosives: A Critical Review," Analytical and Bioanalytical Chemistry, Vol. 395, pp. 259ŌĆō274, 2009.


[4] P. L. Ponsardin et al, Expanding Applications for Surfacecontaminant Sensing Using the Laser Interrogation of Surface Agents(LISA) Technique, Proc. SPIE 5268, Chemical and Biological Standoff Detection. 2004.
[5] S. J. Barton, T. E. Ward and B. M. Hennelly, "Algorithm for Optimal Denoising of Raman Spectra," Analytical Methods, Vol. 10, pp. 3759ŌĆō3769, 2018.

[6] J. Smulko, M. S. Wrobel and I. Barman, Noise in Biological Raman Spectroscopy, 2015 International Conference on Noise and Fluctuations(ICNF). 2015.
[7] P. A. Mosier-Boss, S. H. Lieberman and R. Newbery, "Fluorescence Rejection in Raman Spectroscopy by Shifted-Spectra, Edge Detection, and FFT Filtering Techniques," Applied Spectroscopy, Vol. 49, No. 5, pp. 630ŌĆō638, 1995.

[8] C. C. Soberon-Celedon et al, "Removal of Fluorescence and Shot Noises in Raman Spectra of Biological Samples Using Morphological and Moving Averages Filters," International Journal of Engineering and Technical Research, Vol. 6, No. 3, pp. 2454ŌĆō4698, 2016.
[9] X. Wang et al, "Development of Weak Signal Recognition and an Extraction Algorithm for Raman Imaging," Analytic Chemistry, Vol. 91, No. 20, pp. 12909ŌĆō12916, 2019.

[10] B. Rasti, P. Scheunders, P. Ghamisi, G. Licciardi and J. Chanussot, "Noise Reduction in Hyperspectral Imagery: Overview and Application," Remote Sensing, Vol. 10, No. 3, pp. 4822018.

[11] H.-G. Yu, J. H. Park, C. S. Lee, D.-J. Park, D. E. Chang, H. Nam and B. H. Park, Performance Analysis of the Denoising Algorithms for Detection of Chemical Warfare Agents with Raman Spectroscopy, KIMST Annual Conference Proceedings. pp. 284ŌĆō285, 2020.
[12] C. C. Horgan et al, High-Throughput Molecular Imaging via Deep Learning Enabled Raman Spectroscopy, arxiv:2009.13318. 2020.
[13] X. Lu et al, Speech Enhancement based on Deep Denoising Autoencoder, INTERSPEECH. 2013.
[14] F. Schroff, D. Kalenichenko and J. Philbin, FaceNet: A Unified Embedding for Face Recognition and Clustering, Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. pp. 815ŌĆō823, 2015.
[15] I. Loshchilov and F. Hutter, SGDR: Stochastic Gradient Descent with Warm Restarts, International Conference on Learning Representations. 2017.
[16] D. P. Kingma and J. Ba, Adam: A Method for Stochastic Optimization, International Conference on Learning Representations(ICLR). 2015.
- TOOLS
-
METRICS

-
- 1 Crossref
- 1,989 View
- 66 Download
- Related articles in J. KIMS Technol.