서 론
고정익 항공기에 비해 헬리콥터는 수직 이착륙 및 제자리 비행이 가능하지만 최대 전진 비행 속도가 150∼170 knots 정도로 느리다는 단점이 있다. 따라서 이와 같은 문제를 해결하기 위해 기존의 로터뿐만 아니라 보조 추진 장치와 날개 등을 함께 이용한 복합형 회전익기(compound rotorcraft)가 최근 연구 및 개발되고 있다. 다양한 복합형 회전익기 개념 중 하나인 Lift-offset 복합형 회전익기(Fig. 1)는 ABC(Advancing Blade Concept[1])을 사용한 강체 동축 반전 로터(rigid coaxial rotor 혹은 lift-offset rotor)와 보조 추력 장치를 함께 사용하여 기존 헬리콥터의 장점을 유지하면서 고속 비행을 구현한다.
Lift-offset 로터는 동축반전 로터의 각각의 전진면(advancing side)에서만 양력을 발생하므로(Fig. 2) 일반 헬리콥터의 로터 시스템과는 다르게 후퇴면(retreating side)의 동적 실속(dynamic stall)을 겪지 않는다. 또한, 로터 허브의 롤링 모멘트 트림(trim)이 자동적으로 만족되므로 기존의 헬리콥터 로터에 비하여 로터 전진면에서의 양력을 더욱 크게 만들 수 있다. 로터 회전 속도를 적절히 감속하여 로터 전진면의 압축성 효과를 완화시킬 수 있다는 장점이 있으므로 동시에 보조 추력 장치를 사용하여 고속 비행을 구현할 수 있다. 그러나 Lift-offset 복합형 회전익기는 강성이 매우 큰 블레이드(rigid blade)를 사용하므로 고속 비행 시 극심한 진동을 겪으며 이는 최대 비행 속도를 제한하며, 다양한 구조적 문제를 야기한다[2].
본 논문에서는 머지않은 미래의 전장에서 투입될 수 있는 Lift-offset 로터를 이용하는 고속 비행 복합형 무인 회전익기인 HCUR(High-speed Compound Unmanned Rotorcraft, Fig. 3)에 대하여 Lift-offset 로터의 허브 진동 하중 성분과 기체 진동 응답 사이의 상관 관계를 수치해석 기법을 이용하여 연구한다. HCUR은 Lift-offset 동축반전 로터, 날개, 및 2개의 프로펠러를 함께 사용하는 5000 lb 급의 무인 복합형 회전익기이다[2].
Lift-offset 동축반전 로터는 고유의 특성(inter-rotor cancellation)으로 인하여 이론적으로는 로터 허브의 6개의 진동 하중 성분 중 3개의 진동 하중 성분만 기체를 가진한다[1]. HCUR과 같이 상/하 로터 블레이드가 로터 방위각(azimuth angle, ψ) = 0°에서 교차하는 경우 로터 허브의 수직 축(z-축) 방향 및 기체 축(x-축) 방향의 힘과 y축에 대한 허브 피치 모멘트의 진동 하중 성분만 존재한다[4]. 로터 당 2개의 블레이드(Nb = 2)를 이용하는 HCUR은 로터 회전 속도의 2배의 허브 진동 성분(2/rev = 2P)이 가장 지배적이므로 2P 성분의 Fx, Fz, 및 My의 허브 진동 하중이 가장 중요하다. 고속 비행 시 HCUR 기체의 극심한 진동을 효과적으로 감소 및 제어하기 위하여서는 3개의 로터 허브 진동 하중 성분과 기체 진동 응답 사이의 상관 관계의 이해가 필요하다. 그러나 이와 같은 연구는 참고문헌[5]를 제외하고는 수행된 바가 없으며, 선행연구[5]에서는 로터 허브 진동 하중 성분과 기체 진동 응답 사이의 상관 관계가 일부 제시되어 있으나 모델링 및 해석 기법이 상세하고 체계적으로 서술되어있지 않다[5].
본 연구의 HCUR의 2P 로터 허브 진동 하중은 회전익기 통합 해석 코드(rotorcraft comprehensive analysis code)인 CAMRAD II[6]를 이용한 선행연구[2]로부터 얻 었으며, HCUR 기체는 유한요소 해석 프로그램인 MSC.NASTRAN을 이용하여 1차원 stick 모델로 단순화 및 모델링하였다. 70∼250 knots의 비행 속도에서의 2P 로터 허브 진동 하중이 HCUR 기체를 가진 할 때, 기체 주요 위치(원격 조종 장치, 동체-샤프트 연결부, 날개의 뿌리 및 끝단)에서의 2P의 수직 및 기체 축 방향의 기체 진동 응답을 MSC.NASTRAN을 이용하여 계산하였다. 이때, 3종류의 2P 로터 허브 진동 하중 성분(Fx2P, Fz2P, 및 My2P) 중 기체 진동 응답에 가장 지배적인 영향을 미치는 성분을 조사하였다.
연구 방법
2.1 고속 비행 복합형 무인 회전익기(HCUR)
본 논문의 HCUR 기체의 제원을 Table 1에 정리하였다. 본 논문에 사용된 HCUR Lift-offset 로터에 대한 보다 자세한 설명은 참고문헌[2,7]에 주어져 있다. HCUR의 프로펠러는 축 대칭 유동 조건에서 운용되므로 기체의 가진에 큰 역할을 하지 않기 때문에 기체의 진동은 대부분 Lift-offset 로터 진동 하중으로부터 발생된다. HCUR Lift-offset 로터의 2P 허브 진동 하중은 CAMRAD II를 이용한 선행연구[2]로부터 얻었다.
Table 1.
General properties of HCUR
2.2 HCUR 기체의 유한요소 모델링 기법
HCUR 기체의 구조 동역학 모델링 및 진동 응답 해석을 수행하기 위하여 상용 유한요소 해석 프로그램인 MSC.NASTRAN을 사용하였다. HCUR 기체의 구조 동역학 모델링은 탄성보 요소(CBAR)를 사용하여 1차원(1D) stick 모델로 나타내었다. 1D stick 모델링은 적은 자유도를 사용함에도 3D 기체 구조 모델과 유사한 동특성을 구현 가능하고 3D 구조 모델에 비해 해석 시간이 짧다는 장점이 있다[8]. 본 연구에서는 정규 모드(normal mode) 해석 모델 및 지상 진동 시험(Ground Vibration Test, GVT) 모델의 두 종류의 stick 모델을 이용한다. 기체의 주요 구성 요소들의 중량 정보는 개념 설계 결과로부터 얻으며, 이를 집중 질량 요소(CONM2)로 모델링한다. 이후, UH-60A, XH-59A, 및 XV-15 등의 기존의 회전익기 기체의 모드 특성과 유사할 수 있도록 탄성보 요소(CBAR)의 기하학적 형상 및 재료 물성치의 값을 적절히 가정 및 입력하여 자유(free-free) 경계 조건의 정규 모드 해석용 기체 모델을 구축한다. 이 때, 본 논문에서는 동체와 날개의 진동 응답을 주로 조사하므로 수평 및 수직 꼬리 날개는 간단하게 집중 질량 요소로 나타내었다. 이와 같은 과정으로 얻어진 기체의 정규 모드 해석 모델은 지상 진동 시험 모델의 기준 모델(reference model)로 이용된다.
적절히 모델링된 정규 모드 해석용 기체 stick 모델의 로터 허브 및 꼬리 날개의 위치에 총 2개의 번지 케이블(bungee cable)을 각각 추가하여 지상 진동 시험 모델을 구축한다(Fig. 5). GVT 모델을 이용한 기체 진동 응답 해석 기법은 실제 항공기에 대한 지상 진동 시험 기법과 동일하며, 자유 경계 조건의 로터-기체의 연계 해석 모델(coupled analysis model)에 대한 트림 해석을 수행하지 않으므로 해석이 간편하다는 장점이 있다[9]. 번지 케이블은 1차원 탄성보 요소(CBAR)로 나타내며, 앞서 구축된 자유 경계 조건의 stick 모델의 정규 모드 해석의 고유 진동수 값과 GVT 모델에 대한 주파수 응답 해석(frequency response analysis)의 고유 진동수 값의 오차가 5 % 내로 표현되고 6개의 강체 모드가 얻어지도록 번지 케이블의 길이, 탄성보 요소의 재료 물성치 및 기하학적 형상을 모델링한다.
HCUR 기체의 정규 모드 해석 모델 및 GVT 모델의 고유진동수 해석 결과를 Table 2에 나타내었다. 표에 서 보듯이, 두 해석 모델의 저차 모드 고유 진동수가 5 % 이내의 차이로 상당히 유사함을 알 수 있으며, 따라서 GVT 모델이 비행 중의 HCUR 기체의 진동 응답 특성을 적절히 나타낼 수 있음을 확인할 수 있다. 더불어, 비행 속도에 따른 2P 진동수의 값[2,7]과 Table 2에 주어진 기체의 고유 진동수가 일치하지 않으므로 공진 회피가 가능함을 알 수 있다.
Table 2.
Natural frequencies of airframe stick model
2.3 HCUR 기체의 진동 응답 해석
70∼250 knots의 비행속도에서 CAMRAD II 해석으로부터 얻은 2P의 Lift-offset 로터 허브 진동 하중[2] 성분인 Fx2P, Fz2P, 및 My2P를 GVT 모델의 로터 허브 위치의 노드(node 24)에 가하고, 기체 주요 위치에서의 기체 축 (x-축) 방향 및 기체 수직 축 (z-축) 방향의 2P 진동 응답을 계산한다. 이 때, 3종류의 로터 허브 진동 하중을 모두 사용한 경우 (Fx2P+Fz2P+My2P), 2종류의 로터 허브 진동 하중을 이용한 경우 (Fx2P+Fz2P, Fx2P+My2P, 및 Fz2P+My2P), 각각의 로터 허브 진동 하중을 개별적으로 적용한 경우 (Fx2P, Fz2P, 및 My2P) 등의 다양한 조합으로 GVT 모델을 가진한 결과를 비교함으로써 로터 허브 진동 하중 성분들이 각각 미치는 영향을 규명한다. 원격 조종 장치(node 4), 동체-샤프 트(shaft)의 연결부(node 9), 날개의 뿌리(node 509), 및 끝단(node 35)의 총 4곳의 주요 위치에서 기체 축 및 수직 방향의 2P 기체 진동 응답을 계산한다.
3. 연구 결과
전술한 방법을 이용하여 다음의 Fig. 6에 70 knots의 비행 속도에서의 HCUR의 로터 허브 진동 하중과 기체 진동 응답 사이의 상관 관계를 조사하여 그래프로 나타내었다. 기체 주요 위치에서의 기체 축 방향(longitudinal direction)의 2P 진동 응답(Fig. 6(a))의 경우, 3종류의 2P 로터 허브 진동 하중이 동시에 작용할 때(Fx2P+Fz2P+My2P)의 진동 응답의 크기가 2P 로터 허브 피치 모멘트(My2P)만 작용할 때보다 작음을 확인할 수 있다. 즉, Fx2P 및 Fz2P에 의하여 My2P의 가진에 의한 2P 기체 진동 응답의 일부가 감소된다는 것을 알 수 있다. 각각의 허브 진동 하중을 개별적으로 적용했을 때(Fx2P, Fz2P, 및 My2P)의 진동 응답 중, My2P의 결과가 가장 크다. 2종류의 로터 허브 진동 하중을 함께 적용한 3개의 결과에서도 My2P가 포함된 2개의 진동 응답(Fx2P+My2P 및 Fz2P+My2P에 의한 가진)이 My2P가 포함되지 않은 Fx2P+Fz2P를 이용한 진동 응답 결과보다 더 크다. 이러한 결과들로부터 기체 축 방향으로의 진동 응답에 대하여 진동 하중 성분 중 My2P의 영향이 가장 지배적이라는 것을 보여준다. 또한, 모든 가진 조건의 진동 응답을 고려할 때, 원격 조종 장치에서의 진동이 가장 심한 것을 예측할 수 있다.
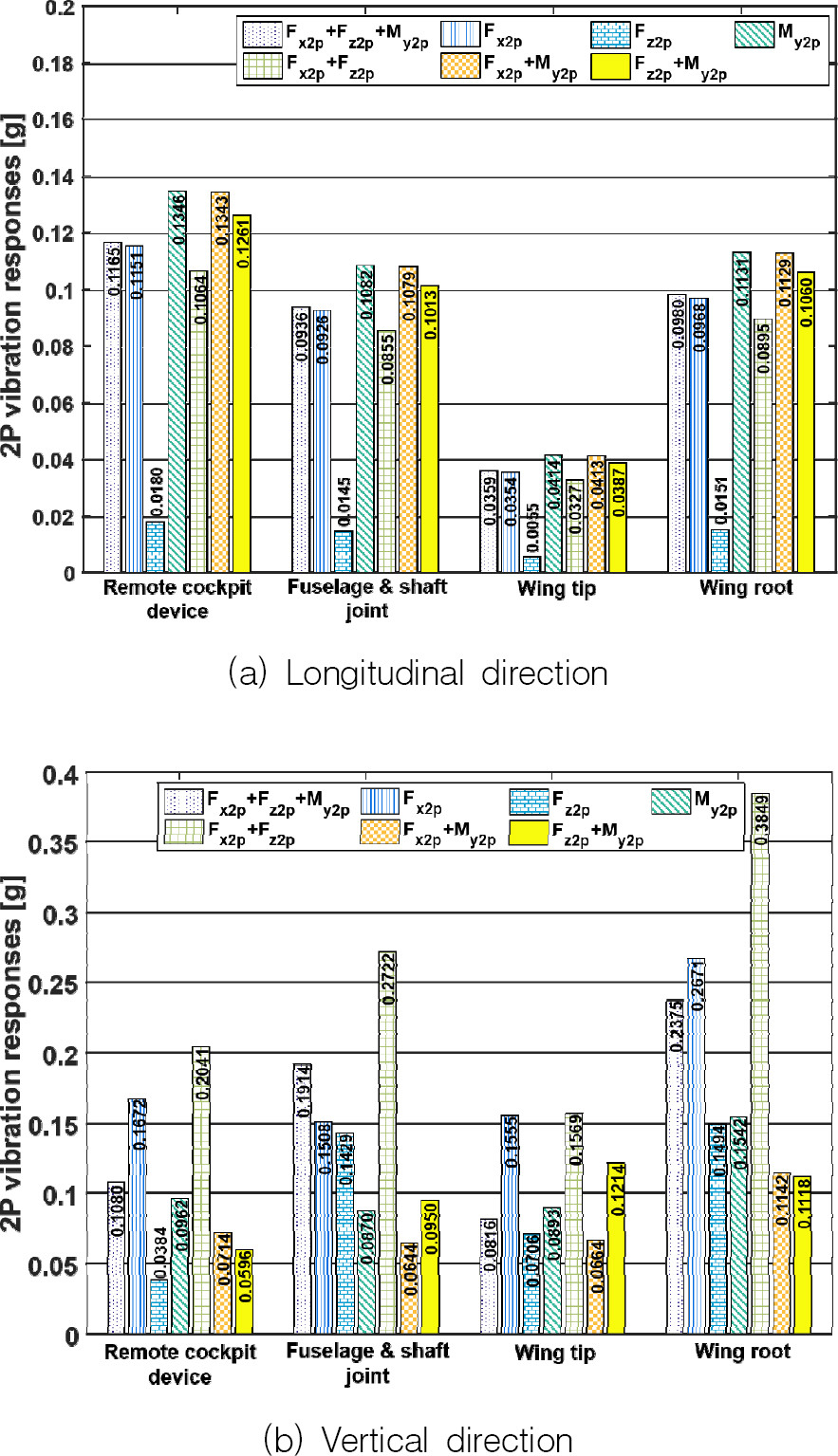
기체 수직 방향(vertical direction)으로의 2P 진동 응답(Fig. 6(b))의 경우, Fx2P에 의한 진동이 Fz2P에 의한 결과보다 크게 얻어졌다. 이는 로터 허브에 작용하는 Fx2P가 만들어내는 기체의 피치 운동으로부터의 수직 방향의 진동 응답이 Fz2p의 가진으로부터의 수직 방향의 진동 응답보다 크게 얻어졌기 때문으로 사료된다. 모든 위치에서의 수직 방향의 기체 진동 응답은 Fx2P 와 Fz2P가 함께 작용하였을 때, 가장 크게 얻어졌으며, My2P를 추가하여 3종류의 로터 허브 진동 하중이 동시에 기체를 가진할 때(Fx2P+Fz2P+My2P), Fx2P와 Fz2P가 함께 가진했을 때보다 진동 응답이 작으므로, My2P를 추가하여 기체 진동 응답의 크기가 감소됨을 알 수 있다. 3종류의 로터 허브 진동 하중이 함께 기체를 가진 할 시에 날개 뿌리(root)에서의 수직 방향 진동이 가장 크다는 것을 확인하였다.
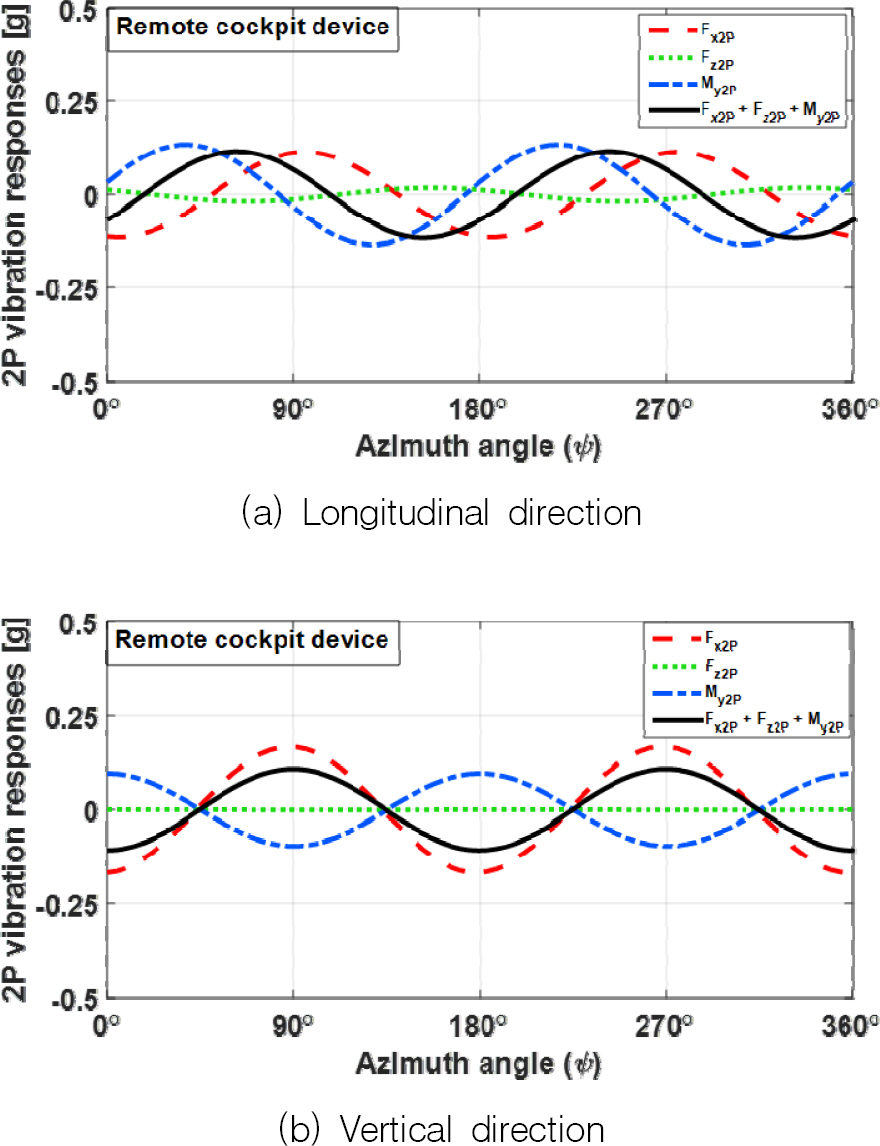
Fig. 7은 Fig. 6에 주어진 원격 조종 장치 위치에서의 2P 기체 진동 응답을 로터 한 바퀴 회전에 대하여 보여준다. Fig. 7(a)에서 보듯이 기체 축 방향의 진동의 경우, Fz2P에 의한 기체 진동 응답의 크기는 상당히 작으며 My2P에 의한 기체 진동 응답이 Fx2P에 의하여 13.4%만큼 감소되는데 이는 두 그래프 사이의 위상차에 기인함을 알 수 있다. 기체 수직 방향의 진동 응답의 경우(Fig. 7(b)), Fx2P에 의한 기체 진동 응답이 My2P 에 의하여 감소되며 이는 두 진동 응답의 위상이 반대이기 때문이다. Fig. 7에 얻어진 결과로부터 진동 응답의 진폭과 위상을 통하여 앞선 Fig. 6의 결과의 원인을 적절히 분석할 수 있다.
150 knots에서의 로터 허브 진동 하중과 기체 진동 응답 사이의 관계를 Fig. 8에 나타내었다. 기체 축 방향으로의 2P 진동 응답의 결과(Fig. 8(a))에서는 앞의 예제와 동일하게 3종류의 로터 허브 진동 하중 중 My2P의 영향이 가장 크다는 것을 확인할 수 있다. 두 종류의 로터 허브 진동 하중을 동시에 적용할 경우, My2P를 포함한 경우(Fx2P+My2P 및 Fz2P+My2P에 의한 가진)의 진동 응답이 Fx2P+Fz2P을 가진한 결과보다 크므로 기체 축 방향으로의 진동 응답에 대하여 My2P의 영향이 지배적임을 제시한다.
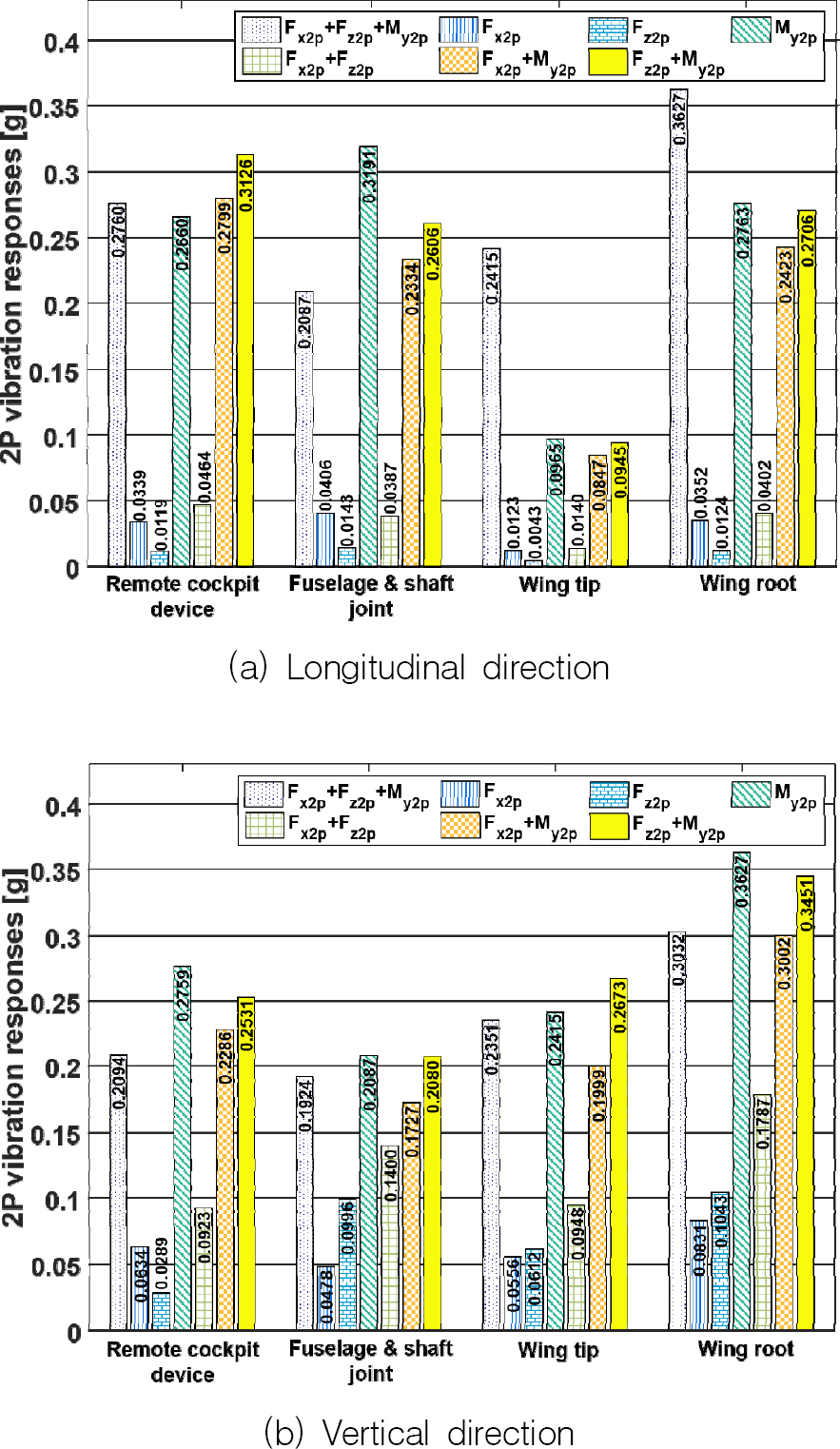
기체의 수직 방향으로의 2P 진동 응답의 경우(Fig. 8(b)), 3종류의 로터 허브 진동 하중 중 My2P에 의한 기체 진동 응답이 가장 크게 얻어졌으며 이는 Fig. 8(a)의 진동 응답의 결과와 동일하다. 즉, 70 knots의 Fig. 6의 결과와 비교 시, 비행 속도가 150 knots로 증가하면서 3종류의 로터 허브 진동 하중 중 My2P의 영향력이 기체 축 방향 및 수직 방향의 진동 응답에서 모두 증가하고 Fx2P의 영향력이 감소함을 알 수 있다. 3종류의 로터 허브 진동 하중이 동시에 기체를 가진 한 경우의 2P 기체 진동 응답이 My2P에 의한 단독 가진의 결과보다 최대 24.1 % 만큼 작게 얻어졌으며, 이는 기체 진동 응답에 대하여 Fx2P 및 Fz2P에 의하여 My2P의 영향력이 감소하였기 때문으로 판단된다.
로터 진동 지수(VI)가 최대의 값(Fig. 4)을 갖는 230 knots의 비행 속도에서의 결과를 Fig. 9에 정리하였다. 기체 축 방향으로의 2P 진동 응답과 로터 허브 진동 하중의 상관 관계(Fig. 9(a))의 결과는 전술한 Fig. 8(a)의 150 knots의 결과와 유사하게 얻어졌으며 3종류의 로터 허브 진동 하중 중 My2P가 가장 중요하게 작용 한다. 3종류의 로터 허브 진동 하중이 동시에 기체를 가진 할 경우, 원격 조종 장치의 위치에서 가장 큰 진동 응답을 보였다. 또한, 모든 조합의 가진 조건을 고려했을 때, 원격 조종 장치 위치에서 가장 심한 진동 응답이 관찰되었다.
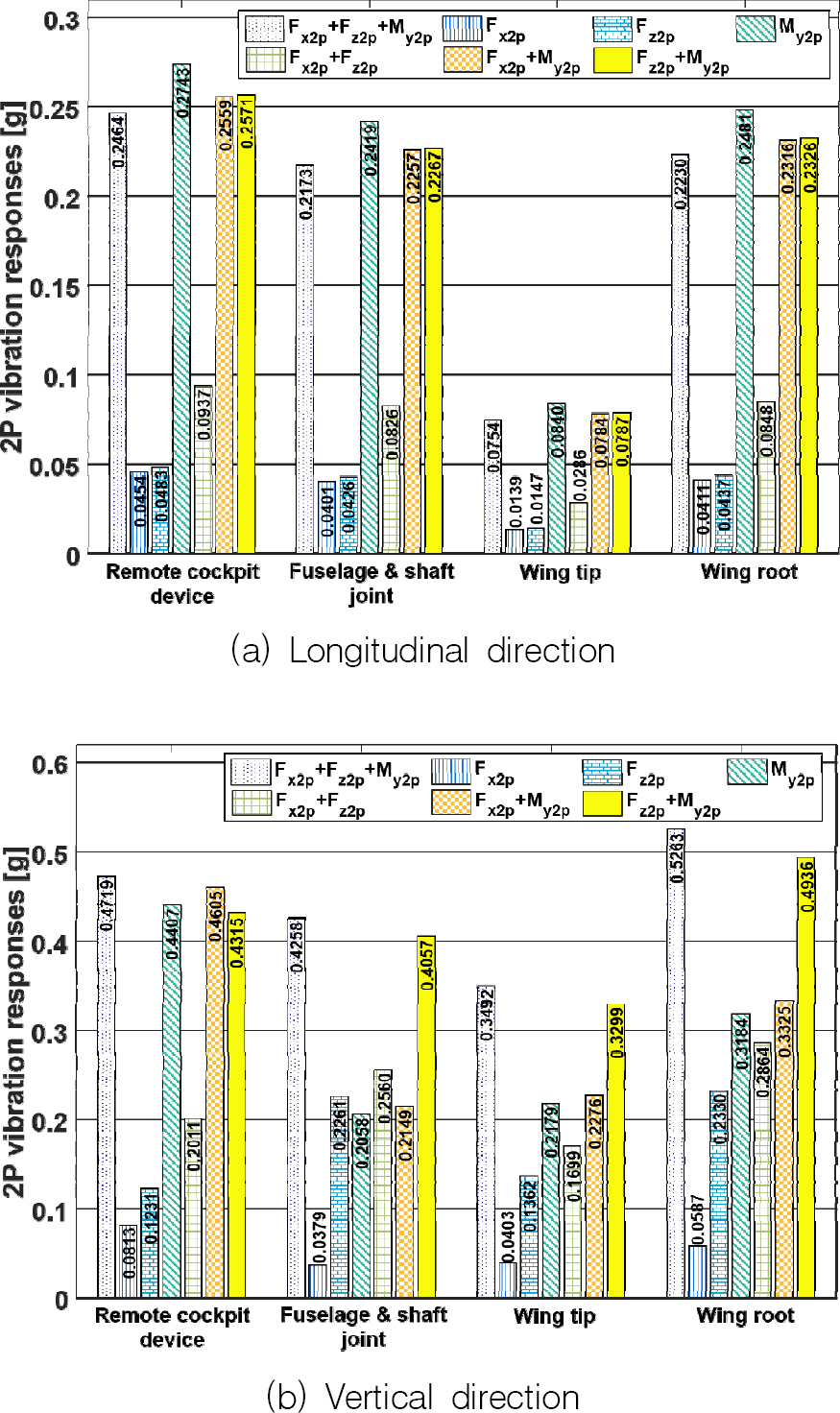
기체 수직 방향으로의 2P 진동 응답(Fig. 9(b))의 경우, 전술한 150 knots에 비하여 세가지 로터 허브 진동 하중 성분의 가진에 대한 진동 응답의 크기가 최대 125.4 % 만큼 증가하였으며, 앞서 살펴본 예제들과 유사하게 대부분의 기체 위치에서 My2P의 영향이 3종류의 로터 허브 진동 하중 성분들 중 가장 지배적임을 알 수 있다. 그러나 3종류의 로터 허브 진동 하 중이 동시에 기체를 가진 할 경우(Fx2P+Fz2P+My2P), My2P 만 기체에 작용할 경우보다 큰 진동 응답이 얻어졌으며, 이로부터 Fx2P 및 Fz2P가 수직 방향의 기체 진동 응답을 증가시킴을 확인할 수 있다. 70 및 150 knots의 결과와 흡사하게 3종류의 로터 허브 진동 하중이 동시에 기체를 가진 할 때, 기체의 주요 위치들 중 날개 뿌리에서의 기체 수직 방향의 진동 응답이 가장 크게 얻어졌다. 모든 조합의 가진 조건을 고려했을 때, 날개 뿌리의 위치에서 가장 강한 진동 응답 결과가 관측되었다.
Fig. 10은 Fig. 7과 마찬가지로 Fig. 9의 결과 중 원격 조종 장치 위치에서의 기체 진동 응답을 로터 한 바퀴 회전에 대하여 나타내었다. Fig. 9(a)에 주어진 기체 축 방향에 대한 결과에서는 Fx2P에 의한 기체 진동 응답과 Fz2p에 의한 결과가 진폭뿐만 아니라 위상에 있어서도 상당히 유사함을 알 수 있다. 더불어, My2P에 의한 기체 진동 응답이 Fx2P 및 Fz2P에 의하여 진폭이 10.2 % 만큼 감소되며 위상 또한 변화하는 것을 확인하였다. 이는 각 진동 응답의 위상차가 그 원인임을 확인할 수 있다. Fig. 9(b)는 기체 수직 방향에 대한 결과를 보여주며 각각의 진동 응답의 위상차를 고려 시, Fx2p 및 Fz2p에 의하여 My2P의 진동 응답의 진폭 크기가 7.1 % 만큼 증가됨을 알 수 있다.
Fig. 10.
2P airframe vibration responses at remote cockpit device for rotor one revolution (230 knots)
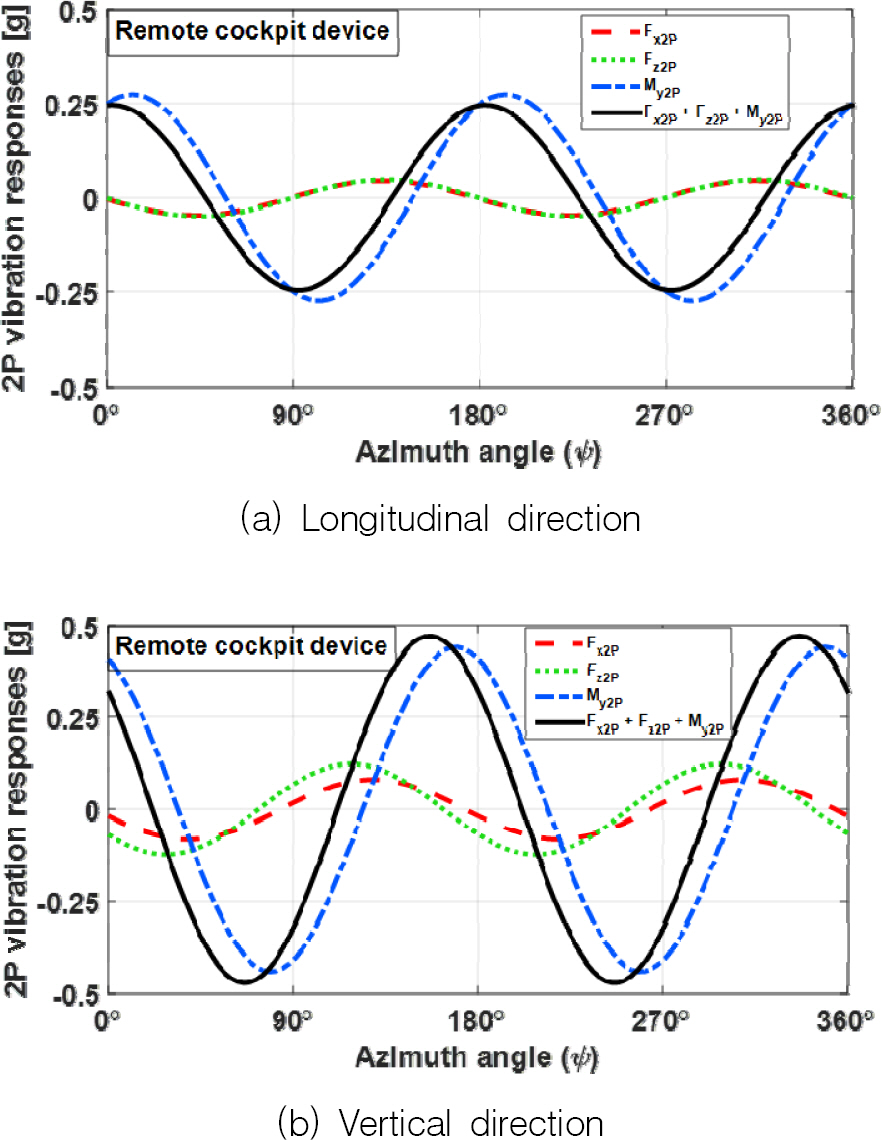
Fig. 11은 HCUR의 최대 비행속도인 250 knots에서의 로터 허브 진동 하중과 기체 진동 응답 사이의 상관 관계를 보여준다. 기체 축 방향의 진동 응답(Fig. 11(a))의 경우, 모든 위치에서 3종류의 로터 허브 진동 하중이 동시에 기체를 가진한 결과와 My2P만 기체에 작용한 결과가 상당히 유사하게 얻어졌다. 따라서 다른 두 종류의 로터 허브 진동 하중(Fx2P 및 Fz2P)은 기체 축 방향으로의 진동 응답에 대하여 미미한 역할을 하는 반면, 대신 My2P가 가장 큰 영향을 가하고 있음을 알 수 있다. 두 종류의 로터 허브 진동 하중을 함께 고려하였을 때, Fz2P와 My2P가 함께 기체를 가진 할 경우(Fz2P+My2P)의 결과가 모든 위치에서 가장 크게 얻어졌으며, 이로부터 Fz2P에 의하여 My2P에 의한 기체 진동 응답이 증가됨을 알 수 있다. 그에 반하여, Fx2P 와 My2P를 동시에 로터 허브에 작용할 시 (Fx2P+My2P), My2P만 기체를 가진 할 경우보다 작은 진동 응답을 보이므로 Fx2P는 My2P에 의한 기체 진동 응답을 일부 상쇄시킴을 확인할 수 있다.
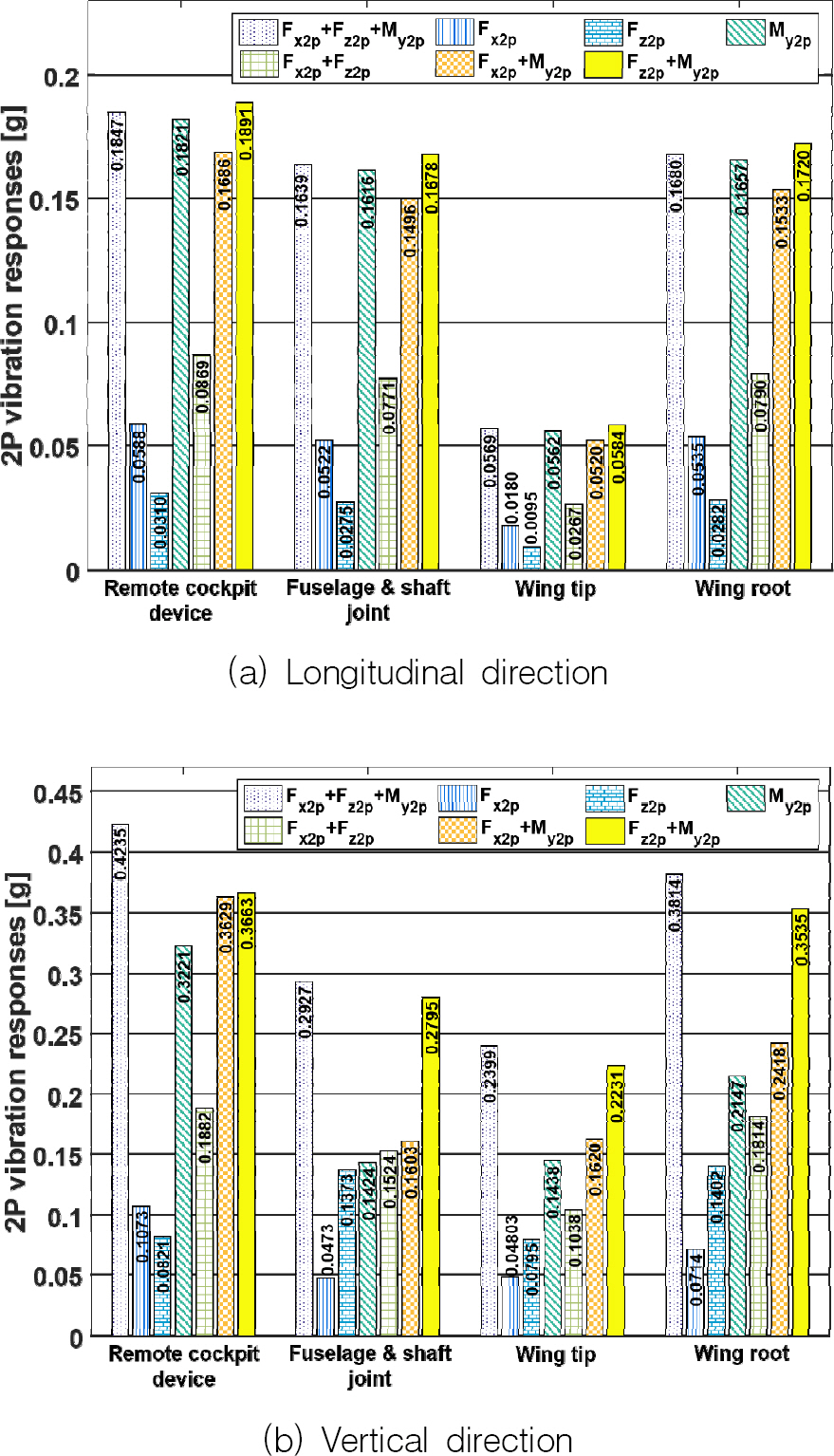
기체 수직 방향의 진동 응답(Fig. 11(b))은 전술한 230 knots의 결과에 비하여 다소 크기가 감소하였으나, 여전히 높은 수준의 진동 응답을 모든 기체 위치에서 나타내고 있다. 앞의 예제들과 마찬가지로 모든 위치에서 3종류의 로터 허브 진동 하중 중 My2P가 기체 진동 응답에 대한 가장 주요한 영향력을 가지고 있다. 또한, 3종류의 로터 허브 진동 하중이 동시에 기체를 가진 할 시, 가장 큰 기체 진동 응답이 관찰된다. 이와 같은 결과들로부터 Fx2P와 Fz2P가 My2P에 의한 기체 진동 응답을 증가시킨다는 결론을 얻을 수 있다.
앞에서 살펴본 결과들로부터 HCUR Lift-offset 로터의 3종류의 2P 허브 진동 하중 중, My2P가 기체의 주요 위치에서 기체 축 방향 및 수직 방향으로의 2P 진동 응답에 가장 지배적인 성분임을 판단할 수 있다. 단, 비행 속도 및 진동 응답 방향에 따라 2P 허브 진동 하중의 조합의 기체 진동 응답에 대한 효과는 다르게 얻어지기도 하였으며 이는 각각의 로터 허브 진동 하중 성분에 대한 기체 진동 응답의 위상차에 기인함을 확인하였다.
4. 결 론
본 연구에서는 Lift-offset 동축반전 로터, 날개, 및 프로펠러를 함께 사용하는 5,000 lb급의 고속 비행 복합형 무인 회전익기에 대하여 로터 허브 진동 하중과 기체 진동 응답 사이의 상관 관계를 조사하였다. 회전익기 통합 해석 코드인 CAMRAD II를 이용한 선행 연구 결과로부터 얻어진 2P 로터 허브 진동 하중을 상용 유한요소 해석 프로그램인 MSC.NASTRAN을 이용한 본 연구의 1차원 기체 구조 모델(1D stick 모델)에 적용하여 2P 기체 진동 응답 해석을 수행하였다. 저속 비행을 제외한 대부분의 비행 속도 영역에서 로터 허브 피치 모멘트의 2P 진동 하중 성분(My2P)이 기체 축 방향과 기체 수직 방향의 2P 진동 응답 모두에 대하여 모두 지배적인 영향을 보였다. 본 논문의 고속 비행 복합형 무인 회전익기의 기체 진동 응답 수준이 매우 높게 얻어졌으며, 이는 Lift-offset 동축반전 로터를 사용하는 복합형 헬리콥터의 단점이므로 이를 적절히 감소시킬 수 있는 능동 진동 제어 기법 등의 적용이 필요함을 확인하였다.
PDF Links
PubReader
ePub Link
Full text via DOI
Download Citation
