고속 상륙돌격장갑차의 저항 및 추진 성능에 관한 수치 분석
Numerical Analysis on the Resistance and Propulsion Performances of High-Speed Amphibious Assault Vehicles
Article information
Abstract
The hydrodynamic characteristics of amphibious assault vehicles are investigated using commercial CFD code, STAR-CCM+. Resistance performances of a displacement-type vehicle and a semi-planing type vehicle are analyzed in calm water. The self-propelled model is also computed for the semi-planing type vehicle. All computations are performed using an overset mesh system and a RANS based flow-solver coupled with a two-degree of freedom equations of motion. A moving reference frame is applied to simulate revolutions of impeller blades for a waterjet propulsion system. Grid dependency tests are performed to evaluate discretization errors for the mesh systems. The numerical analysis results are compared with the experimental results obtained from model tests. It is shown that RANS is capable of investigating the resistance and self-propulsion characteristics of high-speed amphibious assault vehicles. It is also found that a fully covered side skirt, which is covering tracks, reduces resistance and stern trim, besides increasing propulsive efficiency.
1. 서 론
상륙돌격장갑차는 상륙작전 시 해병대의 핵심 전력으로 상륙함에서 진수 후 수상 운행장치를 전개하여 체계 형상을 변환하고, 별도의 수상 추진장치인 워터제트 추진시스템(waterjet propulsion system)으로 추력을 발생시켜 고속 해상 기동을 실시한다. 상륙 준비 단계에서는 육상 장갑차의 형태로 체계 형상을 환원하며 수납식 궤도(retractable track)를 내려 상륙과 동시에 육상 기동 및 전투 임무를 수행한다.
해상에서 고속 기동 중인 상륙돌격장갑차는 수력학 적(hydrodynamic) 관점에서 선박의 일종으로 간주할 수 있다. 상륙돌격장갑차는 설계 속력과 항주 자세 등에 따라 배수량형(displacement), 반활주형(semi-planing) 및 활주형(planing) 선박 형태로 분류할 수 있다. 일반적으로 상선은 선박의 무게가 수면 하부의 잠긴 부피에 해당하는 부력과 평형을 이루는 배수량형 선박으로 분류된다. 반활주형과 활주형 선체를 갖는 고속 상륙돌격장갑차는 Fig. 1과 같이 해상 속력이 증가하여 Froude수가 커지면 차체의 침수 면적에 작용하는 양력이 증가하므로 종경사각(trim angle)과 부상량(heave or rise)이 해상속력의 함수로 변화한다. 즉, 양력의 증가로 차체가 수면 위로 부상하고 부력이 감소하므로 장갑차의 무게와 평형을 이루는 힘 중 양력과 부력의 비율이 달라지기 때문이다. 결국 장갑차의 종경사각과 부상량은 장갑차에 작용하는 힘과 모멘트의 평형에 의해 결정되며 작용하는 힘의 성분은 상기에서 언급한 동적 특성을 갖는 양력, 정적 특성을 갖는 부력, 중력, 저항 및 추력이다.
선박이 전진하면서 받는 압력을 선박의 침수 표면적에 대해 적분하여 얻은 힘은 조파(wave-making) 저항이며 그 크기는 선박이 만들어내는 파도의 형상과 크기에 따라 결정된다. 배수량형 선박은 동일 길이에서 속력이 빠를수록, 즉 Froude수가 클수록 전체 저항에서 조파 저항이 차지하는 비율이 높아진다. Froude 수의 정의는 식 (1)과 같으며, VS는 선속, g는 중력가속도, LS은 선박의 길이이다.
조파 저항이 증가하면 높은 추력을 발생시키기 위해 필요한 엔진 출력도 증가하므로 설계 Froude수 범위에 대한 정확한 분석이 필요하다. 상선의 경우, 통상 저속 비대선인 300,000톤급 원유운반선의 Froude수는 0.14 수준이며 35,000톤급 정유운반선의 경우 0.19 수준이다. 상선 중 속력이 빠른 9,000 TEU(Twenty-foot Equivalent Unit)급 컨테이너선의 경우에도 0.23 정도로 최대 0.3을 넘지 않는다. 자동차 운반선이나 고속선인 구축함의 Froude수는 각각 0.24, 0.28 수준으로 설계된다[2]. 반면, 차기 상륙돌격장갑차는 고속 해상 기동 시 Froude수가 0.55∼0.68의 범위를 상회할 것으로 추정되므로[3], 조파 저항을 줄이기 위해 상선과 차별되는 선체 형태가 필요하다.
상륙돌격장갑차를 대상으로 수행한 저항 및 자항 성능 연구는 무기체계 개발사업의 특성 상 공개된 자료가 많지 않다. 모형시험 분야에서 Brown 등[4]은 궤도형 상륙돌격장갑차의 정수 중 모형시험을 통하여 궤도 측면과 하부 덮개 및 수납식 궤도 적용 시 저항 의 변화를 평가하였다. Helvacioglu 등[5]은 차륜형 수륙양용차의 선수판(bow vane) 설치에 따른 도하 시 저항을 모형시험을 통해 분석하였다.
수치해석 분야에서 Jang 등[6]은 궤도형 상륙돌격장갑차의 선미익 설치 받음각에 따른 저항을 분석하였으며, Jang 등[7]은 차륜형 상륙돌격장갑차의 선수판 설치 여부에 따른 저항과 항주자세 등 수동역학적 성능을 분석하였다. Kim 등[8]은 워터제트 추진 궤도형 상륙돌격장갑차의 실차 크기 자항 성능을 전산유체역학 기반 수치 기법으로 추정하는 연구를 수행하였다.
무기체계 개발과정에서 차기 상륙돌격장갑차의 육·해상 기동을 모두 고려하여 기본 선형을 배수량형, 반활주형 및 활주형 중 어떠한 형태로 선정할 것인가에 대한 설계와 저항·자항 성능에 대한 정확도 높은 초기 분석이 중요하다. 하지만 탐색개발사업 단계에서 개발 기관의 정확한 방향 설정을 위해서는 상기의 선행 연구결과만을 토대로 분석하기에는 한계가 있다. 따라서 본 연구에서는 고속 상륙돌격장갑차의 저항 및 자항 추진 성능 분석을 위해 자유 수면의 효과와 유체-물체 간 동적 상관관계 기반의 운동해석을 포함한 장갑차 주위 난류유동 해석을 수행하였다. 수치 해석 시 상용 CFD(Computational Fluid Dynamics) 코드인 STAR-CCM+ 버전 14.02을 활용하였다. 제 2장에서는 수치기법 및 검증 방법에 대해 기술하였다. 제 3장에서는 조파이론에 근거하여 배수량형 및 반활주형 상 륙돌격장갑차의 험프 속력(hump speed)을 산출하고, 수력학적 성능을 해석하여 험프 구간을 포함한 저항 곡선을 분석하였다. 제 4장에서는 반활주형 상륙돌격장갑차의 자항 성능을 평가하고 모형시험을 통해 검증한 내용을 기술하였다. 검증된 수치해석 기법을 이용하여 궤도에 의한 난류와 에너지 소산을 방지하기 위해 장갑차 측면에 적용한 궤도 측면 덮개(side skirt)의 형상이 자항 성능 및 항주 자세에 미치는 영향을 평가하였다.
2. 수치기법 및 검증 방법
2.1 지배방정식 및 난류모델링
자유 수면과 함께 장갑차 주위 점성유동 해석을 위하여 공기와 물을 모두 포함하는 비압축성 난류 유동에 대한 지배방정식은 연속방정식인 RANS(Reynolds averaged Navier-Stokes) 방정식을 사용하였으며, 적분형태는 다음과 같다.
위 식에서 t는 시간, ρ는 유체의 밀도, V는 제어체적을 의미하며, 벡터 V는 유체의 속도를 의미한다. dS 는 제어체적 표면의 미소 면적 벡터를 나타낸다. 운동량 방정식에서 p는 압력, f는 체적력 벡터를 의미한다. Fviscous는 제어체적 표면에 작용하는 점성력 벡터이다.
상기 서술한 지배방정식을 풀기 위하여 유한체적법(finite volume method)의 수치기법을 사용하였다. 시간차분화는 2차 정도의 암시적(implicit) Euler 도식법(scheme)을 이용하여 수행하였으며, 지배방정식의 공간항인 대류항과 확산항은 해석 비용 절감을 위하여 상류 도식법(upwind scheme)을 이용하여 이산화하였다. 속도-압력 간 연성해석은 속도와 압력을 별도로 반복 계산하는 분리(segregated) 유동 접근법을 사용하였으며, SIMPLE(Semi-Implicit Method for Pressure Linked Equation) 알고리즘[9]을 기반으로 하였다.
RANS 방정식에서 시간 평균된 난류의 성분을 수치적으로 생성하기 위하여 난류 모델링을 사용하였다. 상륙돌격장갑차는 각진 형상으로 인해 선미부의 박리 유동에 의한 형상 저항이 크기 때문에, 와류(vortex flow) 해석에 적합한 k-ω SST(Shear Stress Transport) 난류모델[10]을 사용하였고, 장갑차 표면의 경계층 구현은 All y+ 벽함수(wall function) 기법[11]을 사용하였다.
2.2 자유 수면 모델링
상륙돌격장갑차는 해상 기동 시 종경사각이나 부상량 등 거동의 변화가 대형 선박 대비 크기 때문에, 자유 수면의 변화가 장갑차에 미치는 영향을 평가하기 위하여 자유 수면에 대한 모델링을 포함하여 해석을 수행하였다. 자유 수면에 대한 모델링은 VOF(Volume Of Fraction) 기법[12]을 사용하였다. 평면파(flat wave) 조건에 대해 조류 속도와 풍속은 장갑차의 전진 속력과 동일하게 입력하였으며, 정수 중 해수면의 높이, 수직 방향, 해수와 공기의 밀도 등을 Table 1과 같이 입력하였다.
2.3 장갑차 운동 해석 기법
상륙돌격장갑차는 해상 속력, 워터제트 추진 시스템의 성능 및 수상 운행 장치의 최적화에 따라 항주 자세가 달라진다. 해상 기동 시 조종수의 시야 확보 및 탑재된 포의 사격 각도 등을 고려할 때 장갑차의 운동해석은 필수적이다.
본 연구에서는 중첩 격자 기법(overset mesh method)을 이용하여 전체 유동장을 해상 환경 혹은 모형 수조 등 배경 격자 영역과 장갑차 주위 근접장을 포함하는 중첩 격자 영역으로 구분하였다. 상륙돌격장갑차가 높은 Froude수 범위에서 해상 기동을 하며 파랑 등 외부 교란에 취약하고 정수 중에서도 자세 변화가 크기 때문에 중첩격자 기반 동적 유체-물체 상호작용(overset mesh based dynamic fluid body interaction) 해석법을 적용하여 장갑차의 운동을 모사하였다. 중첩 격자 체계는 장갑차의 중량과 무게 중심에 대하여 유체에 의해 가해지는 힘과 모멘트에 따라 장갑차와 함께 이동한다. 상륙돌격장갑차의 운동 해석을 위해 이용한 운동 방정식은 다음과 같다.
위 식에서 m은 장갑차의 질량이며, V는 장갑차의 운동 속도이다. F는 장갑차에 가해지는 힘으로 압력 저항, 마찰 저항, 중력, 추력 및 기타 외부 힘의 합력이다. ω는 장갑차의 회전 각속도이며, I는 관성 모멘트(moment of inertia)를 의미하며 M은 장갑차에 작용하는 모멘트의 합이다.
초기 조건으로부터 유체 흐름의 변화에 따라 상륙돌격장갑차에 작용하는 힘과 모멘트에 의해 그 자세가 변화한다. 본 연구에서는 유체력과 장갑차의 무게 및 관성 모멘트를 이용하여 6자유도 운동 중 종경사각과 부상량에 대해 계산을 수행하여 장갑차의 자세 변화를 추정하였다. 장갑차의 무게는 해석 영역에서 장갑차의 절반 만을 포함하고 있기 때문에 총 질량의 절반을 적용하였다. 장갑차의 배수량 및 관성 모멘트에 대한 해석 입력값은 무기체계 개발의 특성 상 공개가 어려우며 관성 모멘트의 경우 초기 형상에 대해 컴퓨터 보조 설계(CAD, Computer-Aided Design) 상용 프로그램의 관성 모멘트 산출 기능을 활용하여 획득하였다.
2.4 워터제트 추진 시스템의 임펠러 회전 구현
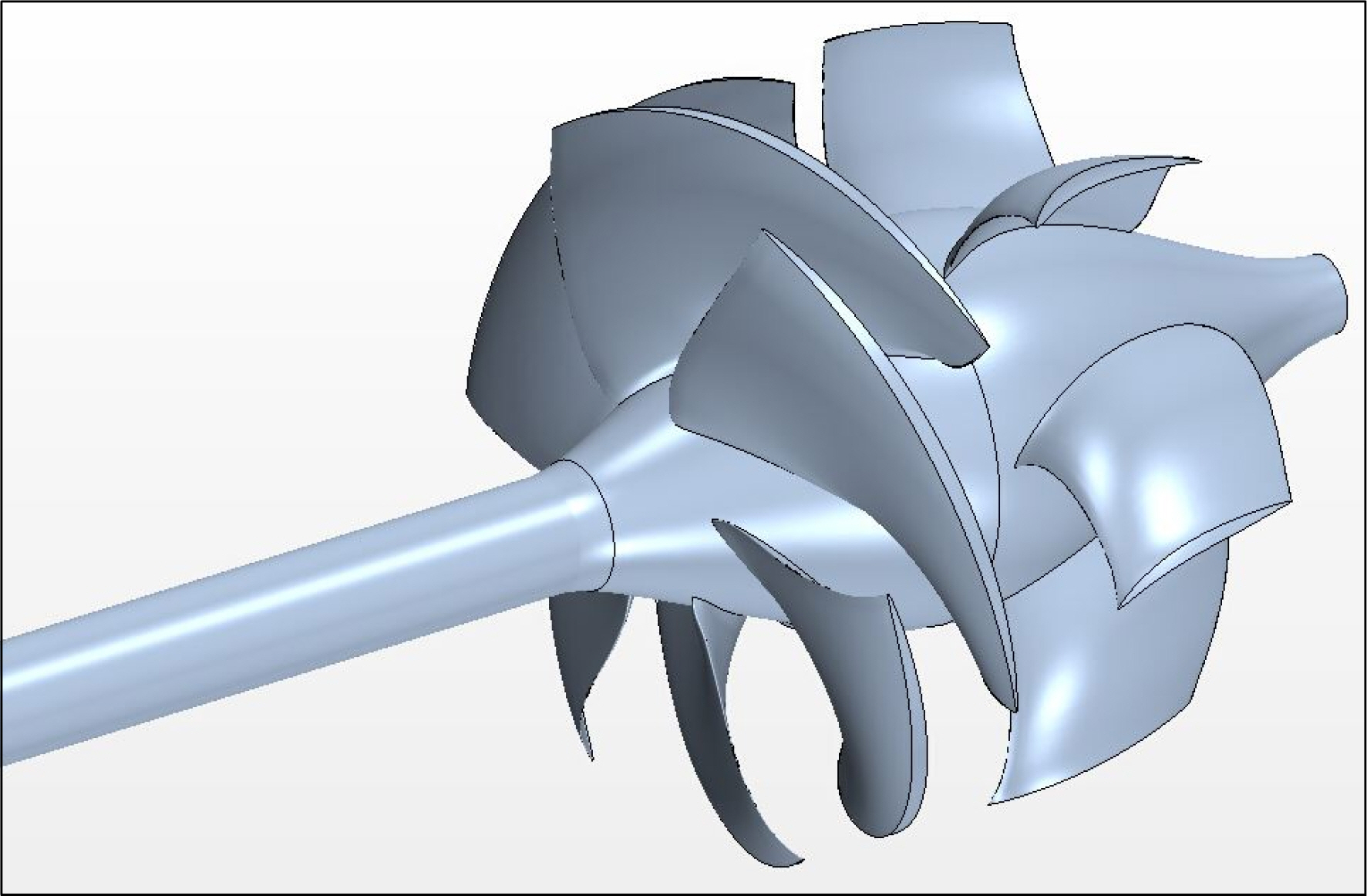
임펠러(impeller)의 날개 및 허브를 포함하는 회전 영역의 구현을 위하여 회전 좌표계에 따라 유체의 흐름을 해석하는 이동 좌표계(moving reference frame) 기법을 적용하였다. 본 기법은 격자가 실제로 움직이는 슬라이딩 격자(sliding mesh) 기법 대비 계산 비용의 절감 효과가 있다. 임펠러 회전 시 시계열 상 평균된 개념의 유체 거동을 모사하여 임펠러의 추력(thrust) 계수, 토오크(torque) 계수 및 유량 계수를 해석하였다. 저항 및 추진 성능 해석 시 캐비테이션(cavitation)이 발생하지 않는 비공동 상태로 가정하고 분석을 수행하였다. 워터제트 추진 시스템의 주요 정보를 Table 2에 기재하였으며, 그 형상을 Fig. 2에 도시하였다.
2.5 수치 분석 대상 및 검증 방법
상륙돌격장갑차의 저항 분석을 위한 대상 모델은 국방과학연구소 주관 상륙돌격장갑차-Ⅱ 탐색 개발 사업의 기본 설계 결과물 중 일부를 활용하였다. 추진 성능 분석을 위한 모델은 국방과학연구소에서 수행한 상륙돌격장갑차-Ⅱ 선행 핵심기술 연구의 결과물 중 일부를 활용하였다. 수상운행장치를 제외한 장갑차 차체의 형상과 주요 치수를 Table 3에 기재하였다. 수치 분석 결과의 검증을 위한 자료는 국방과학연구소에서 의뢰하여 2018년부터 2020년까지 서울대학교 선형공 학수조에서 실시한 모형시험 결과를 활용하였다. 모형시험 모델은 축척비 1:4.5로 기하학적 상사를 만족하여 제작되었으며, 궤도의 요철은 구현하지 않았다.
2.6 수치 격자 체계 및 경계 조건
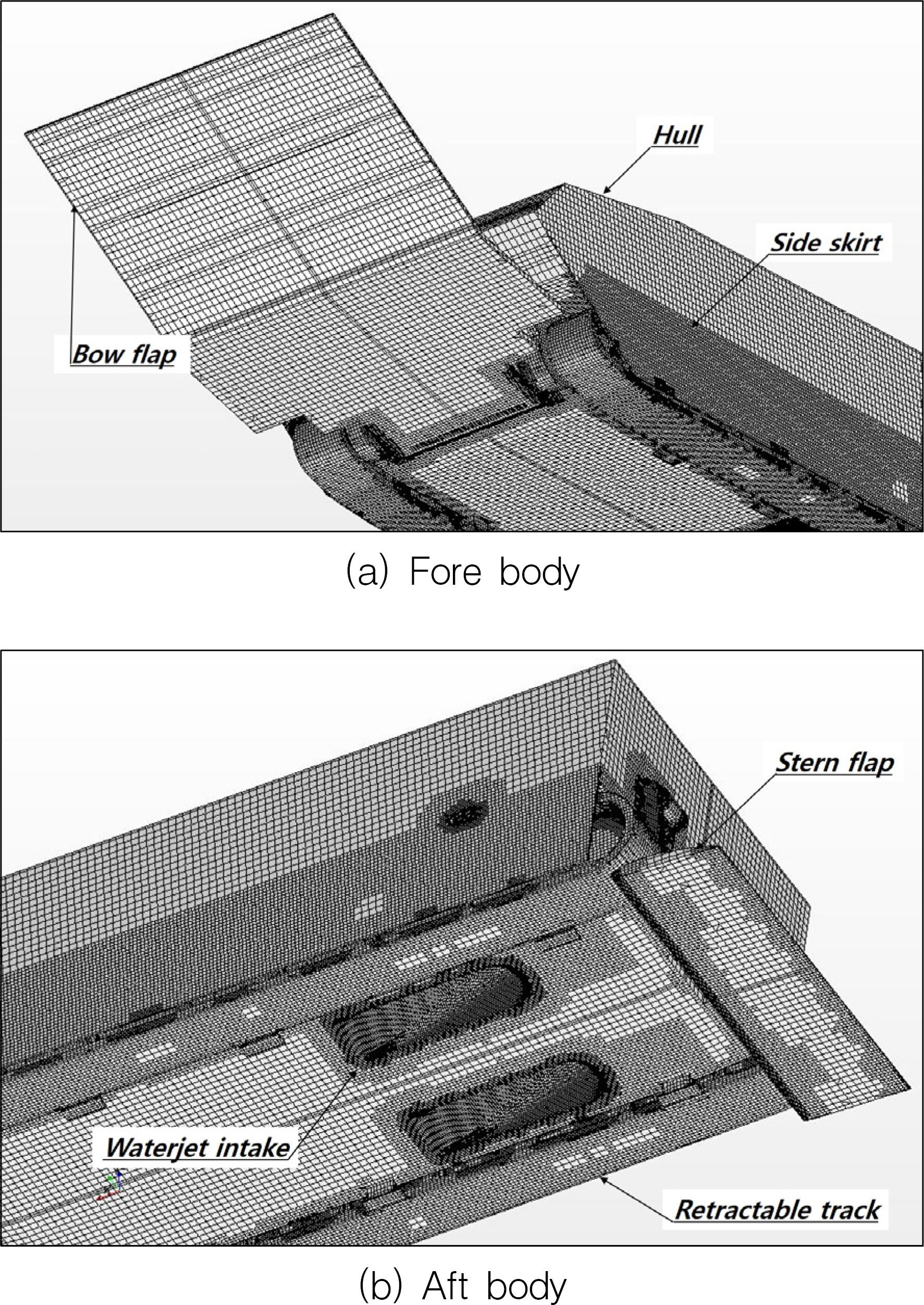
상륙돌격장갑차의 선수익, 선미익 및 측면익과 워터제트 추진 시스템, 궤도 등 복잡한 형상에 대해 모사가 가능하도록 표면 격자 체계를 구성하였다. Fig. 3은 반활주형 장갑차의 선수 및 선미부 표면 격자 체계이다.
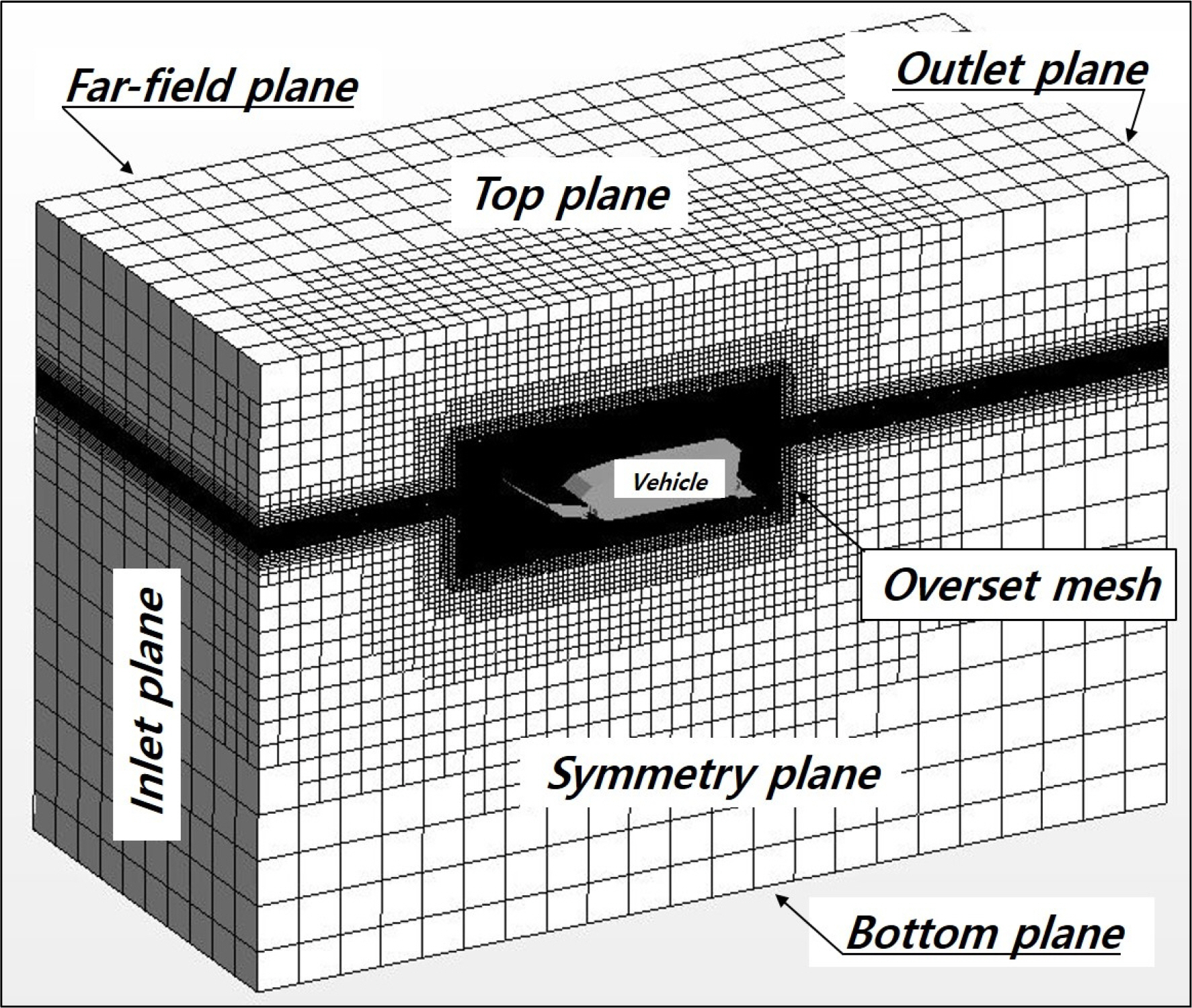
저항 해석을 위한 공간 격자 체계는 Fig. 4와 같다. 해석의 효율화를 위하여 장갑차의 우현부만 해석하였으며, 배경 격자와 중첩 격자에 대해 모두 다면체(polyhedral) 격자가 아닌 육면체(hexahedral) 격자 체계를 적용하여 격자 품질을 향상시키고 격자 생성 시간을 최소화하였다.
자유 수면의 변화가 장갑차의 종경사각 및 부상량에 미치는 영향을 해석하기 위하여 수면부의 격자 품질을 제어하였다. 자유 수면의 공간 격자를 성긴(coarse) 격자부터 조밀한(fine) 격자까지 다수의 계층을 통해 격자 체계를 세분화하였다. 성긴 격자는 장갑차의 세로 방향, 가로 방향, 수직 방향에 대하여 격자 기본 길이(base size)의 100 %, 400 % 및 50 %를 부여하였다. 조밀한 격자의 경우 횡 방향의 격자 분포는 고정하고 장갑차의 세로 방향과 수직 방향의 격자 크기를 기본 길이의 25 %, 6.25 %로 조정하였다. 중간 계층의 경우 격자 크기가 단계적으로 변화되도록 두 수치 사이의 값을 부여하였다.
경계 조건으로 배경 격자와 중첩 격자 간 중첩 격자 경계면을 부여하였다. 입구 경계면(inlet plane), 출구 경계면(outlet plane), 원방 경계면(far-field plane) 및 상·하부 경계면(top and bottom planes)에는 입구 속도 (inlet velocity) 조건을 부여하였다. 대칭면에는 대칭 경계조건을 두었으며, 장갑차 표면은 점성 해석을 위한 점착 벽면(no-slip wall) 조건을 지정하였다.
추진 성능 해석을 위한 격자는 워터제트 추진 시스템의 노즐 출구 후방의 유동 특성을 정밀하게 모사하기 위하여 저항 해석용 격자 체계를 수정하여 노즐 출구부와 그 후류 영역의 격자 조밀도를 증가시켰다. 자항 해석을 위한 표면 격자 체계를 Fig. 5에 도시하였으며, 워터제트 추진 시스템의 표면 격자 체계를 확대하여 Fig. 6에 나타내었다. 워터제트 추진 시스템의 성능해석을 위하여 임펠러와 허브가 포함되는 영역을 중첩 격자 영역 내에서 별도로 구분하였다.
이동 기준 좌표계 기법을 이용하여 임펠러의 회전 효과를 부여하였고 회전 영역은 Fig. 7에서 도시한 날 개의 앞전과 뒷전 등 정밀한 형상 모사를 위하여 다면체(polyhedral) 격자 체계를 사용하였다. 장갑차 주변의 중첩 격자와 배경 격자는 트리머(trimmer) 격자 생성법으로 격자를 구성하여 격자 생성 시간 및 해석 비용을 절감하였다.
3. 저항 분석 결과
3.1 조파이론 기반 선체 속력 및 험프 속력 분석
조파는 생성 원리 및 파의 진행 방향에 따라 확산파(diverging wave)와 횡파(transverse wave)로 구분되며, 횡파는 선박이 항해하면서 파를 생성하기 때문에 파의 진행 축은 선박의 진행 방향과 동일하고 파속(wave speed)은 선속과 유사한 값을 갖는다[13].
식 (7)에서 LW는 횡파의 파장, VS는 선속, g는 중력가속도를 나타낸다.
저속 기동 시에는 선박의 길이 LS 대비 횡파의 파장이 짧아 조파 저항이 작다. 선속 증가에 따라 횡파의 파장이 길어지게 되면, LW=LS의 관계가 성립하는 순간에 도달한다. 이때의 선속이 배수량형 선박의 선체 속력(hull speed)이며, 주어진 선박의 길이에 대하여 조파 저항 증가 경향을 기준으로 평가할 때 효율적인 선속 설계점(design point)의 마지노선이다.
선속이 증가하여 선수(bow)에서 생성되는 선수 횡파와 선미(stern)에서 생성되는 선미 횡파의 파골(wave trough)이 서로 일치하는 경우에 조파 저항이 급격히 커지게 된다.
선수파와 선미파의 파정(wave crest) 간 거리는 약 0.9LS이므로 식 (5)의 관계가 성립하는 경우에 저항이 크게 증가하는 험프 특성이 저항 곡선에서 나타난다.
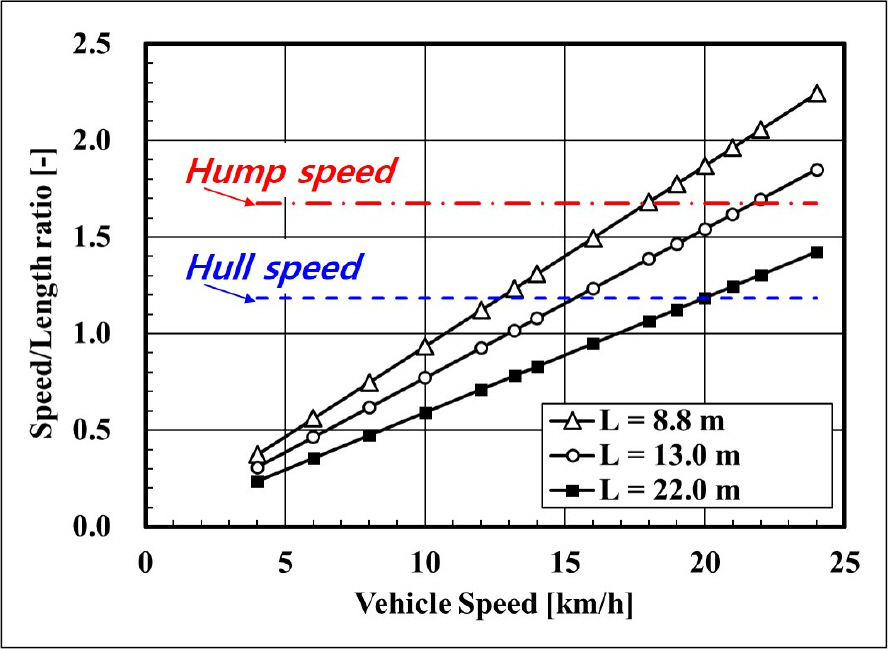
Fig. 8은 대표적인 배수량형[14] 상륙돌격장갑차인 미 해병대의 AAV7A1(Amphibious Assault Vehicle 7A1)의 속력-길이 비(speed-to-length ratio,
AAV7A1과 EFV(Expeditionary Fighting Vehicle)의 최종시험모델에 대해 상륙군이 해상 기동 후 전투수행능력의 변화를 분석한 연구[16]에서, 1시간 기동 후 탑승 상륙군의 24.4 %가 멀미(motion sickness)에 대한 인지 반응을 나타내었으며 2시간 경과 후 약 39.3 %가 멀미로 인한 심한 고통을 호소하였다. 또한 장갑차 탑승 전과 비교하여 전투 이동 능력, 사격 능력 및 통신 반응이 달라진 것으로 나타났다. 따라서 차기 상륙돌격장갑차의 설계 속력-길이 비를 결정할 때는 상륙 작전 거리, 장갑차의 차체 길이 뿐만 아니라 상륙을 위하여 상륙함에서 진수하여 목표 해안까지 도달하는 시간도 중요한 고려사항이다.
Fig. 8과 같이 차기 상륙돌격장갑차가 AAV7A1의 선형과 유사한 배수량형 선체를 도입할 경우 고출력 엔진을 탑재하여도, 선체 속력인 속력-길이 비가 약 1.19에 해당하는 해상 속력을 초과하는 경우에서는 추 진 효율이 저하될 것으로 예상한다. 또한 속력-길이 비가 약 1.68에 도달하여 험프 속력이 되면 선수 횡파와 선미 횡파의 파골이 일치하여 조파 저항이 증가하므로 요구 동력이 증가할 것으로 추정한다. 따라서 한정된 엔진 출력으로 목표 해상 속력을 달성하기 위해서는 배수량형 선체가 아닌 선체 속력 이후에 종경사각이 감소하고 부상량이 증가하여 수상 저항을 저감할 수 있는 반활주형 또는 활주형 선체가 요구된다.
3.2 격자 체계 의존성 분석
수치기법을 이용한 저항 해석을 위하여 정수 중 격자 체계 의존성을 분석하였다. 해석 대상은 반활주형 상륙돌격장갑차이며 정수 중 저항 해석은 실차 크기로 해석하였다. 격자 해상도는 중첩 격자 체계의 기본 크기와 자유 수면 구현을 위한 격자 조밀도를 변경하여 조절하였다. 조밀도에 따라 성긴 격자는 약 4.45×106개, 중간 격자는 약 6.67×106개, 조밀한 격자는 약 9.01×106개, 가장 조밀한 격자는 약 1.66×107개의 제어 체적으로 구성하였다.
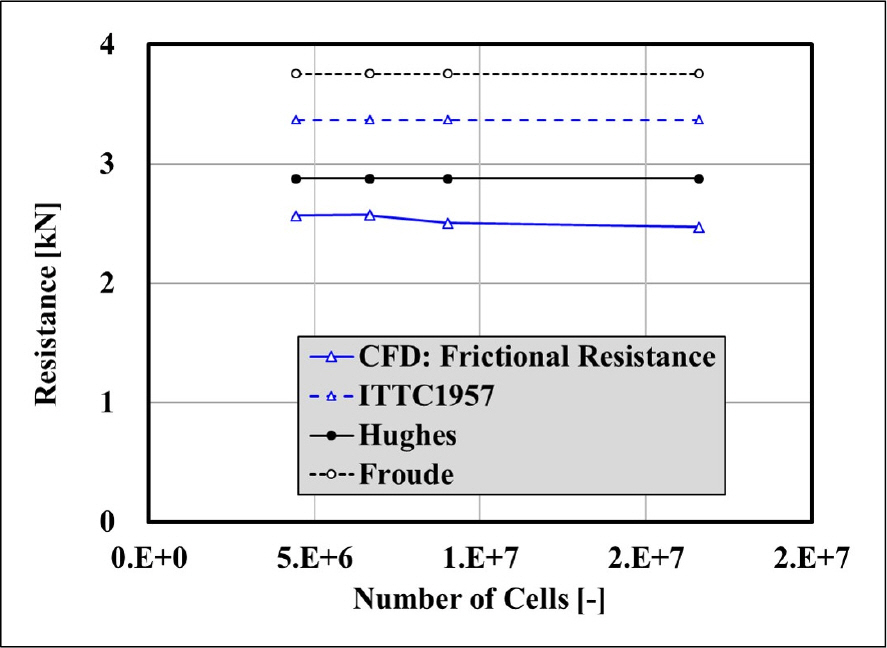
전 저항 및 마찰저항에 대한 격자 의존도 분석 결과를 Fig. 9에 나타내었다. 모형시험 결과는 Froude의 실선 저항추정법을 근간으로 한 2차원 외삽법[17]을 기반으로 실차 크기로 확장한 결과이다. 마찰저항은 별도 계측이 불가능하므로 ITTC(International Towing Tank Committee) 1957 모형선-실선 저항추정법[18]의 마찰저항 공식을 활용하여 도시하였다.
상륙돌격장갑차의 경우 선박 대비 전 저항 중 마찰저항의 크기가 작아 압력저항의 기여도가 큰 것으로 나타났다. 격자 조밀도에 따른 전 저항의 변화는 압력 저항의 수렴성과 관련이 있는 것으로 판단되며, 조밀도가 높은 격자에서 압력 저항을 포함한 전체 저항이 수렴되는 특성으로 볼 때 그 원인은 수치적 소산에 기인한 것으로 분석된다. 압력 저항의 수렴 특성을 나타내는 조밀한 격자에서 수치 계산 결과의 전 저항과 모형시험 기반으로 구한 전 저항의 오차는 약 6.4 %이다. 오차의 원인을 분석하면 다음과 같다. 수치해석과 모형시험 시 워터제트 추진 시스템을 장착하여 유도관과 노즐을 통하여 물 유입과 배출이 가능하였으나, 모형시험은 추진 모터의 부하를 줄이기 위하여 임펠러가 자유회전이 가능한 상태(windmill state)로 진행하였다. 반면 수치해석 시에는 자유회전 구현이 어려워 임펠러를 고정하였다. 격자 체계 의존성 시험 대상의 축척 오차도 존재한다. 실제 장갑차의 정성적인 저항 수준을 확인하기 위한 목적으로 격자 의존도 시험을 수행했기 때문이다.
상기의 오차 원인을 비롯하여, 상륙돌격장갑차의 모형시험 결과에 대해 선박의 저항성능에 관한 실선확장법을 적용하여 실차 저항을 추정하는 과정에서 추가적인 오차가 발생할 수 있다. 이러한 오차 요인들에도 불구하고 상륙돌격장갑차용 워터제트 추진기의 설계 시 적정 요구 추력의 산출, 설계 속력에 적합한 주 기관 동력의 범위 결정 등 신규 상륙돌격장갑차의 개념 설계를 위해서는 저항 수준에 대한 초기 분석이 필수적이다. 따라서 상륙돌격장갑차에 대한 실해역 실차 시운전의 결과가 부족한 상황에서, 해석 결과의 오차가 다소 존재하지만 본 결과가 초기 설계 단계에서 실차 크기 상륙돌격장갑차의 저항 수준 추정이라는 해석 목적에 부합한다. 따라서 저항 및 추진 성능 분석 시에는 본 격자 체계를 기반으로 모형 크기로 축소 해석 후 검증 연구를 수행하였다.
마찰저항에 대해 수치해석 결과와 추정 공식을 이용한 결과를 비교하였다. 마찰저항의 경우, 모형시험에서 별도로 측정할 수 없으므로 ITTC 1957 모형선-실선 저항추정법의 마찰저항 공식과 Froude의 평판 마찰공식[19] 및 Hughes의 평판 최소 마찰저항공식[20]을 이용하여 Fig. 10과 같이 비교하였다.
ITTC 1957 마찰저항 추정식은 식 (9)와 같다.
CF는 마찰저항 계수, RF는 마찰저항, S 는 침수 표면적이며, Rn은 선체 길이 및 선속 기반 Reynolds수이다.
Froude의 평판 마찰공식은 1935년에 ITTC에 의해 채택된 후 20세기 중반까지 사용되었으며 식 (10)과 같이 표현된다. λ는 저항계수이다.
Hughes는 평판의 종횡비를 넓은 범위에 걸쳐 변화시켰으며 무한의 종횡비를 갖는 매끄러운 평판의 최소 난류 마찰저항 곡선을 도출하였다.
이상의 결과를 분석하면, 수치해석으로 구한 마찰저항 값은 압력 저항 대비 격자 조밀도 변화에 의한 수치적 소산의 영향을 적게 받는 것으로 나타났다. 일반 상선의 마찰저항 추정에 적합한 ITTC 1957 마찰저항 곡선 대비 상륙돌격장갑차의 마찰저항 해석 결과는 약 25 % 작게 예측하였다. 그 원인은 상륙돌격장갑차가 선미부의 뭉툭한(blunt) 차체 형상에 의해 박리 유동이 발달하므로 압력 저항이 마찰 저항보다 기여도 가 높기 때문인 것으로 분석된다. 마찰저항 추정식 중 Hughes의 평판 최소 마찰저항공식은 통상 선박에 적용 시 추정값이 작게 나오는 경향 때문에 조선 설계 분야에서 활용도가 낮은 편이다. ITTC 1957 모형선-실선 저항추정법의 마찰저항 공식, Froude의 평판 마찰공식 및 Hughes의 평판 최소 마찰저항공식 중 본 상륙돌격장갑차의 전산유체역학 기반 수치해석 결과의 마찰저항 값과 비교할 때 가장 근접한 결과는 Hughes 의 평판 최소 마찰저항공식으로 확인되었다. 따라서 선박 대비 마찰저항의 기여도가 낮고 육상 기동을 위해 선저가 평판 형태인 상륙돌격장갑차의 초기 개념설계 단계에서 수치해석 없이 마찰저항 수준을 추정하고자 할 때, Hughes의 평판 최소 마찰저항공식을 우선적으로 활용 가능하다.
3.3 반활주형 상륙돌격장갑차의 저항 분석
상륙돌격장갑차의 정수 중 저항을 분석하였다. 격자 의존도 시험이 완료된 실차 크기의 격자 체계를 모형 크기로 변환하였으며 격자수는 5.39×106개이다.
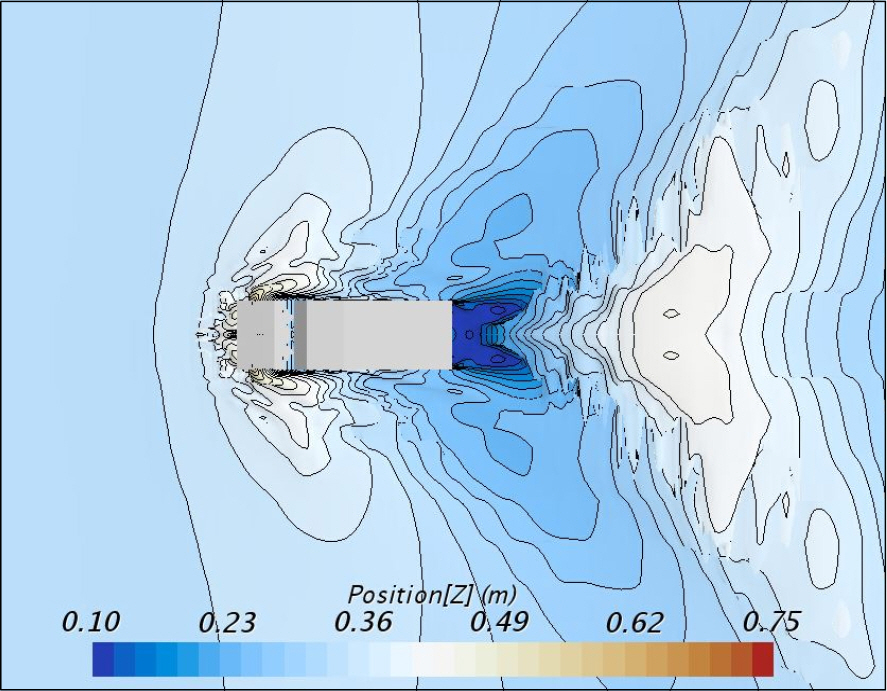
해석 시 시간 간격(time step)은 0.02357초로 하였으며, 총 해석 시간은 300초로 하였다. 주어진 해석 시간 내에서 저항 및 항주 자세의 수렴성이 의도한 기준 이하로 변동 시 수렴하였다고 판단하였다. 판단 기준으로 저항의 경우 평균 저항의 3.3 % 수준에서 비정상 해석 결과가 변동할 경우로 하였으며, 종경사각과 부상량은 각각 0.5도, 0.05 m 수준으로 설정하였다. 정수 중 모형 장갑차의 조파 형상과 계산된 총 16개 해상속력별 저항 곡선을 각각 Fig. 11과 Fig. 12에 도시하였다.
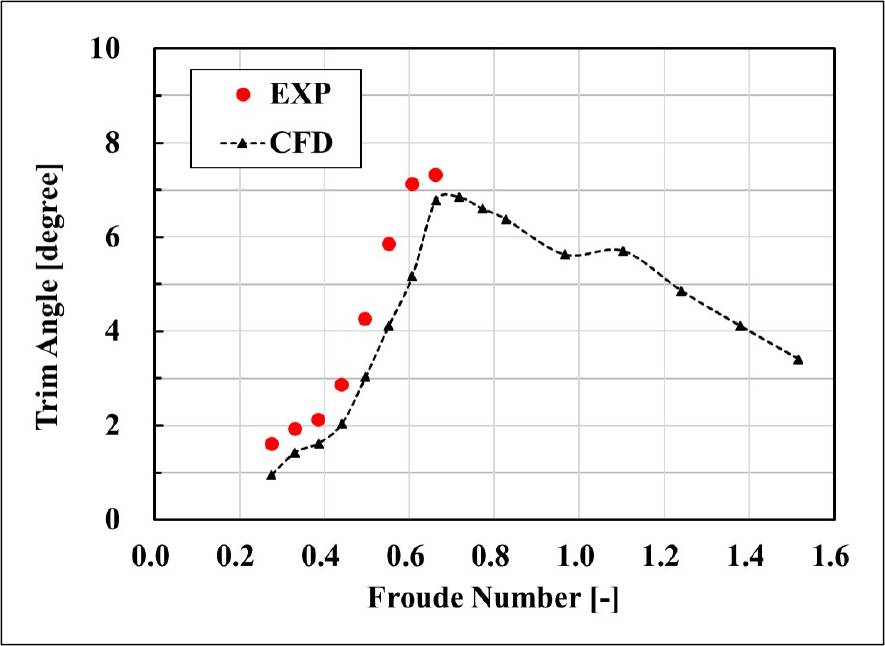
모형시험 계측은 Froude수 0.276에서 0.662까지 수행되었으며, 해당 속력 구간에서 수치해석과 모형시험 간 저항 곡선의 증가 경향은 유사하였다. 고속 구간까지의 수치 분석 결과, Froude수 0.607 이상에서 저항 곡선 기울기의 변화가 시작되어 Froude수 0.662 부근에서 전 저항이 증가하다가 그 이후에는 해상 속력 증가 시 저항 곡선이 수렴하는 경향을 나타내었다. 이는 반활주형 선체의 험프 저항 특성과 유사하며 그 원인은 선수 횡파와 선미 횡파의 중첩에 기인하는 것 이다. Fig. 11에 도시한 Froude수 0.662에서의 파형을 보면, 선수 횡파의 파정이 선수부에 생성되고 선수 횡파의 파골은 선미부에 위치하므로 선미에서 생성된 선미 횡파의 파골과 일치하는 것을 확인할 수 있다.
수치해석과 모형시험 간 평균 오차는 약 7.2 %이며 오차의 원인은 다음과 같이 분석된다.
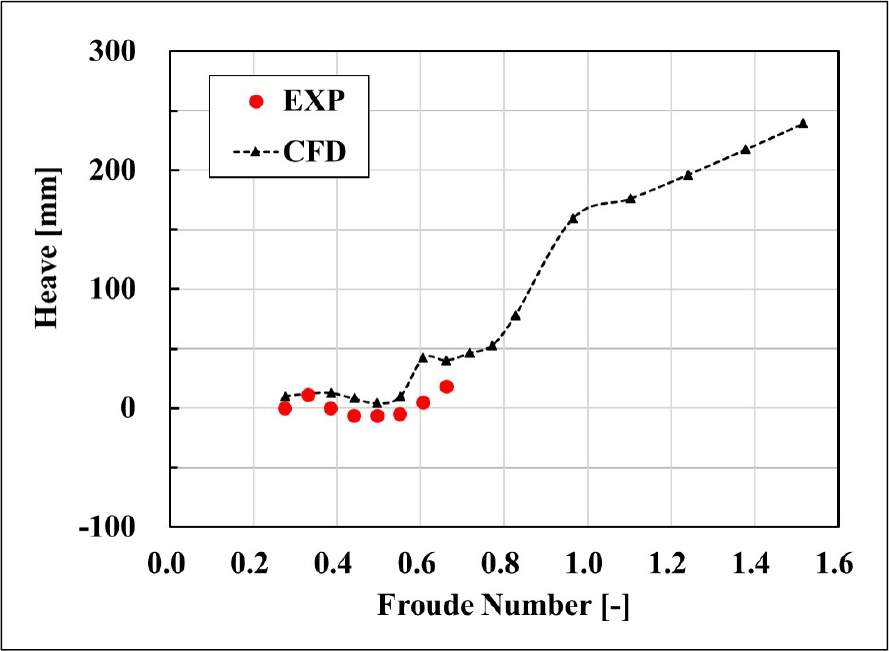
첫째, 종경사각과 부상량 등 자세 변화에 기인한 저항 오차이다. 상륙돌격장갑차는 일반 상선과 달리 해상속력에 따른 항주 자세의 변화가 심하여 형상 저항이 달라지며, 전체 저항의 변화에도 영향을 미치게 된다. 저항 곡선과 대응되는 해상속력별 반활주형 상륙돌격장갑차의 종경사각과 부상량을 각각 Fig. 13과 Fig. 14에 나타내었다. 종경사각은 6.8°를 정점으로 속도 증가에 따라 서서히 감소하여 자세가 안정적으로 개선되고 있다. 종경사각의 경우 모형시험 결과와 해상속력 증가에 따른 경향성은 부합하나 평균 0.99°의 차이를 보였다. 수치해석 결과, Froude수 0.8 이상의 구간에서 부상량은 해상 속력의 증가에 따라 지속적으로 증가하는 것으로 예측되었다. 부상량의 증가는 침수 표면적의 지속적인 감소를 의미하므로, 상기 속력 구간에서의 저항 곡선은 Froude수 0.8 이하 속력 구간의 저항 곡선과 달리 해상 속력의 증가에 따른 저항의 증가 추세가 감소한 것으로 분석된다. 부상량은 Froude수 0.6 부근의 해석결과를 제외하고 전체적으로 수치해석 결과와 모형시험 결과의 경향성이 일치하며, 그 차이는 평균 8.6 mm이다.
오차의 둘째 원인은 격자 의존도 분석 시 언급한 바와 같이 모형시험 시 추진축 구동장비의 손상 방지를 위하여 무부하 자유회전 상태로 두었으나, 수치해석 시에는 고정 상태로 두었기 때문에 고정된 워터제트 임펠러 및 스테이터(stator)에 의해 저항이 증가한 것으로 분석된다. 전체적으로 상륙돌격장갑차의 저항 분석 시 RANS 방정식을 이용한 수치기법의 정확도를 고려할 때 유의미한 수준으로 판단한다.
3.4 배수량형 상륙돌격장갑차의 저항 분석
궤도형 상륙돌격장갑차 중 대표적인 배수량형 선체를 가지는 AAV7A1 장갑차에 대해 실차 크기로 저항 해석을 수행하였다. 해석의 목적은 반활주형 상륙돌격장갑차와의 저항 및 자세 특성의 차이를 비교하기 위함이다.
Fig. 15는 해석에 사용된 상륙돌격장갑차의 표면 격자 형태를 보여준다. 격자 체계는 앞서 기술한 반활주형 장갑차의 격자 의존도 시험 시 사용한 격자 체계 형태로 구성하였다. 공간 격자 체계는 해석의 효율화를 위하여 장갑차의 좌현부만 구현하였다. 전체 격자 수는 약 2.94×106개로 반활주형 격자 체계와 달리 수상 추진 장치의 형상은 구현하지 않았다.
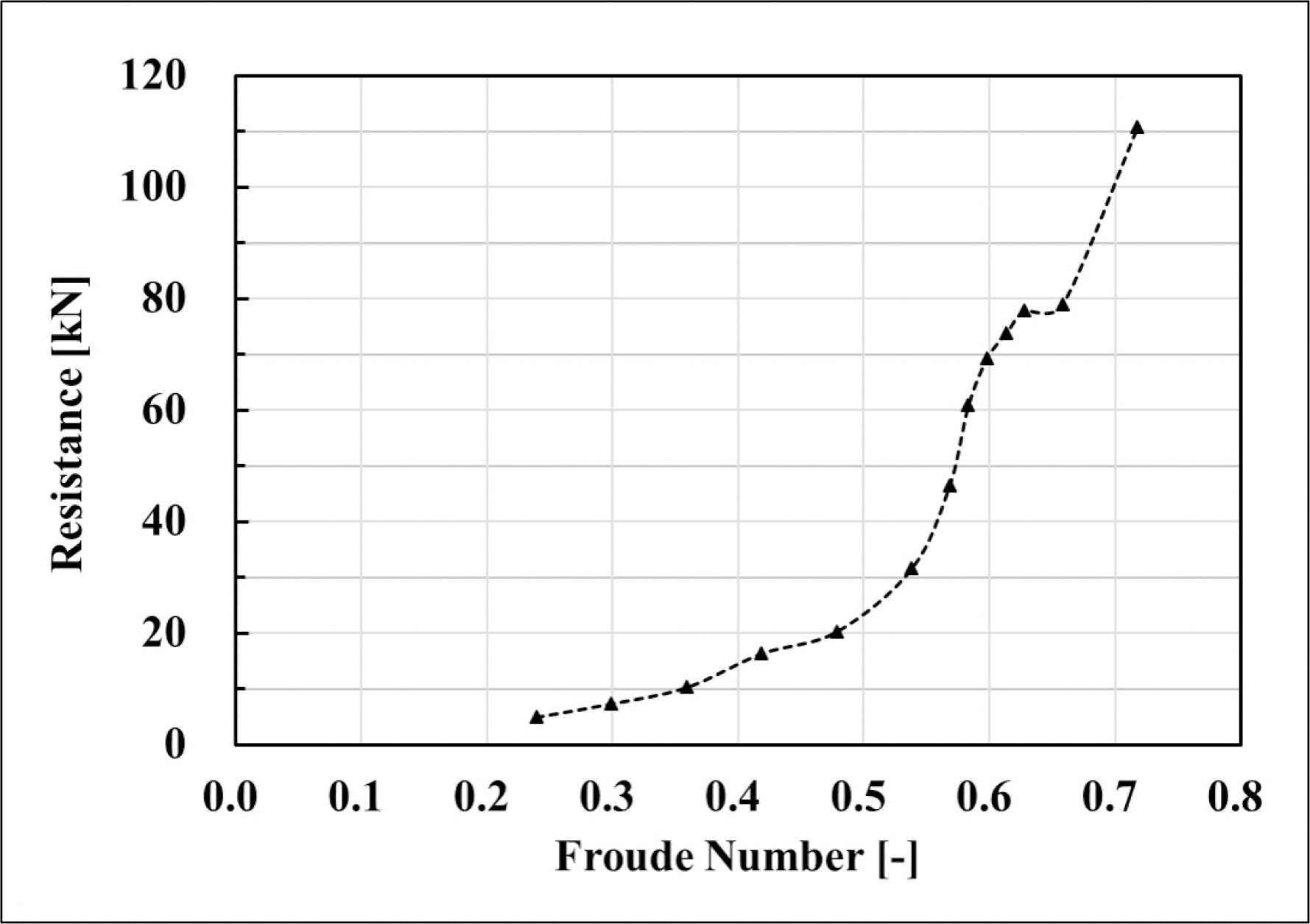
배수량형 상륙돌격장갑차의 저항 해석 결과를 Fig. 16에 도시하였다. Froude수 0.538에서 0.627 부근의 저항 곡선에서 험프 특성이 존재함을 확인하였다. Froude 수 0.583 인근에서 해상 속력 증가에 따른 저항 곡선의 형태가 변하며 전 저항이 크게 증가하였다. 험프 구간 이후에는 조파 저항이 사라지며, 해상 속력 증가에 따라 전 저항이 증가하는 험프 구간 이전의 저항 특성을 나타내었다.
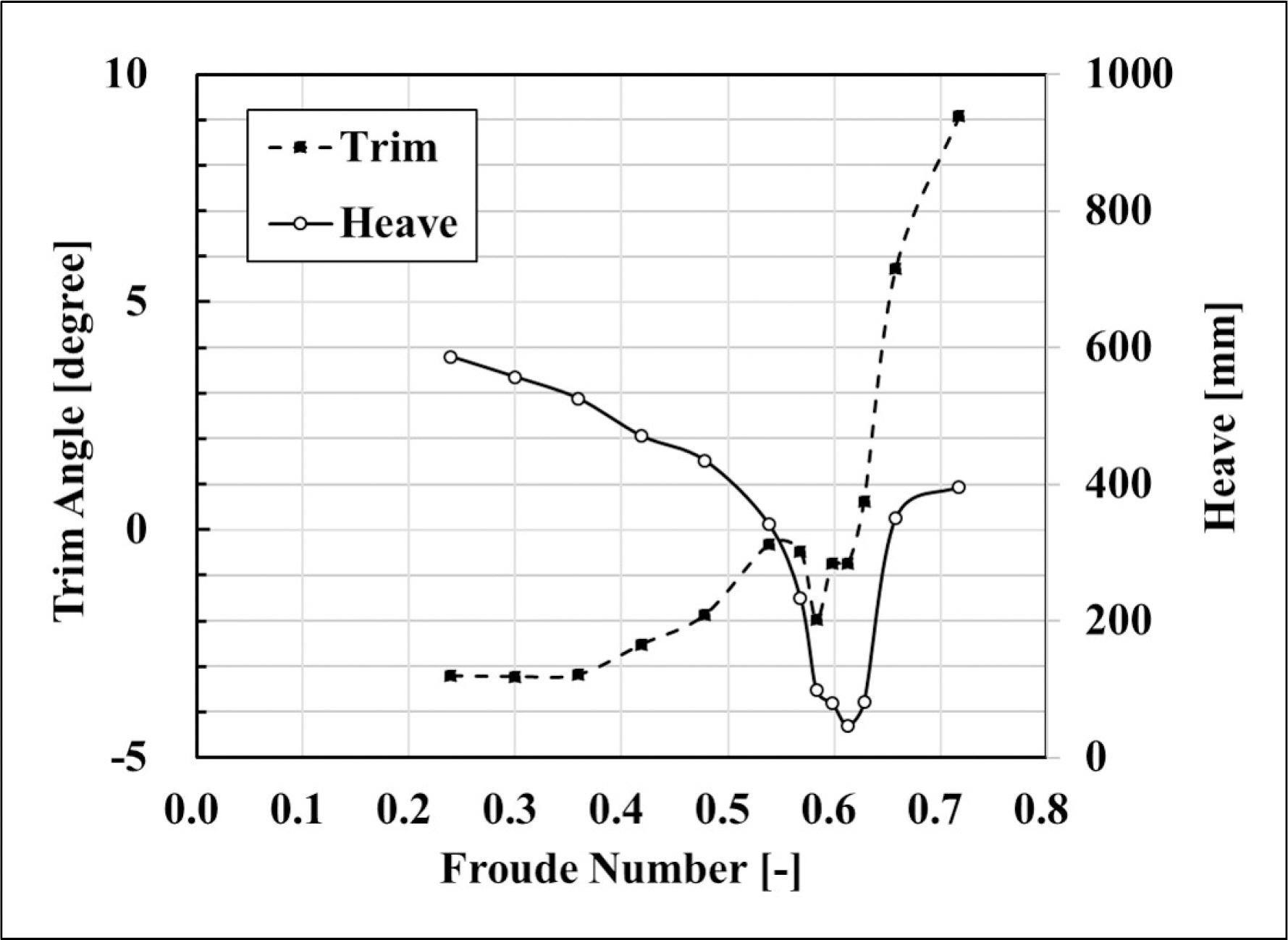
종경사각과 부상량 특성을 Fig. 17에 나타내었다. Froude수 0.239에서 약 3.2°의 선수 트림이 발생하며 험프 구간 전까지 해상 속력이 증가함에 따라 선수 트림이 감소하였다. AAV7A1 장갑차의 특성 상 저속 에서 선수부가 수면 아래를 향하는 수면 돌입 현상(plow-in phenomenon)[21]이 존재하며 저항해석 시 워터제트에 기인한 차체의 부상 효과 등 자세 변경 요인이 제외되었기 때문이다.
험프 특성을 보이는 Froude수 0.538부터 0.627 구간에서 선수 트림이 다시 증가하여 장갑차의 자세가 불안정해진다. 본 속도 영역은 AAV7A1의 해상 최고속도가 약 Froude수 0.4이므로 실제 운용 구간은 아니나, 수면 돌입 현상이 발생할 수 있으므로 고속 항주 시 선수 트림의 발생은 부양 안정성 측면에서 불리하다. 험프 구간 이후의 Froude수 0.658에서는 선미 트림이 약 5.7°로 예측되었으며, Froude수의 증가에 따라 선미 트림도 증가하는 경향을 나타내었다. 과도한 선미 트림은 상륙돌격장갑차의 개념설계 시 선미 트림이 약
4.0° 이상 발생 시 조종수의 전방 시야 확보가 제한되며, 무장 성능 개량 시 기동 간 전방 사격 각도가 제한되어 운용이 어려운 면이 있다. 배수량형 상륙돌격장갑차의 선미 트림은 반활주형 상륙돌격장갑차와 달리 험프 구간 이후에도 증가하는 경향을 보이므로 고속 상륙돌격장갑차용 기본 선형으로는 반활주형이 유리하다.
부상량은 저속 구간부터 험프 특성 구간까지 해상속력이 증가함에 따라 감소하다가, 험프 속력 이후 고속 구간에서는 부상량이 험프 발생 전 수준으로 회복함을 확인하였다.
Fig. 18은 험프 특성 구간이 발생하는 속도 영역인 Froude수 0.583에서의 조파 형태이다. 선수 횡파의 파정은 선수부에 위치하고 파골은 선미부에 위치하며, 선수 횡파의 파골과 선미 횡파의 파골이 일치한 것을 확인할 수 있다. 파골의 중첩에 따라 조파 저항이 급격히 증가하는 험프 특성이 나타난 것으로 분석된다.
4. 자항 성능 평가 결과
4.1 상륙돌격장갑차 및 워터제트 추진 시스템 모델
상륙돌격장갑차의 자항 해석은 반활주형 선체를 대상으로 두 가지 방법으로 수행하였다.
첫째, 자항 성능 해석 기법의 검증을 수행하였다. 모형시험에서 얻어진 표면마찰보정을 고려하지 않은 모형 상륙돌격장갑차의 자항점 속도와 임펠러 회전수 를 입력하고 모형 크기의 수치해석을 수행하였다.
둘째, 본 연구에서 검증된 자항 성능 해석 기법을 바탕으로 궤도 측면 덮개의 적용 유무에 따른 자항 성능의 변화를 평가하기 위한 해석을 수행하였다. 정해진 속도에서 자항점 근처의 회전수 몇 개에 대해 자항 해석을 수행한 뒤, 내삽법을 이용하여 자항점에서의 물리량을 산출하는 방법으로 수행하였다.
4.2 자항 성능 분석 방법
자항 해석에 사용된 격자의 총 제어체적 수는 약 1.69×107개로 회전 영역은 4.5×106개, 중첩격자와 배경격자를 포함 영역은 1.24×107개의 격자로 구성하였다. 계산 영역의 유입 경계면은 차체로부터 차체 길이의 1.5배, 압력 유출 경계면은 차체 길이의 2.5배 그리고 대칭 경계조건으로 경계면은 장갑차 좌현 및 우현으로부터 차체 길이의 1.5배에 해당하는 거리를 두었다. 상·하부 경계면 및 원방 경계면은 차체 길이의 2배에 대응되는 거리를 두었다. 계산비용의 절감을 위하여 장갑차의 우현만 해석하였다.
수치해석 방법은 임펠러의 회전 운동을 제한하고 장갑차 자세를 고정한 상태에서 비정상 해석을 충분히 수행하여 계산의 안정성을 확인한 후 장갑차 자세의 구속을 먼저 해제하였다. 임펠러가 정지 상태에서 서서히 구동을 시작하여 최대 회전수에 도달한 후 추력, 토오크 및 항주 자세가 일정하게 수렴된 거동을 보이는 시간까지 해석을 수행하였다. 계산 시간 간격은 0.05초이다.
자항 해석 결과를 바탕으로 임펠러의 추력 계수 KT, 토오크 계수 KQ, 유량 계수 JQ 및 준 추진효율(quasi-propulsive efficiency) ηD의 산출을 통하여 추진 성능을 평가하였다. 각 계수들의 정의는 다음과 같다.
T는 임펠러의 추력, n은 임펠러의 초당 회전수, D는 임펠러의 직경을 나타내며, TQ는 임펠러의 토오크, Q 는 워터제트 추진 시스템의 유량을 의미한다.
PE는 유효마력(effective horse power)이며, PD는 전달마력(delivered horse power)이다. 유효마력은 장갑차가 해상에서 기동 시, 전 저항(RT)을 받으며 일정한 차속(vehicle speed, VS)으로 기동할 때 필요한 요구되는 동력을 의미한다. 본 논문에서는 수치해석으로 구한 장갑차의 자항추진 시 전 저항과 입구 경계조건에서 부여한 장갑차의 해상 속력을 이용하여 유효마력을 계산하였다. 전달마력은 주 기관으로부터 변속기와 유니버설 조인트를 거쳐 수상 구동축을 통해 임펠러에 순수하게 전달된 동력을 의미하며, 계산 조건으로 부여한 임펠러의 회전수와 계산된 임펠러의 토오크 값으로 산출하였다.
4.3 자항 해석 결과 및 검증
Froude수의 변화에 따른 추진 성능 계수를 수치 분석을 통하여 산출하였다.
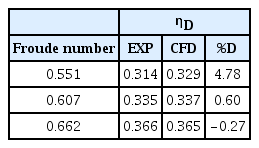
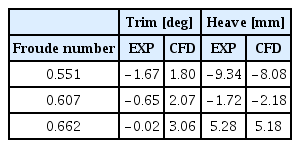
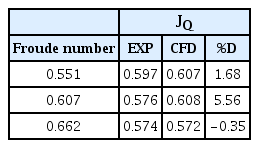
임펠러 추력 계수, 임펠러 토오크 계수, 워터제트 추진 시스템의 유량 계수 및 준 추진 효율을 각각 Table 4에서 Table 7까지 나타내었다. 모형시험 결과와 비교하여 수치해석의 오차를 함께 도시하였다. 항주 자세는 계산이 수렴된 후 계산이 종료될 때까지의 종경사각과 부상량의 평균값을 대표값으로 산출하였으며 Table 8에 나타내었다.
해상 속력별 자항 해석 결과에서 자항점의 추력 계수값은 Froude수 0.551에서 약 5.11 % 오차를 나타내었으며, 속력이 증가함에 따라 1.85 % 수준으로 감소하였다. 토오크 계수도 Froude수 0.551에서 약 4.76 % 오차가 발생하였으나, Froude수 0.662에서는 약 1.89 %로 감소하였다. 유량 계수는 Froude수 0.607에서 다소 오차가 증가하지만 Froude수 0.662에서는 실험치와 비교할 때 타당한 결과를 나타내었다.
수치해석으로 얻어진 자항 추진 시 전 저항과 차속 그리고 임펠러의 토오크를 이용하여 워터제트 추진 시스템의 준 추진효율을 계산하면 Froude수 0.551에서 약 0.329, Froude수 0.607에서 약 0.337, Froude수 약 0.662에서 0.365 수준으로 분석되었다. 이는 모형시험 결과의 준 추진효율인 Froude수 0.551에서 약 0.314, Froude수 0.607에서 약 0.335, Froude수 0.662에서 약 0.366의 수치와 잘 부합하는 결과이다. 고속에서 오차가 감소하는 원인은 장갑차의 항주 자세와 관련이 있는 것으로 분석된다. 종경사각과 부상량은 전체적으로 Froude수가 증가함에 따라 오차가 감소하는 것으로 파악되며 Froude수 0.662 이후로 장갑차가 부상하면서 안정적인 항주 자세를 유지하므로 수치해석과 모형시험 간 오차가 감소한 것으로 추정한다.
상기 결과를 기반으로 본 논문에서 활용한 전산유체역학 기반 수치 분석 기법은 워터제트 추진 시스템을 장착한 고속 상륙돌격장갑차의 추진 성능, 항주 자세 및 효율 분석 시 모형시험과 비교하여 타당한 추정 정도를 보이고 있다. 따라서 본 수치해석 기법이 초기 설계 단계에서 자항 성능 분석 시, 정성적인 우열을 결정하고 추진 성능을 수치화하여 평가하는데 유용하게 사용될 수 있을 것으로 판단한다.
4.4 궤도 측면 덮개 적용 시 추진 성능 변화 분석
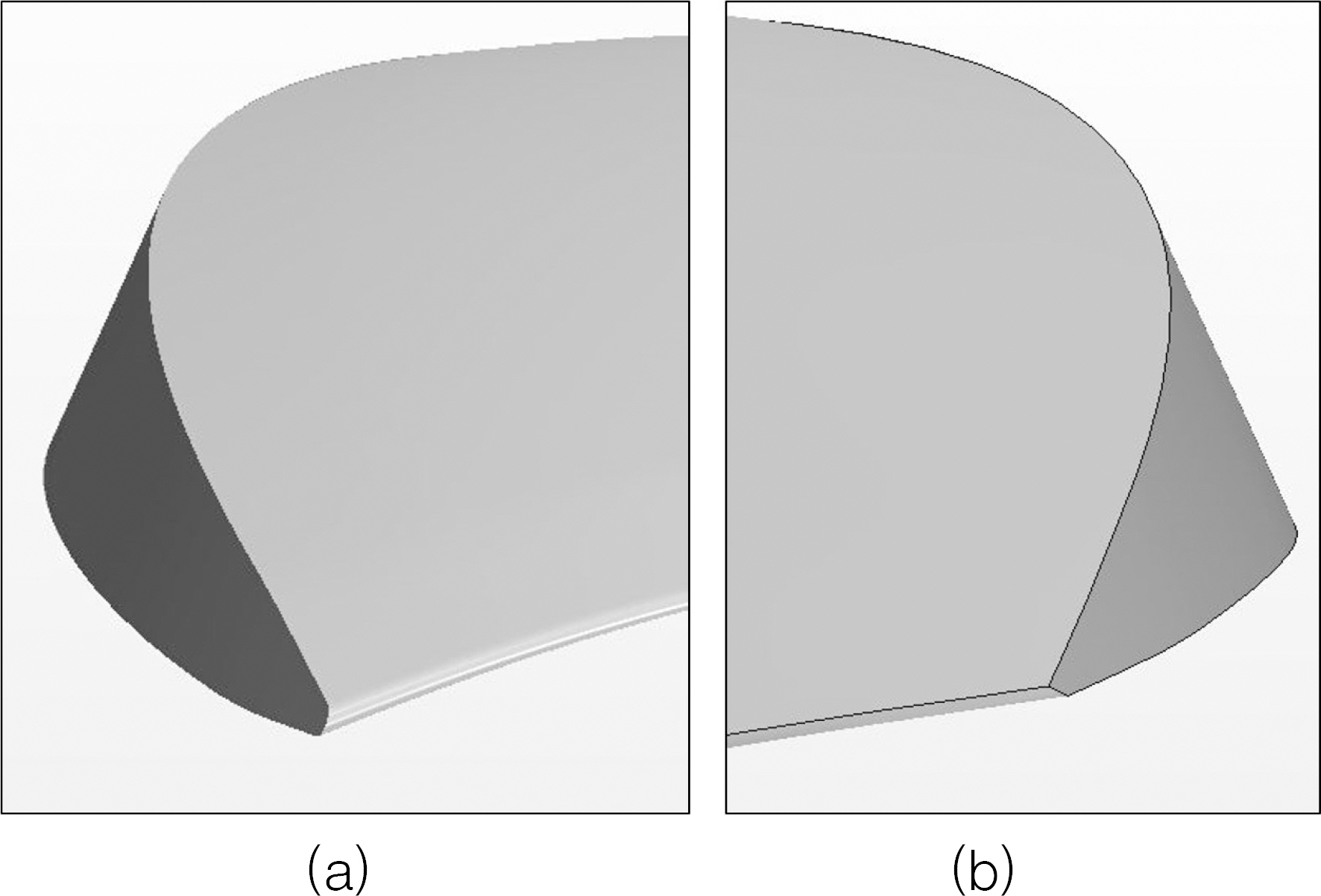
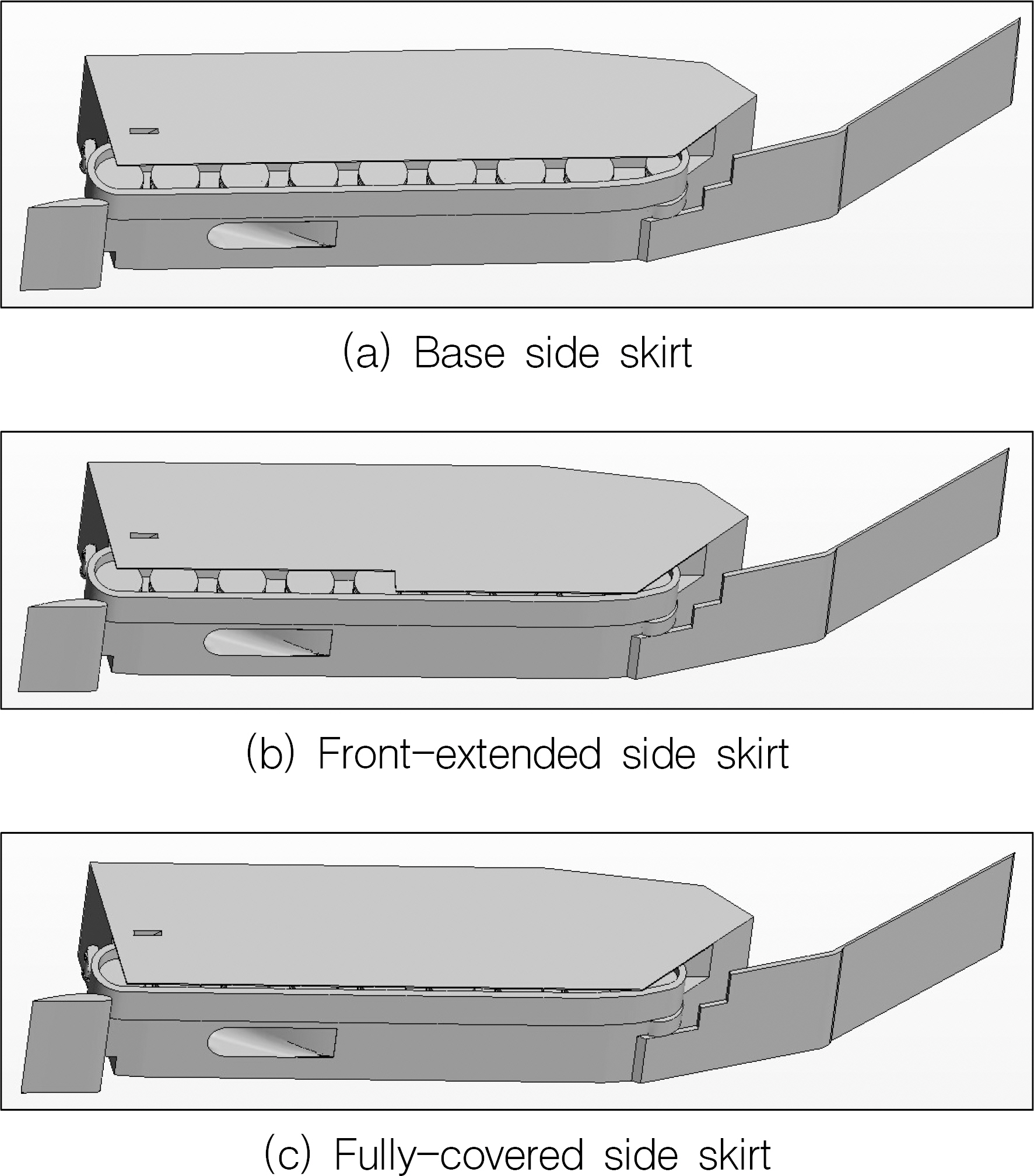
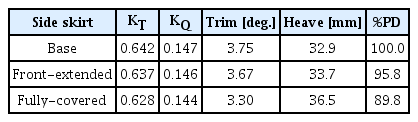
상륙돌격장갑차의 궤도 측면에는 덮개 형태의 판재가 적용되어, 차량 하부 측면의 방호력을 제공하며 궤도에 의한 수상 저항을 감소시키는 역할을 한다. 궤도 측면 덮개의 길이별 형상을 Fig. 19에 도시하였다. Fig. 19 (a)는 일반적인 장갑차와 유사한 수준으로 궤도 측면 덮개의 길이를 설계한 결과이다. 해상 기동을 위하여 궤도를 수납한 상태에서도 차륜의 일부가 노출되어 있는 구조이다. Fig. 19 (b)는 현용 상륙돌격장갑차의 원형인 AAV7A1과 같이 궤도의 전방부를 덮을 수 있도록 궤도 하단까지 측면 덮개 중 일부만 적용한 것이다. Fig. 19 (c)는 측면 덮개를 전체 궤도의 하단부까지 확장하여 해상 기동 시 궤도를 모두 가릴 수 있는 형태이다. 세 경우에 대하여 측면 덮개의 형상을 제외하고, 워터제트 추진 시스템의 형상 및 수상 운행 장치의 설치 각도 등 기타 조건은 동일하다. 또한, 측면 덮개의 형상에 따른 장갑차의 총 중량과 관성 모멘트의 변화는 무시하였다. 본 절에서 사용된 반활주형 상륙돌격장갑차의 형상은 3.3절에서 저항 분석 기법의 검증을 위해 활용된 차체 형태와 동일하다. 본 연구에 서 계산 시간은 추력과 토오크 및 항주 자세가 일정하게 수렴된 거동을 보이는 시간까지 수행하였으며, 수치해석은 모형 자항 시험 절차와 동일하게 추정 자항점 주위로 임펠러의 회전수를 변화시켜 가면서 추력과 전 저항이 일치하는 지점에서 자항점을 구하였다.
Table 9는 Froude수 0.634에서 궤도 측면 덮개의 형태에 따른 자항 성능 분석 결과를 비교한 것이다. 측면 덮개를 전방만 확장하였을 경우에는 동일한 해상 속력을 달성하기 위한 임펠러의 추력 계수와 토오크 계수가 감소하여, 유사 장갑차 수준의 궤도 측면 덮개를 적용한 기본 형상 대비 전달 마력이 약 4.2 % 감소한 것으로 분석되었다. 궤도 측면을 완전히 덮는 형태의 측면 덮개를 적용한 경우에는 기본 형상 대비 전달 마력이 약 10.2 % 감소하였으며 종경사각은 약 0.45° 감소하고 부상량은 약 10.9 % 증가하였다.
따라서 궤도 측면을 완전히 덮는 형태의 측면 덮개를 적용하면 체계 전체 중량은 다소 증가하지만, 고속 해상 기동 시 침수 표면적 감소로 수상 저항 측면에서 유리해지며 종경사각 감소로 기동 간 포 사격 시 안정적인 자세 유지가 가능할 것으로 판단한다.
5. 결 론
RANS 방정식 기반 해석을 통해 고속 해상 기동을 실시하는 상륙돌격장갑차의 저항 및 추진 성능을 분석할 수 있는 수치기법을 정립하였다. 장갑차 주위 자유 수면 효과와 동적 유체 구조 상호작용을 고려하여 중첩 격자 시스템을 적용 후 장갑차의 해상 기동 시 운동 해석을 수행하였다.
반활주형 상륙돌격장갑차의 저항을 수치해석 기법으로 분석하고 모형시험 결과와의 검증을 통해 비교적 타당한 일치를 확인하였다. 저항 추정 오차 중 수상 속력에 따라 종경사각과 부상량의 변화에 기인하는 요소에 대해서는 추가 연구가 필요하다. 검증된 수치해석 기법으로 배수량형과 반활주형 상륙돌격장갑차에 대해 해상 속력별 저항 특성과 항주 자세를 해석하여 험프 특성 구간을 포함한 저항 곡선을 분석하였으며, 험프 속력에서 조파 형태를 해석하여 조파 이론과의 타당한 연계성을 확인하였다.
반활주형 상륙돌격장갑차의 자항 해석을 수행하고 모형시험 결과와 비교하여 설계 Froude수에서 약 1.85 % 수준의 추력 오차로 일치성을 확인하였다. 따라서 기본 설계 시 정성적인 우열을 결정하고 초기 추진 성능 추정 하는 목적으로 사용 가능하다. 검증된 자항 해석 기법을 이용하여 궤도 측면 덮개의 설계안에 따른 자항 성능 및 항주 자세에 미치는 영향을 분석하였다. 일반적인 장갑차 계열에 적용한 측면 덮개의 길이를 연장하여 궤도의 대부분을 가리는 형상을 적용할 경우, 설계 Froude수에서 전달 마력을 약 10.2 % 정도 절감 가능하며 안정적인 항주 자세를 확보할 수 있을 것으로 평가한다.
추후 본 연구의 분석 기법에 기반하여 실차 크기 장갑차를 대상으로 해석을 수행하고 체계 시운전 결과를 바탕으로 검증을 수행하고자 한다. 또한, 상륙돌격장갑차의 파랑 중 저항 및 추진 성능 분석을 통해 탐색 및 체계 개발 시 설계에 활용하고자 한다.