|
 |
- Search
| J. KIMS Technol > Volume 25(3); 2022 > Article |
|
Abstract
Mine detection has been mainly studied with images of the forward-looking sonar. Forward-looking sonar assumes the propagation path of the sound wave as a straight path, creating the surrounding images. This might lead to errors in the detection by ignoring the refraction of the sound wave. In this study, we propose a mine localization method that can robustly identify the location of mines in an underwater environment by considering the refraction of sound waves. We propose a method of estimating the elevation angle of arrival of the target echo signal in a single receiver, and estimate the mine location by applying the estimated elevation angle of arrival to ray tracing. As a result of simulation, the method proposed in this paper was more effective in estimating the mine localization than the existing method that assumed the propagation path as a straight line.
기뢰는 손쉽게 부설 가능하고 적이 접근할 때 까지 대기하여 공격하는 해군 무기체계이다. 한번 부설된 기뢰는 폭발하기 전까지 기뢰 존재여부 및 위치를 추정하기 어려워 소해에 많은 위험이 동반되므로 기뢰탐지연구에 대한 중요성이 부각되고 있다[1]. 기뢰 탐지에 대한 연구는 측면주사소나(Side Scan Sonar, SSS), 전방주시소나(Forward Looking Sonar, FLS)등으로 획득된 소나 이미지를 이용하여 탐지하는 방법이 주로 연구되었다[2,3]. 국내에서는 전방주시소나의 하드웨어 개발연구가 활발히 진행되고 있으나[4], 전방주시소나를 이용하여 기뢰를 탐지하는 방법론에 대한 연구는 미비한 실정이다. 전방주시소나는 단상태 능동소나로써 신호를 송신하고 표적으로부터의 반향음이 수신기에 수신되는 시간을 측정하여 표적의 거리를 추정한다. 전방주시소나의 수신기로부터 획득되는 소나 이미지는 일반적으로 음파의 전달경로를 직선으로 가정하여 전 방을 방위와 수심에 대한 격자로 나눈 후 각 격자에서 반사 또는 산란된 음파 세기를 표현하여 이미지를 만든다[5]. 하지만 이는 음파의 전달경로를 직선 경로로 가정하였기 때문에 음속구조에 의한 음파의 굴절현상은 반영하지 못한다. 해양환경은 시공간적으로 달라지며 음속구조의 변동성을 야기한다. 해양환경에서 전달되는 음파는 음속이 빠른 곳에서 느린 곳으로 굴절하는 현상이 발생하며, 이러한 음파의 굴절현상에 의하여 추정된 기뢰의 거리와 수심에 오차가 포함될 수 있다. 소나를 이용한 표적 위치 추정 연구는 주로 수동 수직 수신기배열을 이용하여 표적의 위치를 추정하는 기법으로 연구되었다. 빔형성 기법을 이용한 정합장처리 기법(Matched Filed Processing, MFP), 차주파수 빔형성, 압축센싱 빔형성, 배열 불변성 등 다양한 기법이 연구되었으며, 국내에서는 다중경로의 입사각과 시간지연 값을 이용하여 표적의 심도를 추정하는 기법이 연구되었으나, 표적의 거리는 알고 있다고 가정하였다[6–12]. 하지만 전방주시소나의 구조처럼 수직 송신기 배열과 수평 수신기 배열의 broadside 방향에서 표적의 위치를 추정하는 연구는 미비한 실정이다. 따라서 본 논문에서는 수중에 계류된 기뢰를 탐지하는 상황을 가정하여, 음속구조에 따른 음파의 굴절현상을 반영한 계류기뢰의 위치를 추정하기 위한 연구를 수행하였다. 이를 위해 전방주시소나의 원시데이터인 기뢰표적의 반향신호를 모의하고 신호처리 과정을통해 기뢰표적 반향신호 탐지 및 기뢰 표적의 위치인 거리와 수심을 동시에 추정하는 알고리즘을 제안한다.
본 논문의 구성은 다음과 같다. 2장에서 전방주시소나의 구조 및 송신신호, 구성방법과 기뢰 표적 반향신호 모의과정에 대하여 설명하고, 3장에서 제안한 송신각도 추정기법과 기뢰 표적의 거리 및 수심 추정 알고리즘을 설명한다. 4장에서 모의환경에서의 시뮬레이션 실험을 통하여 제안 알고리즘의 성능을 확인하며, 5장에서 결론을 맺는다.
전방주시소나는 무인수상정, 잠수함 등의 선체 앞에 부착되어 해양에서 기뢰, 어초 등과 같은 전방의 장애물을 식별하고 회피할 목적으로 사용된다. 전방주시소나에서 주파수, 빔폭, 센서구성 등의 사양은 제조업체 및 모델에 따라 다르지만 구조와 작동방식은 모두 유사하다[5].
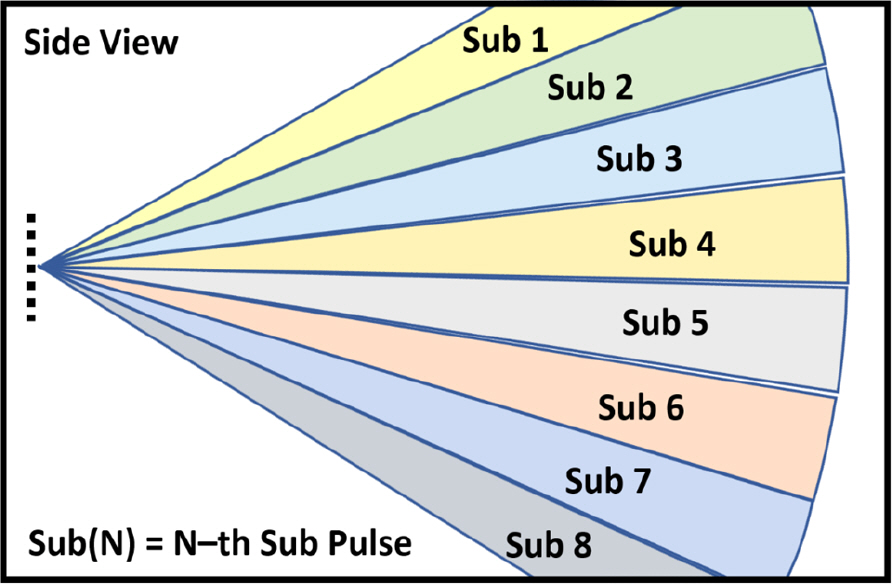
전방주시소나는 Fig. 1과 같이 수직 송신기 배열과 수평 수신기 배열로 구성된다. 송신기 배열에서는 수직 지향각과 주파수가 서로 다른 다수의 부펄스를 송 신하는 방식으로 수신되는 기뢰 표적신호의 수직 도달 각도에 대한 구분이 가능하고, 수신기 배열에서는 수평적으로 수신되는 음파의 시간 차이를 이용하여 방위에 대한 구분이 가능하다. 전방주시소나의 송수신 배열 센서의 개수 및 송신신호 구성방식은 최대 탐지거리 및 거리 분해능에 따라 다르게 구성된다. 본 논문에서는 수직 음속구조를 반영한 기뢰 표적의 거리 및 수심을 추정하기 위하여 방위에 대한 고려는 제외하였다. 따라서 수신기 배열의 broadside 방향에서 표적의 위치를 추정하는 것을 가정하여 수신기는 배열이 아닌 단일 센서로 구성하였고 송신기 배열은 수직 빔폭을 고려하여 20개의 센서로 구성된 배열을 고려하였다.
전방주시소나의 송신신호는 지향각이 다른 8개의 부펄스로 구성하였으며 각 부펄스는 중심 주파수가 서로 다른 선형 주파수 변조신호(Linear Frequency Modulated Waveform, LFM)로 이루어진다. LFM신호는 정합필터(Matched Filter)를 통하여 높은 시간 분해능과 신호 대 잡음비를 획득 가능한 장점이 있다[13].
Fig. 2는 부펄스별 수직 지향각도를 나타낸 모식도이다. 첫 번째 부펄스는 해수면 방향을 지향하고, 마지막 부펄스는 해저면 방향을 지향하도록 빔을 형성하였다. 전방주시소나에서 부펄스 신호는 2.1절에서 설명한 바와 같이 수직 송신기 배열을 이용하여 지향성을 가지는 송신신호를 고각별로 송신하며, 수신한 신호에서 정합필터를 통하여 특정 고각에 대한 반향세기를 판별하는 목적으로 사용된다. Table 1은 각 부펄스에 적용한 지향각도 및 주파수를 정리한 표이다. 중심주파수 값은 보안문제로 인하여 표기하지 않았다.부펄스별 송신신호는 LFM 신호에 중심주파수를 각각 다르게 적용하였고, 신호길이(Pulse Length)를 10 ms, 밴드 폭(Band Width)을 1 kHz로 설정하였다. 전방주시소나의 송신방식은 부펄스 1번 신호부터 8번까지 차례대로 송신하며, 부펄스 1번 신호를 송신 후 다음 부펄스 신호를 송신할 때까지 대기시간을 갖는다. 이는 송신각도를 변경하기 위함이며 본 논문에서는 부펄스 신호 송신 후 대기시간을 5 ms로 설정하였다.
전방주시소나에서 기뢰표적 반향신호의 모의과정은 기뢰표적에 대한 응답함수를 도출하여 부펄스별 송신신호와 합성곱(Convolution)연산을 수행하여 표적신호를 모의한다. 이후 Wenz curve 모델[14]을 이용하여 모의된 백색 가우시안 소음신호와 시계열 합을 이용하여 기뢰표적 반향신호를 모의하였다. 표적신호의 응답함수는 고유음선 추적 과정으로 계산된 전달시간과 소나방정식에 의해 계산된 수신준위를 통합하여 모의하며, 각 부펄스별 수신 준위를 계산하기 위한 소나방정식은 다음과 같다.
능동소나에서 송신된 신호가 표적에서 반향되어 수신기로 수신된 준위를 수신준위 RL(Received Level)이라고 하며, N은 N번째 부펄스에 대한 값을 의미한다. 음원준위는 SL(Source Level), 확산손실 TLsp(Spreading Loss)와 흡수손실 TLab(Absorption Loss)의 합을 전달손실 TL(Transmission Loss)이라고 한다. TS(Target Strength)는 표적강도, BP(Beam Pattern)는 송신배열의 빔패턴, NL(Noise Level)은 주변소음 준위를 의미한다. 본 연구에서 전달거리, 전달시간, 확산손실 및 송신기에서 표적으로 음파가 전파되는 음선의 송신 고각과 표적에서 수신기로 도달하는 표적신호의 수신 고각은 음선이론기반의 BELLHOP 모델[15]을 통하여 계산하였고, 흡수손실은 Thorp 감쇠모델[16]을 적용하였다. 기뢰표적은 반경이 2 m인 구형형상의 점표적을 가정하여 표적강도를 모의하였다[17]. 전방주시소나의 송신 빔패턴은 각각의 송신기가 등방성 파형을 갖는다고 가정하여 다음과 같은 식 (2)로 계산하였다[18].
식 (2)에서 Narray는 송신기 배열의 센서 개수, K는 파수, d는 송신기 배열의 센서 간격, θ는 송신 고각, θs(N)은 부펄스별 지향각도, ∆Φ는 각 송신기 센서들의 위상 차이를 나타낸다. 본 연구에서는 전방주시소나의 송신기 수직배열을 20개의 센서로 가정하였고, 송신기의 간격 d는 송신 부펄스의 최대 중심 주파수인 F8의 λ/2 간격으로 설정하였다[18].
기뢰표적 응답함수의 수신준위 모의과정은 다음과 같다. 먼저 음원준위를 설정한 뒤 전방주시소나로부터 기뢰표적까지의 고유음선 추적을 통하여 전달거리, 확산손실, 송신 고각을 계산한다. 본 연구에서 전방주시소나 송수신 시간 내에 해양환경의 변동성은 없다고 가정하였다. 따라서 송신기에서 표적으로 음파가 전파되는 음선의 송신 고각과 표적에서 수신기로 도달하는 표적신호의 수신 고각은 동일하게 모의하였다. 모든 부펄스에서 전달거리와 확산손실은 고려한 주파수 대역 내에서 차이가 충분히 작다고 가정하여 같은 값으로 모의하였다. 고유음선추적을 통하여 계산된 전달거리에 각 부펄스의 주파수별 감쇠계수를 곱하여 흡수손실을 계산하고, 부펄스의 주파수와 지향각도를 이용하여 빔패턴을 모의하였다. 이후 표적강도를 계산하여 위의 소나방정식에 적용하는 방식으로 기뢰표적 응답함수의 수신준위를 모의하였다. 수신준위와 송신신호를 합성곱(Convolution) 연산을 통하여 기뢰표적 반향신호를 모의하였다.
본 논문에서 제안하는 알고리즘은 전방주시소나에서 기뢰표적 반향신호를 모의 및 탐지하여 기뢰표적 반향신호의 전달시간과 수신 고각을 추정하는 것이며, 이를 음파전달모델에 적용하여 계산함으로써 표적의 위치 추정하는 기법이다.
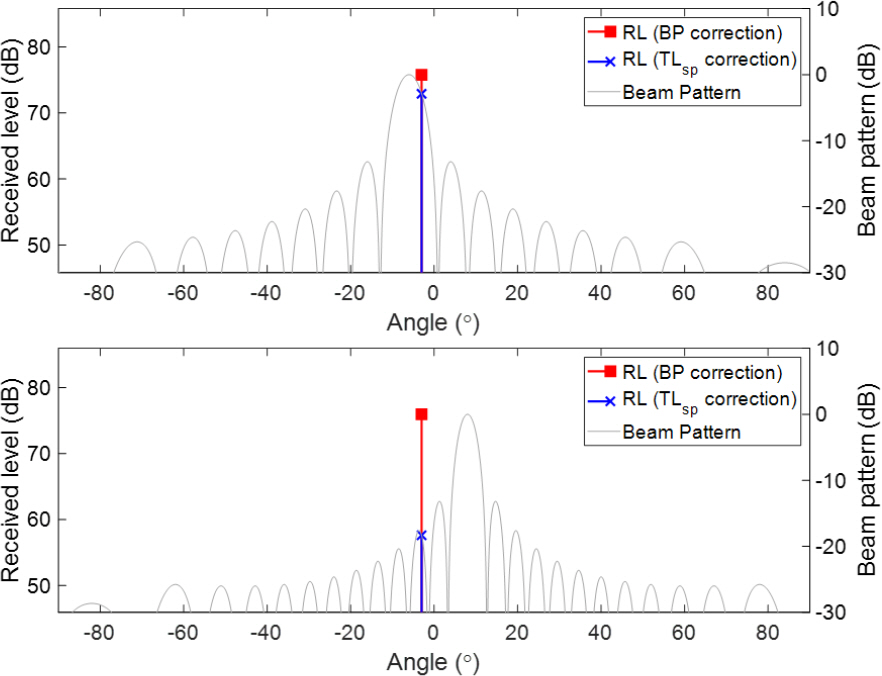
Fig. 3은 기뢰표적에 대해 부펄스별로 모의된 반향신호에서 수신 고각을 추정하기 위한 과정을 나타낸 그림이다. 먼저 반향신호에서 송신신호로 정합필터를 수행하여 신호 대 잡음비를 높이고 주변소음으로부터 신호를 구분한다. 이후 부펄스별 주파수에 따른 흡수손실과 지향한 각도에 따른 빔패턴을 보정하게 되면 소나방정식 상 남은 파라미터는 음원준위, 전달손실과 표적강도로 모든 부펄스에서 동일한 준위를 가진다. 이러한 특징을 이용하여 부펄스별 기뢰표적 반향신호에 종속적인 파라미터를 보정해줌으로써 기뢰표적신호 수신 고각을 추정한다.
전방주시소나에서 기뢰표적신호 수신 고각 도출을 위한 자세한 과정은 다음과 같다. 기뢰 표적의 전달시간과 수신준위를 결정하기 위해서 모의된 수신신호에 부펄스별 송신신호로 정합필터를 수행한다. 정합필터란 상호상관관계(Cross correlation)를 이용하여 송신 펄스의 복제신호(Replica) 상관도로부터 상관도가 높은 표적 반향신호는 높이고, 상관도가 낮은 소음 신호는 감소시킴으로써 높은 신호대 잡음비를 보이며 주변소음 준위를 억제시키는 효과를 가진다[13]. 부펄스별 정합필터 결과의 최댓값을 수신준위로 결정하고 최댓값이 수신된 시간을 표적 전달시간으로 결정한다. 표적의 전달시간을 이용하여 전방주시소나 수심의 음속을 곱해줌으로써 대략적인 음파의 이동거리를 예측하고 이를 Thorp 감쇠계수에 곱해줌으로써 흡수손실을 보정한다. 이는 실제 전달거리와 차이가 발생하지만, 모든 부펄스에서 동일한 전달거리 오차가 발생하므로 부펄스별 수신준위의 차이로 추정되는 고각에는 영향을 미치지 않는다. 이후 해수면 방향인 −90 도 고각부터 해저면 방향인 90 도 범위의 모든 고각에 대한 각 부펄스별 빔패턴을 보정한다.
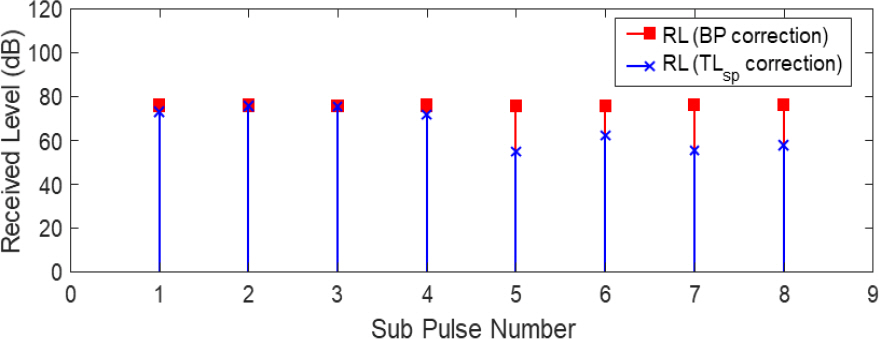
Fig. 4는 부펄스 1번 신호와 부펄스 8번 신호의 빔패턴 보정결과를 나타낸다. 흡수손실이 보정된 부펄스 수신준위에 부펄스별 빔패턴을 계산한 후 고각에 맞는 빔패턴 값을 역으로 더해줌으로서 빔패턴을 보정한다. 이때 보정한 고각과 표적신호 수신 고각이 동일해지면 부펄스에 따른 종속항이 사라지며 Fig. 5와 같이 모든 부펄스의 수신 준위는 동일한 준위를 갖게 된다. 따라서 부펄스별 준위 값의 차이를 목적함수(Object function)로 설정한 뒤 고각을 바꾸어 가면서 빔패턴을 보정하여 목적함수가 최소가 되는 고각을 도출하고 이를 표적의 수신 고각으로 결정한다.
기존 BELLHOP 모델을 통한 고유음선 계산과정은 송/수신기 위치와 표적 위치를 정하고, 송/수신기 위치에서 음선계산을 시작하여 표적 위치에 도달한 음선을 추출하는 방식으로 계산된다. 본 연구에서는 표적신호 음선의 수신 고각과 표적신호의 도달시간으로 고유음선을 계산하는 방법을 적용하여 표적위치를 추정하였다. 수신된 표적신호의 도달시간과 수신 고각에 대한 정보로 표적 위치 추정 시 고유음선추적을 이용한다면 음속구조가 변동하는 해양환경에서 보다 정확한 표적 위치 추정이 가능하다.
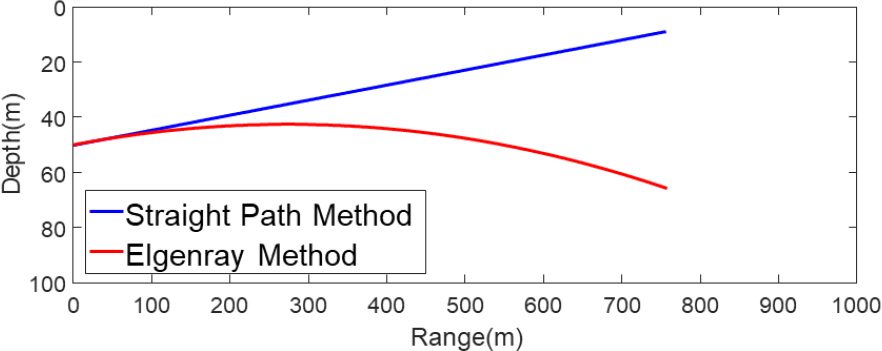
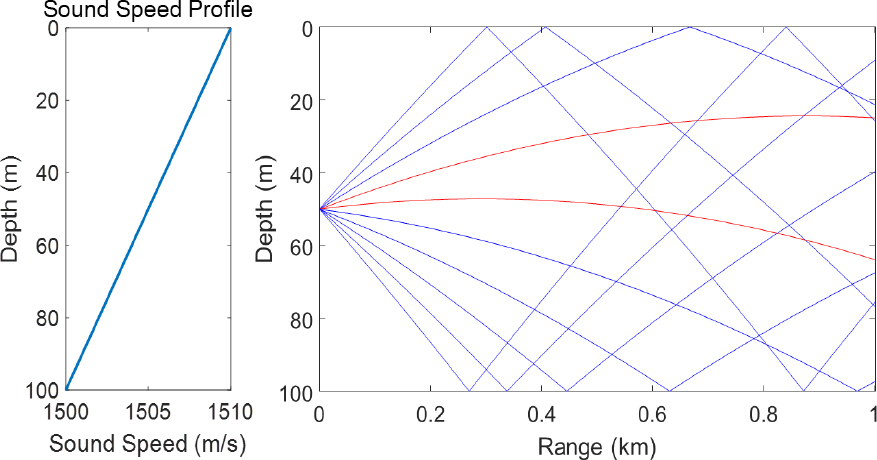
해수면 음속이 1530 m/s 해저면 음속이 1500 m/s로 선형음속구조 환경에서 송수신기 수심 50 m일 경우, 특정 수신 고각으로 기뢰 위치를 직선으로 가정하여 추정한 방법과 음선이론을 적용하여 추정한 방법의 차이를 Fig. 6에 나타내었다. 음속구조 변동성에 의하여 굴절현상이 발생하는 해양 환경에서는 표적 위치에 대한 고각과 직접파가 도달하는 수신 고각이 차이가 발생한다. 음파의 굴절현상을 반영하지 않고 수신 고각에 대한 음파의 전달경로를 단순히 직선으로 가정하면 표적의 거리와 수심 추정 값에 오차가 발생할 수 있다. 또한 음파가 전달되는 거리가 멀어질수록 직선으로 가정한 방법의 기뢰 위치 추정 오차가 커지므로, 음선이론을 적용한 경우에는 거리가 멀어지더라도 음파의 굴절효과를 반영하여 위치를 추정하기 때문에 보다 정확한 기뢰 위치를 추정할 수 있다.
제안한 전방주시소나의 기뢰표적 위치추정 알고리즘의 성능을 확인하기 위하여 모의실험을 진행하였다. 모의실험 환경은 수심 100 m 천해 환경으로 설정하였다. 해수면 음속이 1510 m/s 해저면 음속이 1500 m/s 로 선형음속구조 환경에서 직접파만을 고려하여 기뢰표적 반향신호의 수신 고각을 추정하고, 기뢰표적의 거리 및 수심 추정 알고리즘의 정확도를 비교하였다. 전방감시소나의 운용수심, 즉 송수신기 수심은 50 m 로 설정하였고, 기뢰표적의 수심은 계류기뢰를 가정하여 30 m, 80 m로 설정하였다.
Fig. 7은 설정한 해양환경에서 음선추적 결과를 나타낸다. 음파가 전파되면서 하향 굴절하는 환경임을 확인할 수 있다. 기뢰표적의 거리는 150 m부터 1 km 까지 50 m 간격으로 나누어 모의실험을 진행하였다. 측정 오차를 포함하기 위하여 송신신호 모의 시 송신 고각에 평균이 0, 분산이 1 도인 표준 정규분포를 따르는 노이즈를 추가하여 표적의 거리별 100회의 몬테칼로(Monte‑Carlo) 시뮬레이션을 수행하여 제안한 방법의 성능을 확인하였다. Fig. 8은 기뢰표적의 수심이 30 m, 80 m 일 때 거리별 수신 고각을 추정한 결과로 100번의 몬테칼로 시뮬레 이션을 통하여 구해진 거리별 수신 고각의 평균추정 값을 나타낸다. 참 값에 해당하는 표적신호 수신 고각과 추정한 수신 고각 값의 큰 차이가 존재하지 않으며, 기뢰표적의 거리가 점점 멀어지더라도 좋은 추정 결과를 보인다.
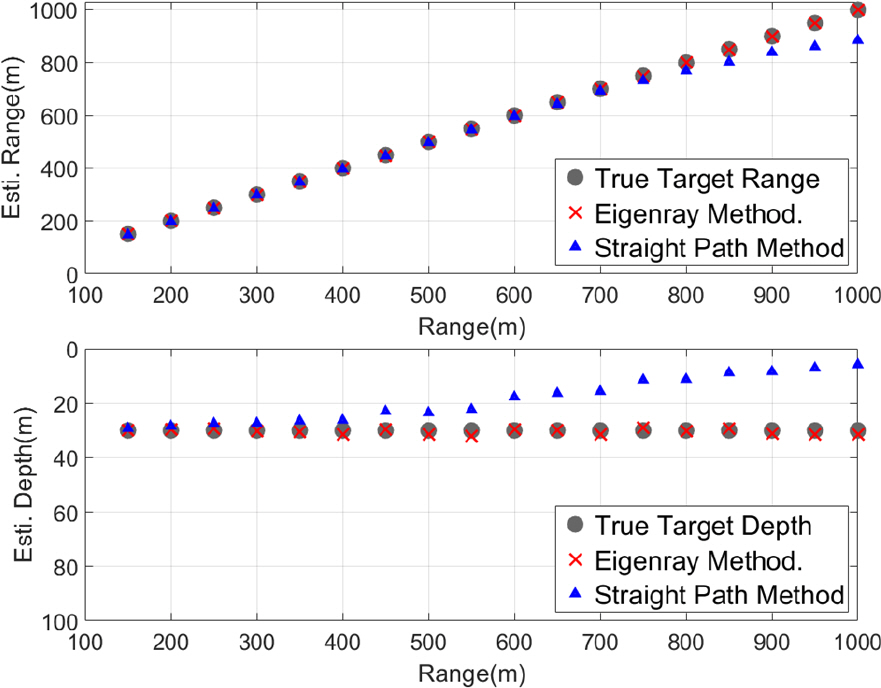
Fig. 9는 기뢰 표적의 수심이 30 m, Fig. 10은 기뢰 표적의 수심이 80 m 일 때거리별로 직선 경로를 가정하여 기뢰의 거리(위) 및 수심(아래)을 추정한 결과와 고유음선 추적을 통하여 추정한 결과를 나타낸다. Fig. 7과 마찬가지로 100 번의 몬테칼로 시뮬레이션을 통하여 구해진 거리별 위치 추정 값의 평균 추정값을 나타낸다. 표적의 수심이 30 m 결과에서 거리가 멀어질수록 거리 추정 시 직선경로를 가정한 추정방법의 오차가 발생함을 보이며 이는 직선경로 가정 시 모의 환경의 해수면 부근 음속이 빨라짐을 반영하지 못하여 생기는 오차이다. Fig. 9와 Fig. 10의 수심추정 오차 그래프에서 직선으로 가정하여 수심을 추정한 방법이 거리가 멀어질수록 표적수심보다 얕은 수심을 추정하는 경향이 나타난다. 이는 3.2절에 기술하였듯이, 음파가 하향 굴절하는 환경이라 음파가 도달하는 수신 고각이 실제 표적 위치의 고각보다 해수면 방향고각으로 추정된다. 수신 고각을 이용하여 직선으로 추정하게 되면 실제 표적의 수심보다 얕은 수심으로 추정될 수 밖에 없다. 따라서 음파의 굴절을 고려하지 않고 직선으로 기뢰위치를 추정한다면, Fig. 6과 같이 거리가 멀어질수록 굴절에 의한 오차의 크기가 증가한다. 따라서 음파의 전달경로를 직선 경로로 가정하였을 때 음파의 굴절효과를 반영하지 못하므로 음선추적 방법을 이용하였을 경우 기뢰표적의 거리 및 수심 추정의 정확성을 높일 수 있었다.
잠수함에서 전방을 탐색하기 위하여 전방주시소나를 사용하며, 복잡한 수중 환경에서 잠수함의 생존성을 보장하기 위하여 기뢰탐지 기법의 정확성이 중요시 된다. 이에 본 논문에서는 전방주시소나를 이용하여 전방주시소나의 원시 데이터를 모의하고 기뢰표적 반향신호를 모의하였다. 이후 모의된 기뢰표적 반향신호를 이용하여 음파의 굴절효과를 반영한 기뢰표적 위치를 추정하는 방법을 제안하였다. 모의실험을 통하여 음속구조를 반영한 환경에서 표적위치 추정결과가 좋은 추정 값을 보이는 것을 확인하였다. 본 연구에서 제안하는 표적 위치추정 기법은 거리 및 수심을 동시에 추정할 수 있어 효과적인 방법으로 사용될 수 있다고 판단된다.
Fig. 11은 다중경로를 고려한 환경에서 기뢰표적의 수심이 30 m 일 때 거리별 표적신호의 수신 고각을 추정한 결과이다. 표적신호의 수신 고각 추정 시 직접파만 고려한 환경보다 표적의 거리가 멀어질수록 추정 오차가 커짐을 보이며, 이는 LFM 송신신호의 시간분해능보다 짧은 시간 내 여러 경로의 표적신호가 수신되면서 직접경로의 수신준위를 정확히 탐지하지 못하여 수신 고각 추정결과에 오차를 야기하는 것으로 판단된다. 위의 결과는 음파의 반사만을 고려하여 다중경로가 모의되었지만 실제 해양에서 음파는 많은 경로에서 산란을 거치며 잔향음이 발생하고 표적 탐지의 제한 요소로 작용된다. 따라서 다중경로 환경을 반영한 기뢰탐지를 고려하기 위해서는 추후 잔향음까지 고려된 기뢰탐지에 대한 연구가 필요하며, 실제 해양환경에서 실측된 신호를 이용하여 제안된 알고리즘의 검증이 추가적으로 요구된다. 본 논문에서는 방위에 대한 고려는 제외된 기뢰 표적의 거리 및 수심을 추정 기법을 제안하였으며, 향후 전방주시소나의 수평배열 수신센서를 고려하여 기뢰표적의 거리, 수심, 방위추정 기법으로 확장 가능성이 존재한다.
References
[1] T. Yoo, S. Park, S. Yoon and H. Park, "Analysis of the Effectiveness of Autonomous Unmanned Underwater Vehicle Mine Search Operation by Side Scan Sonar Characteristics," Journal of the Korea Institute of Information and Communication Engineering, Vol. 24, No. 8, pp. 1077–1085, 2020.
[2] F. Ferreira, V. Djapic, M. Micheli and M. Caccia, "Forward Looking Sonar Mosaicing for Mine Countermeasures," Annual Reviews in Control, Vol. 40, pp. 212–226, 2015.

[3] N. Palomeras, T. Furfaro, D. P. Williams, M. Carreras and S. Dugelay, Automatic Target Recognition for Mine Countermeasure Missions Using Forward-Looking Sonar Data, in IEEE Journal of Oceanic Engineering, pp.pp. 1–40, 2021.
[4] Y. oh, S. Park, Y. Kim, D. Park and B. Lee, "Multi Channel Sonar Signal Algorithm and Board Development For High Speed Forward 3D Looking Sonar," Journal of Advanced Marine Engineering and Technology, Vol. 4, pp. 363–364, 2010.
[5] N. Hurtós, D. Ribas, X. Cufí, Y. Petillot and J. Salvi, "Fourier-based Registration for Robust Forward-Looking Sonar Mosaicing in Low-Visibility Underwater Environments," Journel of Field Robotics, Vol. 32, No. 1, pp. 123–151, 2015.

[6] A. B. Braggeroer, W. A. Kuperman and H. Schmidt, "Matched Field Processing: Source Localization in Correlated Noise as an Optimumparameter Estimation Problem," The Journal of the Acoustical Society of America, Vol. 83, No. 2, pp. 571–587, 1988.

[7] G. L. D'Spain, W. S. Hodgkiss and J. J. Murray, "Analytical and Experimental Comparison of Azimuth/Range/Depth Bias Errors in MFP Source Localization Using Vertical and Tilted Arrays," The Journal of the Acoustical Society of America, Vol. 101, No. 5, pp. 3047–3048, 1997.

[8] Brian M. Worthmann, H. C. Song and David R. Dowling, "Adaptive Frequency-Difference Matched Field Processing for High Frequency Source Localization in a Noisy Shallow Ocean," The Journal of the Acoustical Society of America, Vol. 141, No. 1, pp. 543–556, 2017.


[9] D. J. Geroski and D. R. Dowling, "Long-Range Frequency-Difference Source Localization in the Philippine Sea," The Journal of the Acoustical Society of America, Vol. 146, No. 6, pp. 4727–4739, 2019.


[10] P. A. Forero and P. Baxley, "Compressive Sensing Methods for Passive Localization and Tracking of Undersea Acoustic Sources," The Journal of the Acoustical Society of America, Vol. 140, pp. 31172016.

[11] S-Y. Kim, K-M. Kim, S-Y. Chum and B-I. Kim, "Range Estimating Performance Evaluation of the Underwater Broadband Source by Array Invariant," The Journal of the Acoustical Society of Korea, Vol. 25, No. 6, pp. 305–311, 2006.
[12] D. Kim, Y. Choi, J. Kim and J. Hahn ans J-S. Park, Depth Estimation in Active Sonar based on the Ray-Backpropagation, Joint Conference by KSNVE, ASK and KSME(DC). pp. 4512017.
[13] X. Lurton, "An Introduction to Underwater Acoustics : Principes and Applications," Springer, Germany, p. 244–255, 2002.
[14] G. M. Wenz, "Acoustic Ambient Noise in the Ocean : Spectra and Sources," The Journal of the Acoustical Society of America, Vol. 34, No. 12, pp. 1936–1956, 1962.

[15] M. B. Porter, "The BELLHOP Manual and User's Guide: PRELIMINARY DRAFT," Heat, Light, and Sound Research, Inc., USA, p. 1–57, 2011.
[16] F. B. Jensen, W. A. Kuperman, M. B. Porter and H. Schmidt, "Computational Ocean Acoustics," American Institute of Physics, USA, p. 36–38, 2011.
[17] R. J. Urick, "Principle of Underwater Sound," McGraw-Hill, USA, p. 291–295, 1983.
[18] P. Delos, B. Broughton and J. Kraft., "Phased Array Antenna Patterns - Part 1: Linear Array Beam Characteristics and Array Factor," Analog Dialogue, Vol. 54, No. 2, pp. 1–8, 2020.
- TOOLS
-
METRICS

-
- 0 Crossref
- 1,516 View
- 20 Download
- Related articles in J. KIMS Technol.
-
A Study on the Behavior of Skid Gear During the Helicopter Autorotation2012 December;15(6)