3.1 кіөк°„л¶„н• мқҳ лӘ©м Ғ
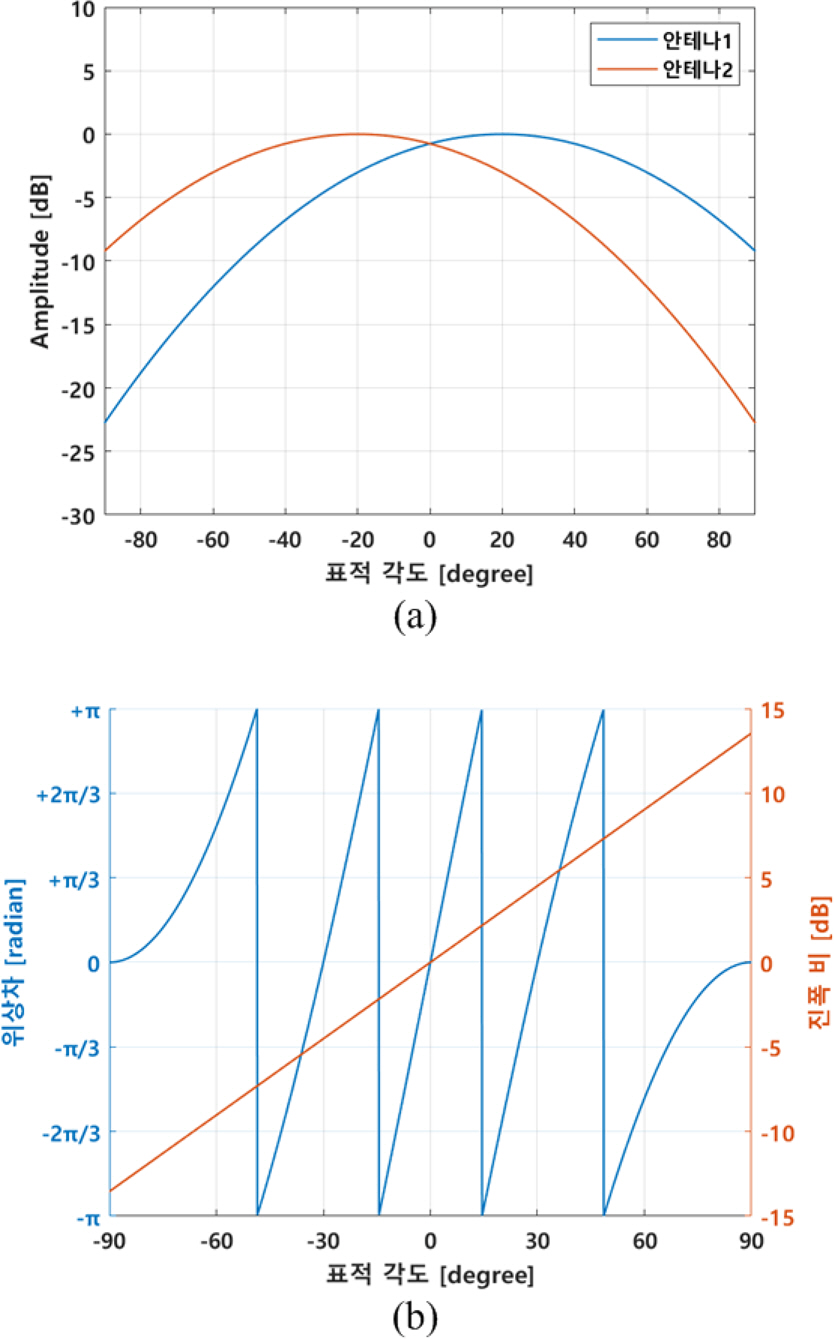
лӢЁмӣҗнҳ•л°°м—ҙм•Ҳн…ҢлӮҳлҘј м Ғмҡ©н•ң л°©н–Ҙнғҗм§Җ мӢңмҠӨн…ңмқҳ м •л°Җн•ң к°ҒлҸ„ 추м Ғмқ„ мң„н•ҙм„ңлҠ” л§Өмҡ° м •л°Җн•ң к°ҒлҸ„ 추м Ғ м •нҷ•лҸ„к°Җ н•„мҡ”н•ҳлҜҖлЎң, лӢЁмӣҗнҳ•л°°м—ҙм•Ҳн…ҢлӮҳлҘј м Ғмҡ©н•ң л°©н–Ҙнғҗм§Җ мӢңмҠӨн…ңмқҖ к°„м„ӯкі„ л°©мӢқмңјлЎң н‘ңм Ғмқҳ л°©н–Ҙнғҗм§Җ л°Ҹ 추м Ғмқ„ мҲҳн–үн•ҳлҠ” кІғмқҙ м Ғм Ҳн•ҳлӢӨ. н•ҳм§Җл§Ң мң„мқҳ 2мһҘм—җм„ң кё°мҲ н•ң л°”мҷҖ к°ҷмқҙ, к°„м„ӯкі„мқҳ мҡ°мҲҳн•ң к°ҒлҸ„ 추м Ғ м •нҷ•лҸ„ м„ұлҠҘмқ„ нҷңмҡ©н•ҳкё° мң„н•ҙм„ңлҠ” лӘЁнҳём„ұ л¬ём ңлҘј н•ҙкІ°н•ҙм•јл§Ң н•ңлӢӨ.
мқҙм—җ ліё л…јл¬ём—җм„ңлҠ” 진нҸӯ 비көҗ кё°лІ•кіј кіөк°„л¶„н• н…Ңмқҙлё”
[6]мқ„ мқҙмҡ©н•ҳм—¬ л°°м—ҙ м „л°© 3м°Ёмӣҗ кіөк°„мғҒм—җм„ң к°„м„ӯкі„ лӘЁнҳём„ұмқ„ м ңкұ°н•ҳкі мһҗ н•ңлӢӨ. 2мһҘм—җм„ң м–ёкёүн•ң л°”мҷҖ к°ҷмқҙ л°°м—ҙ м „л°© 3м°Ёмӣҗ кіөк°„мғҒм—җм„ңлҠ” н‘ңм Ғмқҳ л°©мң„к°Ғ/кі к°Ғкіј 진нҸӯ 비 мӮ¬мқҙм—җ лӢЁмҲңн•ң м„ нҳ• кҙҖкі„к°Җ м„ұлҰҪн•ҳм§Җ м•ҠмңјлҜҖлЎң, ліё л…јл¬ём—җм„ңлҠ” л°°м—ҙ м „л°©мқҳ кіөк°„мқ„ м—¬лҹ¬ к°ңмқҳ мҳҒм—ӯмңјлЎң л¶„н• н•ң нӣ„ 진нҸӯ 비лҘј мқҙмҡ©н•ҳм—¬ м–ҙлҠҗ мҳҒм—ӯм—җ н‘ңм Ғмқҙ мЎҙмһ¬н•ҳлҠ”м§ҖлҘј нҢҗлӢЁн•ҳлҠ” л°©м•Ҳмқ„ м ңм•Ҳн•ҳмҳҖлӢӨ. н‘ңм Ғмқҙ мЎҙмһ¬н•ҳлҠ” мҳҒм—ӯмқ„ м°ҫкі н•ҙлӢ№ мҳҒм—ӯ л°©н–ҘмңјлЎң л°©н–Ҙнғҗм§Җ мӢңмҠӨн…ңмқ„ нғ‘мһ¬н•ң 비н–үмІҙлҘј м§Җн–Ҙн•ҳлҠ” м Ҳм°ЁлҘј л°ҳліөм ҒмңјлЎң мҲҳн–үн•ЁмңјлЎңмҚЁ л°°м—ҙ кё°мӨҖл°©н–Ҙ л¶Җк·ј мҳҒм—ӯмңјлЎң н‘ңм Ғмқ„ мң„м№ҳмӢңнӮ¬ мҲҳ мһҲмңјл©°, мқҙлҠ” лӘЁнҳём„ұ л¬ём ңлҘј н•ҙкІ°н•ҳм—¬ к°„м„ӯкі„ л°©мӢқмңјлЎң н‘ңм Ғмқҳ л°©н–Ҙнғҗм§Җ л°Ҹ 추м Ғмқ„ мҲҳн–үн• мҲҳ мһҲкІҢ н•ңлӢӨ. мҳҲлҘј л“Өм–ҙ,
Fig. 2мҷҖ к°ҷмқҖ кІҪмҡ°, л°°м—ҙ кё°мӨҖл°©н–Ҙ(0В°)мқ„ мӨ‘мӢ¬мңјлЎң Вұ14.4В° мқҙлӮҙм—җ н‘ңм Ғмқҙ мң„м№ҳн•ҳкІҢ н•ҳл©ҙ к°„м„ӯкі„ м Ғмҡ© мӢң лӘЁнҳём„ұ л¬ём ңк°Җ л°ңмғқн•ҳм§Җ м•ҠкІҢ лҗңлӢӨ.
ліё л…јл¬ём—җм„ң м ңм•Ҳн•ҳлҠ” л°©н–Ҙнғҗм§Җ л°Ҹ 추м Ғ м•Ңкі лҰ¬мҰҳмқҖ
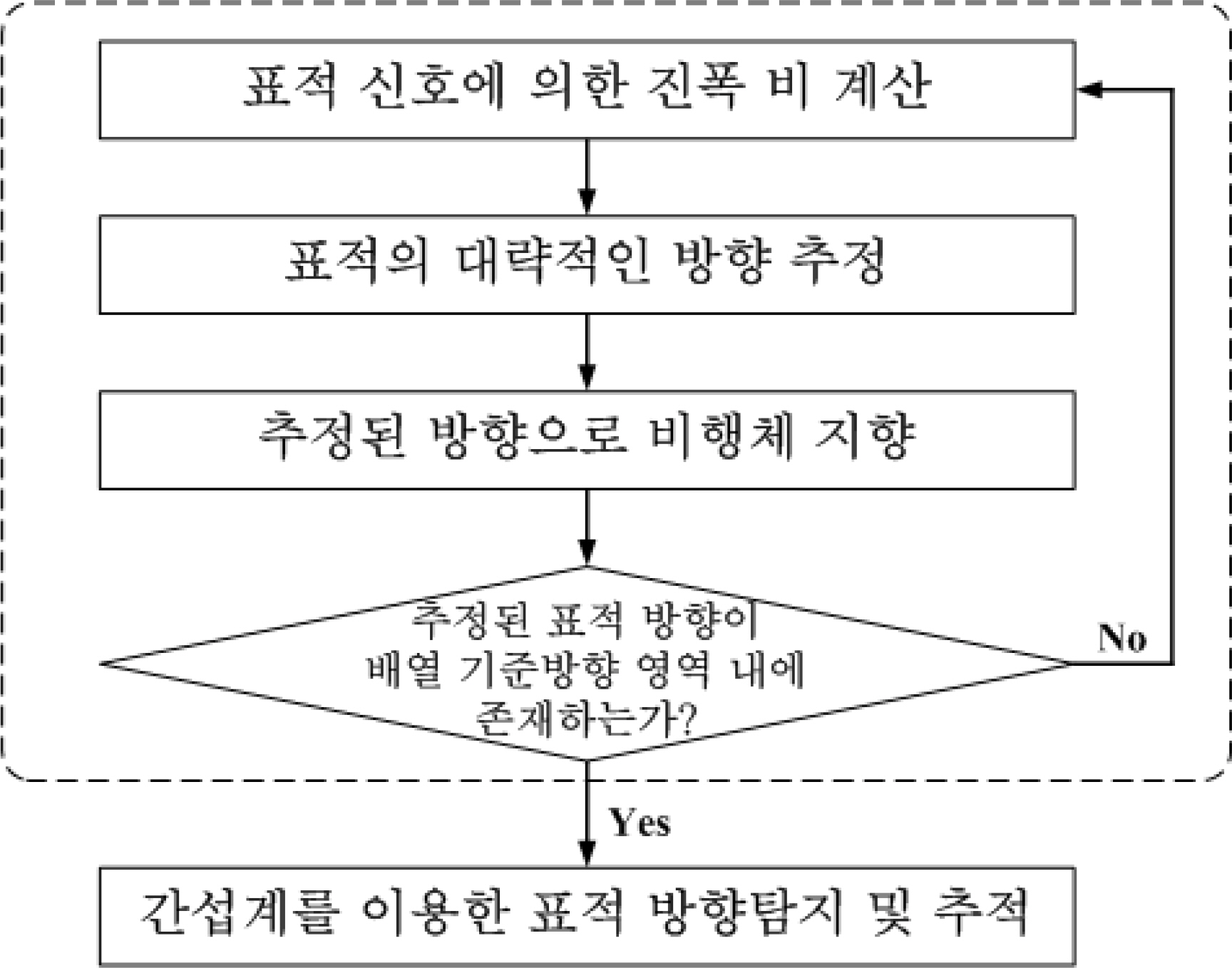
Fig. 4мҷҖ к°ҷмңјл©° мғҒм„ён•ң лӮҙмҡ©мқҖ мқҙнӣ„мқҳ м Ҳм—җм„ң кё°мҲ н•ңлӢӨ. ліё л…јл¬ём—җм„ң лӢӨлЈЁлҠ” лӮҙмҡ©мқҖ 진нҸӯ 비мҷҖ кіөк°„л¶„н• н…Ңмқҙлё”мқ„ мқҙмҡ©н•ҳм—¬ к°„м„ӯкі„ лӘЁнҳём„ұмқҙ мЎҙмһ¬н•ҳм§Җ м•ҠлҠ” л°°м—ҙ кё°мӨҖл°©н–Ҙ мҳҒм—ӯмңјлЎң н‘ңм Ғмқ„ мң„м№ҳмӢңнӮӨлҠ” л°©лІ•м—җ лҢҖн•ң кІғмңјлЎң
Fig. 4мқҳ м җм„ лӮҙл¶Җм—җ н•ҙлӢ№н•ңлӢӨ.
Fig.В 4.
Direction finding and tracking algorithm
3.2 кіөк°„л¶„н• кІ©мһҗ
Fig. 5мҷҖ к°ҷмқҙ л°°м—ҙ м „л°©мқҳ 3м°Ёмӣҗ кіөк°„мғҒм—җ л°°м—ҙмқҳ кё°мӨҖл°©н–Ҙкіј
ОёSD,m (
m = 1, вҖҰ,
M)мқҳ к°Ғмқ„ к°–лҠ” м җл“Өмқ„ м—°кІ°н•ң мӣҗлҝ”
О©mмқ„ мғқм„ұн•ңлӢӨ.
О©1 лӮҙл¶Җмқҳ мҳҒм—ӯмқ„ мІ« лІҲм§ё л¶„н• л ҲлІЁ,
О©mкіј
О©m-1 мӮ¬мқҙмқҳ мҳҒм—ӯмқ„
m лІҲм§ё л¶„н• л ҲлІЁмқҙлқј н•ҳкі , к°Ғ л ҲлІЁмқҳ нҒ¬кё°
dmмқ„ мӢқ (4)мҷҖ к°ҷмқҙ м •мқҳн•ңлӢӨ.
Fig.В 5.

мқҙ л•Ң, мІ« лІҲм§ё л¶„н• л ҲлІЁмқҳ нҒ¬кё° d1лҠ” л°°м—ҙ кё°мӨҖл°©н–Ҙ мҳҒм—ӯмқҳ нҒ¬кё°лҘј кІ°м •н•ҳлҜҖлЎң к°„м„ӯкі„ лӘЁнҳём„ұмқҙ л°ңмғқн•ҳм§Җ м•ҠлҠ” к°ҒлҸ„ лІ”мң„(Вұ Оёua)лҘј м°ёкі н•ҳм—¬ м •н•ҙм•јн•ңлӢӨ. л°°м—ҙ кё°мӨҖл°©н–Ҙмқ„ мӨ‘мӢ¬мңјлЎң Вұ Оёua мқҙлӮҙм—җм„ң лӘЁнҳём„ұмқҙ л°ңмғқн•ҳм§Җ м•ҠлҠ” кІҪмҡ° d1 = 0.8 Оёua м •лҸ„лЎң м„Өм •н•ңлӢӨ. лҳҗн•ң мғҒкё°н•ң л°ҳліөм Ғмқё н‘ңм Ғ мЎҙмһ¬ мҳҒм—ӯ нғҗмғү л°Ҹ 비н–үмІҙ м§Җн–Ҙ мһ‘м—…мқҳ нҡЁмңЁмқ„ н–ҘмғҒмӢңнӮӨкё° мң„н•ҳм—¬, л¶„н• л ҲлІЁ m мқҙ мҰқк°Җн• мҲҳлЎқ л¶„н• л ҲлІЁмқҳ нҒ¬кё° dmмқ„ м җм°Ё мҰқк°ҖмӢңнӮҙмңјлЎңмҚЁ л°°м—ҙ кё°мӨҖл°©н–Ҙм—җм„ң л©Җм–ҙм§ҲмҲҳлЎқ л¶„н• мҳҒм—ӯмқҳ нҒ¬кё°к°Җ м»Өм§ҖлҸ„лЎқ н•ңлӢӨ. мқҙ л•Ң, мғқм„ұлҗң л¶„н• мҳҒм—ӯмқҳ нҳ•нғңк°Җ м •мӮ¬к°Ғнҳ•м—җ к°Җк№қлҸ„лЎқ dmмқҳ мҰқк°ҖнҸӯмқ„ м •н•ҳлҠ” кІғмқҙ л°”лһҢм§Ғн•ҳлӢӨ.
л°°м—ҙмқҳ мӨ‘мӢ¬мқ„ мӣҗм җмңјлЎң н•ҳлҠ” л°ҳм§ҖлҰ„ 1мқҳ кө¬лҘј к°Җм •н•ҳкі , к·ё кө¬мҷҖ мӣҗлҝ” О©mмқҙ көҗм°Ён•ҳлҠ” мӣҗмқ„ Cmмқҙлқј н•ңлӢӨ. мӣҗ CmмқҖ 2ПҖsin ОёSD,mмқҳ л‘ҳл ҲлҘј к°Җм§Җл©°, мқҙлҘј N л“ұ분 н•ҳлҠ” м җл“Өмқҙ кіөк°„л¶„н• кІ©мһҗ кө¬м„ұмқ„ мң„н•ң кјӯ짓м җл“Өмқҙ лҗңлӢӨ. мқҙ л•Ң, мӣҗ мң„мқҳ м җ мӮ¬мқҙмқҳ к°„кІ©мқ„ л¶„н• л ҲлІЁмқҳ нҒ¬кё°мҷҖ 비көҗн•ҳм—¬ м•„лһҳмқҳ мӢқ (5)лҘј л§ҢмЎұн•ҳлҠ” кІҪмҡ°, мӣҗмқ„ 2N л“ұ분н•ҳм—¬ кјӯ짓м җл“Өмқ„ мғқм„ұн•ЁмңјлЎңмҚЁ л¶„н• мҳҒм—ӯ к°„мқҳ нҒ¬кё° нҺём°ЁлҘј мӨ„мқҙлҸ„лЎқ н•ңлӢӨ.
мғҒкё°н•ң ліҖмҲҳл“Өмқ„ мЎ°м Ҳн•ЁмңјлЎңмҚЁ мһ„мқҳмқҳ кіөк°„л¶„н• кІ©мһҗлҘј кө¬м„ұн• мҲҳ мһҲмңјл©°, ліё л…јл¬ём—җм„ңлҠ” мғҒкё°н•ң ліҖмҲҳл“Өмқ„
M = 8,
N = 8,
ОёSD,1 = 6В°,
ОёSD,2 = 12В°,
ОёSD,3 = 20В°,
ОёSD,4 = 30В°,
ОёSD,5 = 42В°,
ОёSD,6 = 56В°,
ОёSD,7 = 72В°,
ОёSD,8 = 90В°лЎң м„Өм •н•ҳм—¬
Fig. 6кіј к°ҷмқҖ кіөк°„л¶„н• кІ©мһҗлҘј кө¬м„ұн•ҳмҳҖлӢӨ.
Fig.В 6.
Space division grids (M = 8, N = 8)
3.3 кіөк°„л¶„н• н…Ңмқҙлё”
м„ӨлӘ…мқҳ нҺёмқҳлҘј мң„н•ҳм—¬
Fig. 6м—җлҠ” л„Ө к°ңмқҳ м•Ҳн…ҢлӮҳлҘј л°°м—ҙн•ҳм—¬ л‘җ к°ңмқҳ 진нҸӯ 비көҗ 축(R/L축, U/D축)л§Ңмқ„ лӮҳнғҖлӮҙм—ҲмңјлӮҳ, л°©н–Ҙнғҗм§Җ м„ұлҠҘ н–ҘмғҒмқ„ мң„н•ҙ м•Ҳн…ҢлӮҳлҘј 추к°Җн•ҳм—¬ 진нҸӯ 비көҗ 축мқҳ мҲҳ(
K)лҘј мҰқк°ҖмӢңнӮ¬ мҲҳ мһҲлӢӨ. мқҙ л•Ң, л¶„н• мҳҒм—ӯмқҳ мҲҳлҠ” 진нҸӯ 비көҗ 축мқҳ к°ңмҲҳмҷҖлҠ” кҙҖкі„м—Ҷмқҙ мғҒкё°н•ң
M,
Nмқҳ к°’м—җ л”°лқјм„ңл§Ң кІ°м •лҗңлӢӨ.
Fig. 7мқҖ RU/LD축과 LU/RD축мқҙ 추к°Җлҗҳм–ҙ л„Ө к°ңмқҳ 진нҸӯ 비көҗ 축мқ„ к°–лҠ” кІҪмҡ°лҘј лӮҳнғҖлӮёлӢӨ.
Fig.В 7.

н‘ңм Ғ мӢ нҳёмқҳ нҠ№м„ұ лІЎн„° TвҶ’мҷҖ jлІҲм§ё л¶„н• мҳҒм—ӯмқҳ нҠ№м„ұ лІЎн„° RjвҶ’лҠ” к°Ғк°Ғ мӢқ (6)кіј (7)лЎң м •мқҳн•ңлӢӨ.
м—¬кё°м„ң, tiлҠ” н‘ңм Ғ мӢ нҳём—җ мқҳн•ң iлІҲм§ё 진нҸӯ 비көҗ 축мқҳ dB лӢЁмң„ 진нҸӯ 비лҘј мқҳлҜён•ңлӢӨ. ri,jлҠ” jлІҲм§ё л¶„н• мҳҒм—ӯм—җ лҢҖн•ң iлІҲм§ё 진нҸӯ 비көҗ 축мқҳ dB лӢЁмң„ 진нҸӯ 비лҘј мқҳлҜён•ҳл©°, ri,jм—җ лҢҖн•ң мғҒм„ён•ң м„ӨлӘ…мқҖ 3.3.1 ~ 3.3.3м Ҳм—җ кё°мҲ н•ңлӢӨ.
н‘ңм Ғ мӢ нҳёмқҳ нҠ№м„ұ лІЎн„° TвҶ’мҷҖ л¶„н• мҳҒм—ӯмқҳ нҠ№м„ұ лІЎн„° RjвҶ’к°Җ мң мӮ¬н• мҲҳлЎқ н‘ңм Ғмқҙ н•ҙлӢ№ л¶„н• мҳҒм—ӯ лӮҙм—җ мЎҙмһ¬н• нҷ•лҘ мқҙ лҶ’мңјлҜҖлЎң, мӢқ (8)мқ„ мқҙмҡ©н•ҳм—¬ л‘җ лІЎн„° TвҶ’мҷҖ RjвҶ’к°„мқҳ кұ°лҰ¬к°Җ мөңмҶҢк°Җ лҗҳлҠ” л¶„н• мҳҒм—ӯ лӮҙм—җ н‘ңм Ғмқҙ мЎҙмһ¬н• к°ҖлҠҘм„ұмқҙ к°ҖмһҘ нҒ¬л©°, мөңмҶҢн•ң мӢӨм ң н‘ңм Ғмқҙ мЎҙмһ¬н•ҳлҠ” л¶„н• мҳҒм—ӯм—җ мқём ‘н•ң л¶„н• мҳҒм—ӯ лӮҙм—җлҠ” н‘ңм Ғмқҙ мң„м№ҳн•ңлӢӨкі нҢҗлӢЁн• мҲҳ мһҲлӢӨ.
н‘ңм Ғмқҙ мЎҙмһ¬н• кІғмңјлЎң мҳҲмғҒлҗҳлҠ” л¶„н• мҳҒм—ӯмқ„ кІ°м •н•ҳл©ҙ, н•ҙлӢ№ л¶„н• мҳҒм—ӯмқҳ л°©н–Ҙ лІЎн„° DjвҶ’ л°©н–Ҙм—җ н‘ңм Ғмқҙ мң„м№ҳн•ңлӢӨкі м¶”м •н•ҳкі л№„н–үмІҙлҘј DjвҶ’ л°©н–ҘмңјлЎң м§Җн–Ҙн•ңлӢӨ. л¶„н• мҳҒм—ӯмқҳ л°©н–Ҙ лІЎн„° DjвҶ’лҠ” л¶„н• мҳҒм—ӯмқ„ кө¬м„ұн•ҳлҠ” кјӯ짓м җмқҳ л°©н–Ҙ лІЎн„°л“Өмқҳ лІЎн„° н•©мңјлЎң кі„мӮ°н•ҳл©°, jлІҲм§ё л¶„н• мҳҒм—ӯмқҙ Pa, Pb, ..., Pzмқҳ кјӯ짓м җмңјлЎң кө¬м„ұлҗң кІҪмҡ° DjвҶ’лҠ” мӢқ (9)мҷҖ к°ҷлӢӨ.
мӢӨм ң н‘ңм Ғмқҳ л°©н–Ҙкіј м¶”м • л°©н–Ҙ DjвҶ’ к°„м—җлҠ” л¶„н• мҳҒм—ӯмқҳ нҒ¬кё°м—җ 비лЎҖн•ҳлҠ” мҳӨм°Ёк°Җ мЎҙмһ¬н•ңлӢӨ. н•ҳм§Җл§Ң л°°м—ҙ кё°мӨҖл°©н–Ҙкіј к°Җк№ҢмҡёмҲҳлЎқ л¶„н• мҳҒм—ӯмқҳ нҒ¬кё°к°Җ мһ‘м•„м§ҖлҜҖлЎң, л°ҳліөм ҒмңјлЎң мғҒкё°н•ң л¶„н• мҳҒм—ӯ нғҗмғү л°Ҹ 비н–үмІҙ м§Җн–Ҙ кіјм •мқ„ мҲҳн–үн•ҳл©ҙ м җм°Ё л°°м—ҙ кё°мӨҖл°©н–Ҙ л¶Җк·јмңјлЎң н‘ңм Ғмқҙ мқҙлҸҷн•ҳкІҢ лҗҳл©°, мөңмў…м ҒмңјлЎңлҠ” л°°м—ҙ кё°мӨҖл°©н–Ҙ мҳҒм—ӯ лӮҙм—җ н‘ңм Ғмқҙ мң„м№ҳн•ҳкІҢ лҗңлӢӨ.
мӢӨм ң л°©н–Ҙнғҗм§Җ мӢңмҠӨн…ң м Ғмҡ© мӢңм—җлҠ”, кіөк°„л¶„н• кІ©мһҗ кө¬м„ұ нӣ„ к°Ғ л¶„н• мҳҒм—ӯмқҳ л°©н–ҘлІЎн„°лҘј кө¬н•ҳкі лӢЁмӣҗнҳ•л°°м—ҙм•Ҳн…ҢлӮҳ м ңмһ‘ нӣ„ мёЎм •мқ„ нҶөн•ҙ к°Ғ л¶„н• мҳҒм—ӯмқҳ нҠ№м„ұ лІЎн„°лҘј кө¬н•ҳм—¬ м•„лһҳ
Table 1кіј к°ҷмқҖ кіөк°„л¶„н• н…Ңмқҙлё”мқ„ мғқм„ұн•ңлӢӨ. мғқм„ұлҗң кіөк°„л¶„н• н…Ңмқҙлё”мқ„ мӮ¬м „м—җ л°©н–Ҙнғҗм§Җ мӢңмҠӨн…ңм—җ мһҘмһ…н•ң нӣ„ мӢӨм ң мҡҙмҡ© мӢң мқҙлҘј нҷңмҡ©н•ЁмңјлЎңмҚЁ н‘ңм Ғм—җ лҢҖн•ң л°©н–Ҙнғҗм§Җ л°Ҹ 추м Ғмқ„ мҲҳн–үн•ҳкІҢ лҗңлӢӨ.
TableВ 1.
Space division table (M = 8, N = 8 case)
|
л¶„н• мҳҒм—ӯ |
л°©н–Ҙ лІЎн„° |
нҠ№м„ұ лІЎн„° |
|
1 |
D1вҶ’
|
R1вҶ’вҖү=[r1,1,вҖүr2,1,вҖҰ,вҖүrK,вҖү1]
|
|
2 |
D2вҶ’
|
R2вҶ’вҖү=[r1,2,вҖүr2,2,вҖҰ,вҖүrK,вҖү2]
|
|
вӢ® |
вӢ® |
вӢ® |
|
89 |
D89вҶ’
|
R89вҶ’вҖү=[r1,89,вҖүr2,89,вҖҰ,вҖүrK,вҖү89]
|
л¶„н• мҳҒм—ӯмқҖ мҳҒм—ӯмқ„ кө¬м„ұн•ҳлҠ” кјӯ짓м җмқҳ мҲҳ, Zм—җ л”°лқј л°°м—ҙ кё°мӨҖл°©н–Ҙ мҳҒм—ӯ(Z = N), мқјл°ҳ мҳҒм—ӯ(Z = 4), мһ¬л¶„н• л°ңмғқ мҳҒм—ӯ(Z = 5)мқҳ м„ё к°Җм§ҖлЎң кө¬л¶„н• мҲҳ мһҲмңјл©°, к°Ғ мҳҒм—ӯм—җ лҢҖн•ң мғҒм„ён•ң м„ӨлӘ…кіј RjвҶ’ кі„мӮ° л°©лІ•мқҖ м•„лһҳм—җ кё°мҲ н•ңлӢӨ.
3.3.1 л°°м—ҙ кё°мӨҖл°©н–Ҙ мҳҒм—ӯ
л°°м—ҙ кё°мӨҖл°©н–Ҙ мҳҒм—ӯмқҖ кіөк°„л¶„н• н…Ңмқҙлё”мқҳ 1лІҲ л¶„н• мҳҒм—ӯмңјлЎңм„ң, мқҙ мҳҒм—ӯ лӮҙм—җ н‘ңм Ғмқҙ мң„м№ҳн• кІҪмҡ° к°„м„ӯкі„ лӘЁнҳём„ұ л¬ём ңк°Җ л°ңмғқн•ҳм§Җ м•ҠлҠ”лӢӨ. л°°м—ҙ кё°мӨҖл°©н–Ҙм—җм„ңлҠ” 진нҸӯ 비көҗ 축м—җ кҙҖкі„м—Ҷмқҙ 0 dBмқҳ 진нҸӯ 비 к°’мқ„ к°Җм§ҖлҜҖлЎң, мғҒкё°н•ң мӢқ (7)мқҳ ri,1мқҖ лӢӨмқҢкіј к°ҷлӢӨ.
3.3.2 мқјл°ҳ мҳҒм—ӯ
кіөк°„л¶„н• кІ©мһҗлЎң л¶„н• лҗҳлҠ” лҢҖл¶Җ분мқҳ мҳҒм—ӯмқҖ л„Ө к°ңмқҳ кјӯ짓м җмңјлЎң кө¬м„ұлҗң мқјл°ҳ мҳҒм—ӯмқҙлӢӨ. мқјл°ҳмҳҒм—ӯмқҳ кІҪмҡ°, мҳҒм—ӯмқ„ кө¬м„ұн•ҳлҠ” л„Ө кјӯ짓м җм—җм„ңмқҳ 진нҸӯ 비лҘј мқҙмҡ©н•ҳм—¬ л¶„н• мҳҒм—ӯмқҳ нҠ№м„ұ лІЎн„° RjвҶ’лҘј кі„мӮ°н•ңлӢӨ.
н‘ңм Ғмқҙ PaвҶ’ л°©н–Ҙм—җ мЎҙмһ¬н• л•Ң iлІҲм§ё 진нҸӯ 비көҗ 축мқҳ dB лӢЁмң„ 진нҸӯ 비лҘј ai,a(i = 1, вҖҰ, K)лқј н•ҳкі , jлІҲм§ё л¶„н• мҳҒм—ӯмқ„ кө¬м„ұн•ҳлҠ” л„Ө кјӯм§Җм җмқ„ Pa, Pb, Pc, Pdлқј н•ҳл©ҙ, мғҒкё°н•ң мӢқ (7)мқҳ ri,jлҠ” м•„лһҳмқҳ мӢқ (11)лЎң кі„мӮ°н•ңлӢӨ.
мҳҲлҘј л“Өм–ҙ,
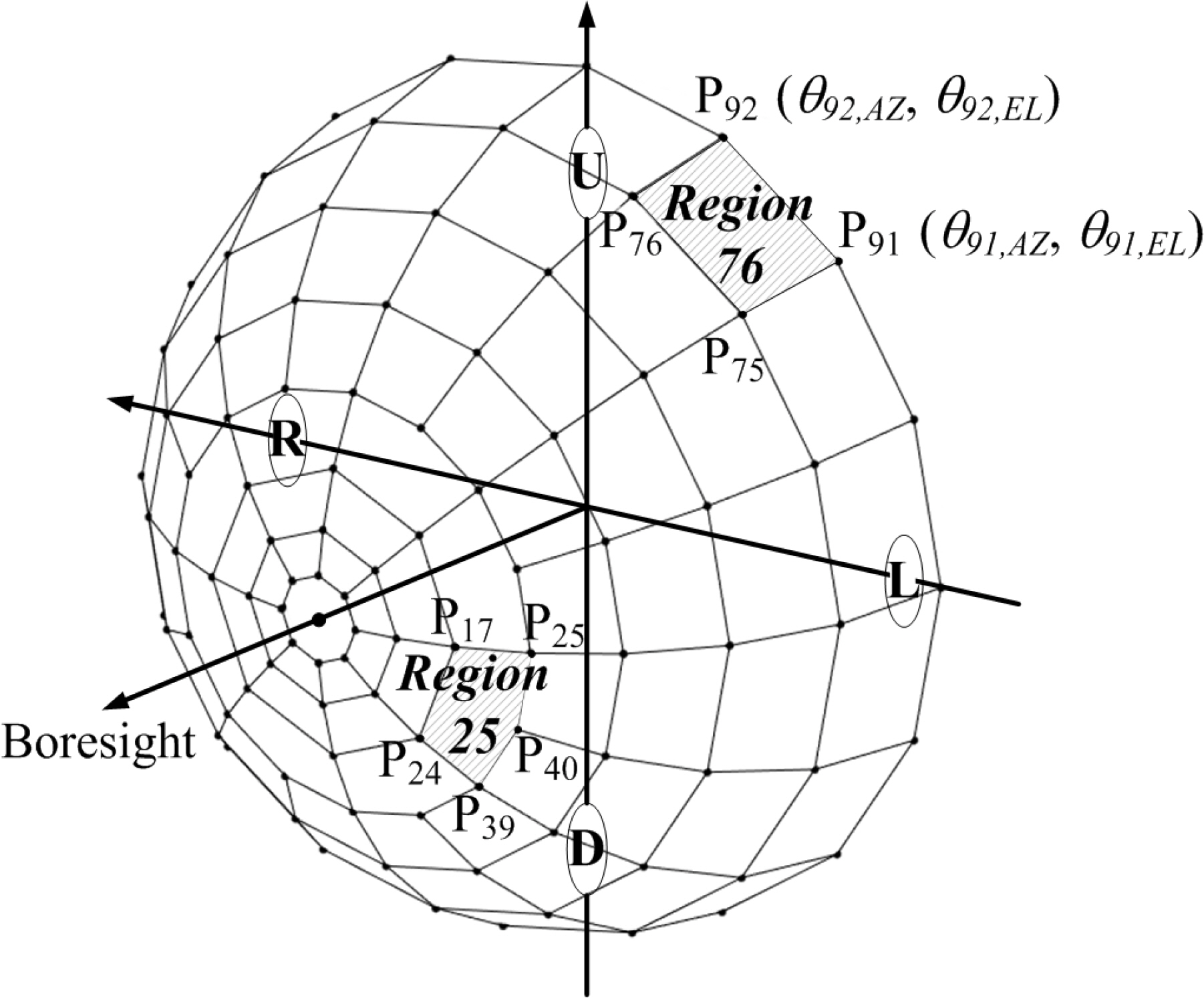
Fig. 6кіј к°ҷмқҙ л‘җ к°ңмқҳ 진нҸӯ 비көҗ 축(R/L 축, U/D축)мқҙ мЎҙмһ¬н•ҳлҠ” кІҪмҡ°, мІ« лІҲм§ё 진нҸӯ 비көҗ 축мқ„ R/L축, л‘җ лІҲм§ё 진нҸӯ 비көҗ 축мқ„ U/D축мқҙлқј н•ҳл©ҙ, P
75вҖ’P
76вҖ’P
91вҖ’P
92лЎң кө¬м„ұлҗҳлҠ” мқјл°ҳ мҳҒм—ӯмқҳ нҠ№м„ұ лІЎн„°
R76вҶ’лҠ”
[a1.75+a1.76+a1,91+a1,924,вҖүa2,75+a2,76+a2,91+a2,924] мҷҖ к°ҷлӢӨ.
3.3.3 мһ¬л¶„н• л°ңмғқ мҳҒм—ӯ
мғҒкё°н•ң л°”мҷҖ к°ҷмқҙ мӢқ (5)лҘј л§ҢмЎұн•ҳлҠ” кІҪмҡ°, кіөк°„л¶„н• кІ©мһҗ кө¬м„ұмқ„ мң„н•ң кјӯ짓м җ мғқм„ұ л°©лІ•мқҙ лӢ¬лқјм§җмңјлЎң мқён•ҳм—¬
Fig. 6мқҳ 25лІҲ мҳҒм—ӯкіј к°ҷмқҙ лӢӨм„Ҝ к°ңмқҳ кјӯ짓м җмңјлЎң кө¬м„ұлҗҳлҠ” л¶„н• мҳҒм—ӯмқҙ л°ңмғқн•ҳкІҢ лҗңлӢӨ. мқҙ л•Ң, лӢӨм„Ҝ к°ң кјӯ짓м җмқҳ 진нҸӯ 비лҘј лӘЁл‘җ мқҙмҡ©н•ҳм—¬ нҠ№м„ұ лІЎн„°лҘј кі„мӮ°н•ҳл©ҙ л°°м—ҙ кё°мӨҖл°©н–Ҙкіј лЁј мӘҪмңјлЎң нҠ№м„ұ лІЎн„°м—җ м№ҳмҡ°м№Ёмқҙ мЎҙмһ¬н• мҲҳ мһҲмңјлҜҖлЎң мҳҒм—ӯ мҷёкіҪмқҳ л„Ө к°ң кјӯ짓м җл§Ңмқ„ мқҙмҡ©н•ҳм—¬ нҠ№м„ұ лІЎн„°лҘј кі„мӮ°н•ңлӢӨ. мҳҲлҘј л“Өм–ҙ,
Fig. 6мқҳ кІҪмҡ°, P
17вҖ’P
24вҖ’P
25вҖ’P
39вҖ’P
40лЎң кө¬м„ұлҗҳлҠ” мһ¬л¶„н• л°ңмғқ мҳҒм—ӯмқҳ нҠ№м„ұ лІЎн„°
R25вҶ’лҠ” м•„лһҳмҷҖ к°ҷлӢӨ.